Примеры решения задач

Пример 1. Два одинаковых положительных точечных заряда находятся на расстоянии 2L = 10 см друг от друга. Найти на прямой МN (см. схему), являющейся осью симметрии этих зарядов, точку, в которой напряженность электрического поля имеет максимум.

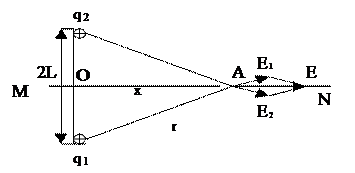Решение. Напряженность 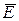электрического поля в любой точке прямой МN складывается из напряженносте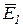й и 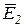, созданных в этой точке зарядами q₁ и q₂:

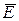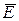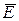= ₁ + ₂.

При этом в точке О, лежащей между зарядами, сумма векторов 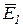и 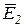, одинаковыхпо модулю и противоположных по направлению, равна нулю.

Найдем напряженность поля 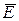в произвольной точке А прямой МN. Как видно из схемы,

Е = 2Е₁ cos φ, (1)

где j – угол между 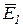и осью МN. Обозначив отрезок ОА через х и учитывая соотношения

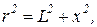
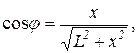
вместо равенства (1) на основании формулы для напряженности электрического поля, созданного точечным зарядом,

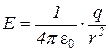
получим

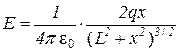. (2)

Эта формула выражает модуль вектора 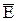в произвольной точке прямой МN как функцию координаты х этой точки. Чтобы найти максимум функции, продифференцируем ее по х и приравняем нулю производную:

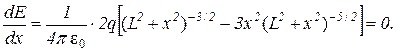
Отсюда находим

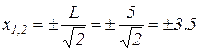см.

Два значения х соответствуют двум точкам, расположенным по обе стороны от точки О на расстоянии 3.5 см от нее.

Пример 2. Определить потенциал электрического поля точечного диполя, электрический момент которого р=2 × 10^-14 Кл × м, в точке, лежащей на оси диполя на расстоянии 0.10 м от его центра со стороны положительного заряда.

Решение. Из принципа суперпозиции полей следует, что потенциал любой точки электрического поля равен алгебраической сумме потенциалов, созданных в этой точке каждым зарядом диполя:

φ = φ₊ + φ_– .

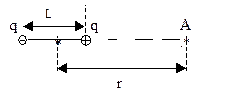Тогда для точки А (см. схему) по формуле потенциала поля точечного заряда на расстоянии R от него

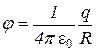
имеем

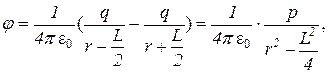
где (p = q × L) – момент диполя; L – плечо диполя.

Для точечного диполя выполняется соотношение L<<r. Поэтому пренебрегая величиной (L²/4) в знаменателе, найдем

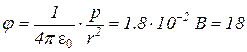мВ.

Пример 3. Плоский конденсатор с расстоянием между пластинами 1 см заряжен до разности потенциалов 1000 В. Определить объемную плотность энергии поля конденсатора. Диэлектрик – стекло.

Решение. Объемная плотность энергии поля конденсатора есть энергия, заключенная в единице объема поля, и может быть определена по формуле

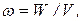
где W – энергия поля конденсатора; V – объем, занимаемый полем, т. е. объем пространства, заключенного между пластинами конденсатора.

Энергия поля конденсатора определяется по формуле

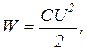
где C – емкость конденсатора; U – разность потенциалов, до которой заряжены пластины конденсатора.

В системе СИ

,

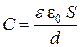V = Sd.

Подставив выражение C в W и затем выражения W и V – в ω, получим

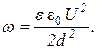
Переведем значения всех величин в систему СИ:

d = 1 см = 10^-2 м;

U = 10³ B;

ε = 7;

ε₀ = 8.85·10^-12 Ф/м.

Подставив эти значения в ω, произведем вычисления:

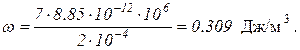
Пример 4. Пространство внутри плоского конденсатора заполнено двумя слоями диэлектриков, расположенными параллельно его обкладкам. Толщина слоев и диэлектрическая проницаемость материалов, из которых сделаны слои, соответственно равны L₁, L₂, ε₁, ε₂. Конденсатор заряжен до разности потенциалов U. Определить напряженности Е₁, Е₂ электрического поля в каждом из диэлектриков, а также напряженность Е₀ поля в зазоре между обкладками и диэлектриками.

Решение. Чтобы найти величинынапряженности Е₁, Е₂ и Е₀, выясним связь, существующую между ними и разностью потенциалов U. Известно, что разность потенциалов и напряженность электрического поля связаны соотношением

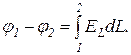(1)

Разбив весь путь интегрирования на две части, соответствующие толщинам двух слоев диэлектриков (толщиной зазора пренебрегаем), и учитывая, что в пределах каждого слоя поле однородно, получим

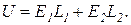(2)

Так как электрическое смещение D и в зазоре (ε = 1), и в обоих слоях диэлектриков имеет одно и то же значение, то на основании формулы

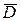= ε₀ ε 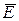, (3)

где ε – диэлектрическая проницаемость среды, сокращая на ε₀, запишем

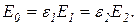(4)

Решая совместно уравнения (2) и (4), получим

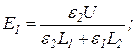
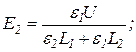
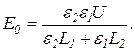
Пример 5. Элементы ε₁, ε₂ включены в цепь, как показано на схеме. Определить силы токов, текущих в сопротивлениях R₂ и R₃, если ε₁=10 В и ε₂=4 В, а R₁ = R₄ = 2 Ом и R₂ = R₃ = 4 Ом. Сопротивлениями элементов пренебречь.

Решение. Силы токов разветвленной цепи можно определить с помощью законов Кирхгофа. Перед составлением уравнений по законам Кирхгофа необходимо, во-первых, выбрать произвольно направления токов, текущих через сопротивления, и, во-вторых, выбрать направление обхода контуров. Выберем направления токов, как показано на схеме, и условимся обходить контуры по часовой стрелке.

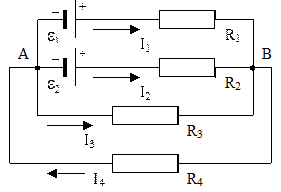Рассматриваемая в задаче схема имеет два узла А и В. Но составлять уравнение по первому закону Кирхгофа следует только для одного узла, так как уравнение, составленное для второго узла, будет следствием первого уравнения.

При составлении уравнений по первому закону Кирхгофа необходимо соблюдать правило знаков: ток, подходящий к узлу, входит в уравнение со знаком «плюс»; ток, отходящий от узла, – со знаком «минус».

По первому закону Кирхгофа для узла В имеем

I₁ + I₂ + I₃ – I₄= 0. (1)

Недостающие три уравнения составляем по второму закону Кирхгофа для замкнутых контуров. Число независимых уравнений, которые могут быть составлены по закону Кирхгофа, также меньше числа контуров (в нашем случае контуров – шесть, а независимых уравнений – три). Чтобы составить необходимое число независимых уравнений, следует придерживаться правила: для составления уравнений выбирать контуры таким образом, чтобы в каждый новый контур входила хотя бы одна ветвь, не участвовавшая ни в одном из ранее использованных контуров.

При составлении уравнений по второму закону Кирхгофа необходимо соблюдать следующее правило знаков:

а) если ток по направлению совпадает с выбранным направлением обхода контуров, то соответствующее произведение IR входит в уравнение со знаком «плюс», в противном случае произведение IR входит в уравнение со знаком «минус»;

б) если ЭДС повышает потенциал в направлении обхода контура, т. е. если при обходе контура приходится идти от «минуса» к «плюсу» внутри источника, то соответствующая ЭДС входит в уравнение со знаком «плюс», в противном случае – со знаком «минус».

По второму закону Кирхгофа имеем:

для контура AR₁BR₂A

I₁R₁ – I₂R₂ = ε₁ – ε₂, (2)

для контура AR₁BR₃A

I₁R₁ – I₃R₃ = ε₁, (3)

для контура AR₃BR₄A

I₃R₃ + I₄R₄ = 0. (4)

Подставив в (1)–(4) числовые значения сопротивлений и ЭДС, получим систему уравнений

I₁ + I₂ + I₃ – I₄= 0,

2I₁ – 4I₂ = 6,

2I₁ – 4I₃ = 10,

4I₃ + 2I₄= 0.

Поскольку нужно найти только два тока, то удобно воспользоваться методом определителей (детерминантов). С этой целью перепишем уравнения еще раз в следующем виде:

I₁ + I₂ + I₃ – I₄= 0,

2I₁ – 4I₂ + 0 + 0 = 6,

2I₁ + 0 – 4I₃ + 0 = 10,

0 + 0 + 4I₃ + 2I₄= 0.

Искомые значения токов найдем из выражений

,

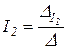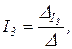
где Δ – определитель системы уравнени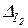й; и 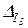– определители, полученные заменой соответствующих столбцов определителя Δ составленными из свободных членов четырех вышеприведенных уравнений.

Определитель системы

.

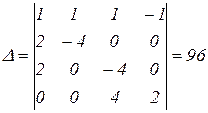Определители

.

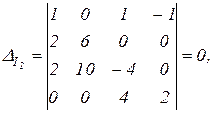
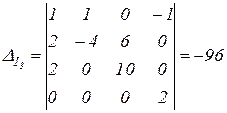Откуда получаем

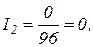
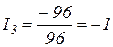А.

Знак «минус» у числового значения силы тока I₃ свидетельствует о том, что при произвольном выборе направлений токов, указанных на схеме, направление тока I₃ было указано противоположно истинному. На самом деле ток I₃ течет от узла В к узлу А.

Пример 6. ЭДС батареи равна 12 В. Наибольшая сила тока, которую может дать батарея, равна 5 А. Какая наибольшая мощность может выделиться на подключенном к батарее резисторе с переменным сопротивлением?

Решение. Мощность тока измеряется работой, совершенной электрическими силами в единицу времени. Поскольку вся работа на внешнем участке цепи идет на нагревание резистора, то в данном случае мощность измеряется количеством теплоты, выделяемым в резисторе в единицу времени. Поэтому на основании закона Джоуля – Ленца, а также закона Ома для замкнутой цепи получим

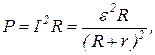(1)

где Р – мощность тока; I – сила тока; ε – ЭДС батареи; R, r – сопротивления внешнего и внутреннего участков цепи соответственно.

Отсюда видно, что при постоянных величинах ε, r мощность Р является функцией одной переменной – внешнего сопротивления R. Известно, что эта функция имеет максимум при условии (R = r), в этом можно убедиться, применив общий метод исследования функций на экстремум с помощью производной. Следовательно,

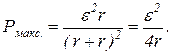(2)

Таким образом, задача сводится к отысканию сопротивления внутреннего участка цепи (батареи). Если учесть, что согласно закону Ома для замкнутой цепи наибольшая сила тока будет при внешнем сопротивлении R = 0 (ток короткого замыкания), то

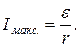(3)

Подставив найденное из (3) значение внутреннего сопротивления в формулу (2), получим

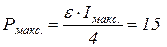Вт.

Пример 7. При какой постоянной силе тока через поперечное сечение проводника проходит заряд 50 Кл за промежуток времени от 5 до 10 с от момента включения тока? Какой заряд пройдет через поперечное сечение проводника за то же время, если сила тока в проводнике изменяется со временем по закону I = 6 + 3t?

Решение. Если сила тока постоянна, то I =Δq/Δt, где Δt = t₂ – t₁. Тогда

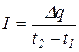=10 А.

Если сила тока изменяется со временем, то заряд, прошедший через поперечное сечение проводника за тот же промежуток времени,

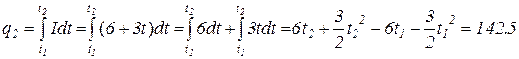Кл.

Пример 8. По медному проводнику с поперечным сечением 1 мм² течет ток силой 10 А. Определить среднюю скорость упорядоченного движения (скорость дрейфа) электронов в проводнике.

Решение. Плотность тока

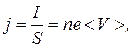
где I – сила тока; S – площадь поперечного сечения проводника; n – концентрация электронов проводимости; е – заряд электронов; < V > – скорость дрейфа электронов.

Поэтому скорость дрейфа равна

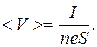
Каждый атом меди выделяет один электрон проводимости. Тогда концентрация электронов проводимости будет равна концентрации атомов меди в проводнике. Концентрация атомов меди

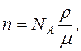
где N_A – число Авогадро; (ρ = 8,9 × 10³ кг/м³) – плотность меди;
(μ = 63,5 × 10^–3 кг/моль) – молярная масса. Тогда скорость дрейфа электронов

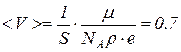мм/с.