Раздел 1.
Элементы линейной алгебры.
Линейные действия над матрицами и их свойства
Определение
Числовой матрицей (матрицей) размера  будем называть прямоугольную таблицу чисел, содержащую
будем называть прямоугольную таблицу чисел, содержащую  строк и
строк и  столбцов, и обозначать
столбцов, и обозначать  или
или 
 .
.
Матрица 
 , содержащая один столбец, называется столбцом.
, содержащая один столбец, называется столбцом.
Матрица 
 , содержащая одну строку, называется строкой.
, содержащая одну строку, называется строкой.
Столбцы и строки будем обозначать как векторы -  .
.
Пример. Матрица 
 содержит свои элементы в 3-х строках и 3-х столбцах.
содержит свои элементы в 3-х строках и 3-х столбцах.
Обозначение:  =
=  или
или  = |
= |  |,
|,  =1,2,3,
=1,2,3,  =1,2,3
=1,2,3
 - обозначение элемента матрицы, расположенного в
- обозначение элемента матрицы, расположенного в  -й строке, и
-й строке, и  -м столбце, (
-м столбце, ( =1,2,3,
=1,2,3,  =1,2,3);
=1,2,3);
 - индекс, указывающий номер строки;
- индекс, указывающий номер строки;
 - индекс, указывающий номер столбца.
- индекс, указывающий номер столбца.
Линейными действиями над матрицами называются операции сложения матриц, и умножения матрицы на число.
Определение
При сложение матриц 
 и
и 
 образуется матрица
образуется матрица 
 , каждый элемент которой равен сумме соответствующих элементов матриц
, каждый элемент которой равен сумме соответствующих элементов матриц 
 и
и 
 .
.
Обозначение суммы матриц:  =
=  +
+ 
где 
 =|
=|  |,
|, 
 =|
=|  |,
|, 
 =|
=|  |,
|,  =
=  +
+  ,
,  =1,…,n,
=1,…,n,  =1,…,m.
=1,…,m.
Пример №.  +
+  =
= 
Определение
|
|
|
При умножении матрицы 
 на
на  образуется матрица
образуется матрица 
 , каждый элемент которой равен произведению соответствующего элемента матрицы
, каждый элемент которой равен произведению соответствующего элемента матрицы  на
на  .
.
Обозначение произведения матрицы на число:  =
= 

где 
 =|
=|  |,
|, 
 =|
=|  |,
|,  =
= 
 ,
,  =1,…,n,
=1,…,n,  =1,…,m,
=1,…,m,  .
.
Пример. 3 
 =
= 
Определение
Линейной комбинацией столбцов  с коэффициентами
с коэффициентами  называется выражение вида:
называется выражение вида:
 =
= 
Пример. Столбец  =
=  является линейной комбинацией столбцов
является линейной комбинацией столбцов  =
=  и
и  =
=  с коэффициентами 1, 2.
с коэффициентами 1, 2.
 линейно выражается через
линейно выражается через  и
и  :
:  =
=  + 2
+ 2  ó
ó  =
=  =
=  +2
+2  .
.
Аналогично вводится понятие линейной комбинации матриц  с коэффициентами
с коэффициентами  :
:  =
=  .
.
Линейные свойства матриц:
Пусть

 =|
=|  |,
|, 
 =|
=|  |,
|,  =1,…,n,
=1,…,n,  =1,…,m,
=1,…,m,  ,
,  ,
,
тогда:
1. A + B = B + A (коммутативность)
2.(A + B) + C = A + (B + C) (ассоциативность)
3.  (A + B) =
(A + B) =  A +
A +  B (дистрибутивность)
B (дистрибутивность)
4.( +
+  ) A =
) A =  A +
A +  A (дистрибутивность)
A (дистрибутивность)
5.(
 ) A =
) A =  (
( A) (ассоциативность)
A) (ассоциативность)
2. Произведение матриц и их свойства
Определение.
Произведением матриц 
 и
и 
 называется матрица
называется матрица 
 ,
,
элементы которой определяются по формуле:
 =
=  , (
, ( =1,…,n,
=1,…,n,  =1,…,k).
=1,…,k).
Обозначение:  =
=  ,
, 
 =|
=|  |.
|.
Пример. Пусть 
 ,
, 
 . Найти
. Найти  =
=  .
.
 =
=  =
= 
 +
+ 
 +…+
+…+ 
 ,
,
 =
=  =
= 
 +
+ 
 +…+
+…+ 
 ,
,
 =
=  =
= 
 +
+ 
 +…+
+…+ 
 , и т.д.
, и т.д.
Матрицы  и
и  можно перемножить, если число столбцов матрицы
можно перемножить, если число столбцов матрицы  (т.е. длина строки матрицы
(т.е. длина строки матрицы  ) равно числу строк матрицы
) равно числу строк матрицы  (т.е. длине столбца матрицы
(т.е. длине столбца матрицы  ).
).
Количество строк матрицы  (где
(где  =
=  ) определяется количеством строк матрицы
) определяется количеством строк матрицы  , а количество столбцов – количеством столбцов матрицы B.
, а количество столбцов – количеством столбцов матрицы B.
Пример. 

 =
=  =
= 
 = 3
= 3  1 + 1
1 + 1  0 + 0
0 + 0  1 + 2
1 + 2  3 = 9
3 = 9  = 6
= 6  1 + 2
1 + 2  0 + 0
0 + 0  1 + 4
1 + 4  3 = 18
3 = 18
 = 3
= 3  2 + 1
2 + 1  3 + 0
3 + 0  7 + 2
7 + 2  0 = 9
0 = 9  = 6
= 6  2 + 2
2 + 2  3 + 0
3 + 0  7 + 4
7 + 4  0 = 18
0 = 18
 = 3
= 3  7 + 1
7 + 1  0 + 0
0 + 0  9 - 2
9 - 2  6 = 9
6 = 9  = 6
= 6  7 + 2
7 + 2  0 + 0
0 + 0  9 - 4
9 - 4  6 = 18
6 = 18
Свойства произведения матриц:
1.  =
=  (ассоциативность)
(ассоциативность)
2.  =
=  +
+  (дистрибутивность)
(дистрибутивность)
В общем случае произведение матриц не коммутативно, т.е. 
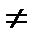
 .
.
Если  =
=  , тогда матрицы
, тогда матрицы  и
и  называются перестановочными.
называются перестановочными.
|
|
|
Пример. Умножим матрицу  =
=  на столбец
на столбец  =
= 
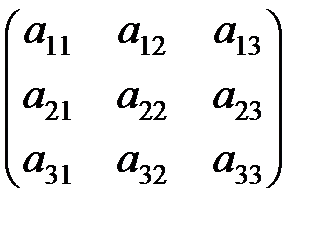
 =
= 


 =
=  ó
ó 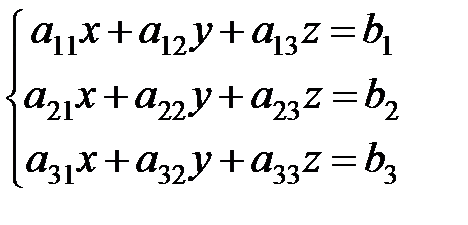
Матричной записью системы линейных уравнений
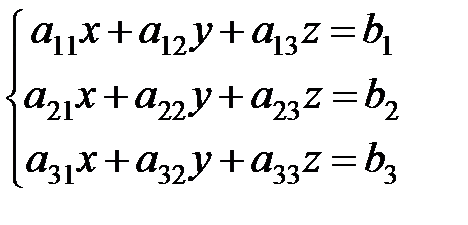
называется выражение вида: 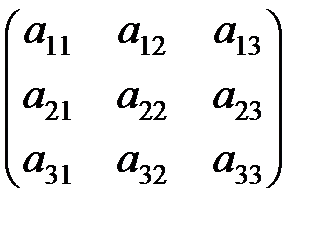
 =
=  , или кратко:
, или кратко:  =
=  ,
,
где:
 =
= 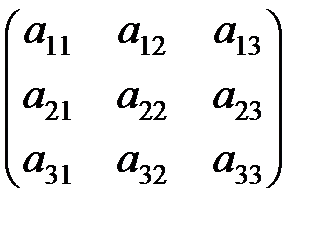 - матрица системы;
- матрица системы;
 =
=  - столбец неизвестных;
- столбец неизвестных;  =
=  - столбец свободных членов.
- столбец свободных членов.
Определители 2-го и 3-го порядка и их свойства
Определение
Выражение вида  , где
, где 
 ,
,  =1,2,
=1,2,  =1,2,
=1,2,
которое вычисляется по формуле  ,
,
называется определителем второго порядка матрицы  =
=  .
.
Пример. Вычислить определитель:  .
.
Определение
Выражение вида
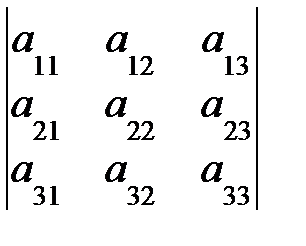 , где
, где 
 ,
,  =1,2,3,
=1,2,3,  =1,2,3,
=1,2,3,
которое вычисляется по формуле
 =
= 

 +
+ 

 +
+ 

 -
- 

 -
- 

 -
- 

 ,
,
называется определителем третьего порядка матрицы  =
= 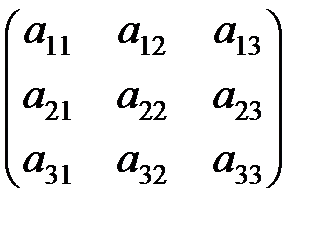 .
.
В алгебраическую сумму, определяющую определитель третьего порядка, со знаком плюс входят произведения следующих элементов:
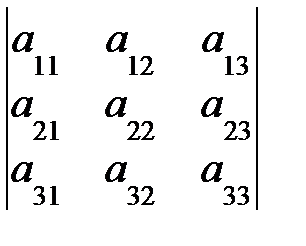
со знаком минус:
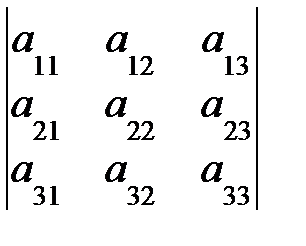 .
.
det  - обозначение определителя (детерминанта) матрицы
- обозначение определителя (детерминанта) матрицы  .
.
Свойства определителей разберем на примере определителей 2-го и 3-го порядка.
1. Определитель матрицы не изменяется при ее транспонировании
det  = det
= det  , где
, где  =
=  ,
,  =
= 
 - обозначение транспонированной матрицы
- обозначение транспонированной матрицы  .
.
Транспонирование – это процедура, связанная с заменой строк матрицы на столбцы
 =
=  =
= 
Из первого свойства следует, что любое свойство, сформулированное для строк определителя, справедливо и для столбцов, и - наоборот.
2. Знак определителя изменится на противоположный, если поменять местами два столбца (строки)
 =
=  =
=  =
= 
3. Определитель равен нулю, если содержит нулевой столбец (строку)
 = 0
= 0
4. Определитель равен нулю, если содержит два одинаковые столбца (строки)
 =
=  = 0
= 0
5. Коэффициент, на который умножены все элементы некоторого столбца (строки) можно выносить за определитель, как множитель.
 =
= 

 =
=  =
=  =
= 

 =
= 

Пример.  =
= 
6. Определитель равен нулю, если содержит пропорциональные столбцы (строки)
 = 0 ó
= 0 ó  =
= 
 = 0 (см. свойство 4)
= 0 (см. свойство 4)
7. Если в определителе каждый элемент некоторого i-го столбца представлен суммой двух слагаемых, тогда данный определитель может быть представлен суммой двух определителей того же порядка.
Столбцы полученных определителей, кроме i-го столбца, совпадают со столбцами исходного определителя.
i-й столбец первого полученного определителя состоит соответственно из первых слагаемых в суммах, которыми представлены соответствующие элементы i-го столбца исходного определителя.
i-й столбец второго полученного определителя состоит соответственно из вторых слагаемых в суммах, которыми представлены соответствующие элементы i-го столбца исходного определителя.
 =
=  +
+ 
В силу свойства 1, данное свойство справедливо и для строк.
Утверждение
Определитель не изменится, если к одному из его столбцов прибавить другой его столбец, умноженный на константу (см.свойства 7,6).
В силу свойства 1, данное утверждение справедливо и для строк.
8. Определитель равен нулю, если один из его столбцов (строк) представляет собой линейную комбинацию некоторых других столбцов (строк).
Рассмотрим определитель
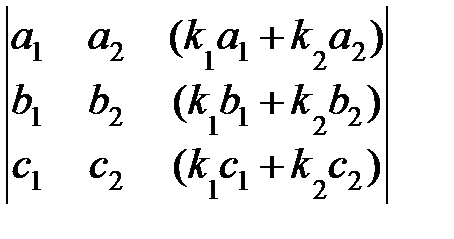 ;
;
у которого третий столбец представляет собой линейную комбинацию первого и второго столбцов с коэффициентами 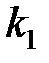 и
и  :
:
 =
= 
 +
+ 

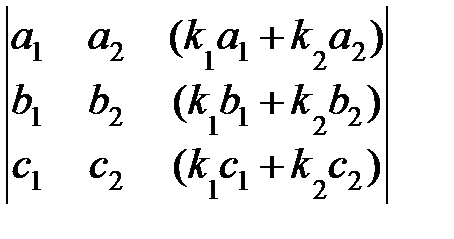 = 0 ó
= 0 ó
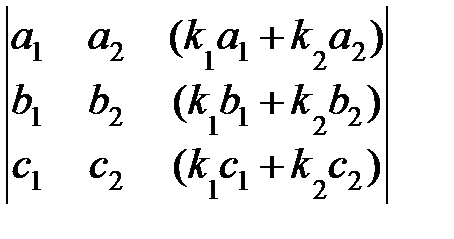 =
=  +
+  = 0 + 0
= 0 + 0
(см.свойства 7,6)
 2015-10-22
2015-10-22 6450
6450