Математическая модель задачи линейного программирования

Т10. Постановка задачи линейного программирования

Математической моделью экономической задачи называется совокупность математических соотношений, описывающих экономический процесс.

Для составления математической модели необходимо:

1. выбрать переменные задачи;

2. составить систему ограничений;

3. задать целевую функцию.

Переменными задачи называются величины х₁, х₂,…, х_n, которые полностью характеризуют экономический процесс. Их обычно записывают в виде вектора Х = (х₁, х₂,…, х_n).

Системой ограничений задачи называется совокупность уравнений и неравенств, которым удовлетворяют переменные задачи и которые следуют из ограниченности ресурсов и других экономических условий, например, положительности переменных. В общем случае они имеют вид:

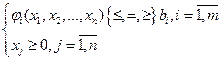. (1)

Целевой функцией называется функция F(X) = f(х₁, х₂,…, х_n) переменных задачи, которая характеризует качество выполнения задачи и экстремум которой требуется найти.

Общая задача математического программирования формулируется следующим образом: найти переменные задачи х₁, х₂,…, х_n, которые обеспечивают экстремум целевой функции

F(X) = f(х₁, х₂,…, х_n) ® max (min) (2)

и удовлетворяют системе ограничений (1).

Если целевая функция (2) и система ограничений (1) линейны, то задача математического программирования называется задачей линейного программирования (ЗЛП).

Вектор Х (набор переменных задачи) называется допустимым решением, или планом ЗЛП, если он удовлетворяет системе ограничений (1). Допустимый план Х, который обеспечивает экстремум целевой функции, называется оптимальным решением ЗЛП.

 

2. Примеры составления математических моделей экономических задач

 

К ЗЛП приводит исследование конкретных производственных ситуаций, которые интерпретируются как задачи об оптимальном использовании ограниченных ресурсов.

1. Задача об оптимальном производственном плане

 

Для производства двух типов изделий Т₁ и Т₂ используются три вида ресурсов S₁, S₂, S₃. Запасы ресурсов, число единиц ресурсов, затрачиваемых на изготовление единицы продукции, а также прибыль от реализации единицы продукции приведены в таблице:

 

Вид ресурса	Запас ресурса	Число единиц ресурсов, затрачиваемых на изготовление единицы продукции
Т1	Т2
S1 S2 S3			-
Прибыль, ден.ед.

 

Требуется найти такой план производства продукции, при котором прибыль от ее реализации будет максимальной.

 

Решение.

Обозначим х₁, х₂ – число единиц продукции соответственно Т₁ и Т₂, запланированных к производству. Для их изготовления потребуется (х₁ + х₂) единиц ресурса S₁, (х₁ + 4х₂) единиц ресурса S₂, (х₁) единиц ресурса S₃. Потребление ресурсов S₁, S₂, S₃ не должно превышать их запасов, соответственно 8, 20 и 5 единиц.

Тогда экономико-математическую модель задачи можно сформулировать так:

 

Найти план выпуска продукции Х = (х₁, х₂), удовлетворяющий системе ограничений: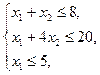

и условию ,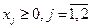

при котором функция 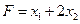принимает максимальное значение.

Задачу можно легко обобщить на случай выпуска n типов продукции с использованием m видов ресурсов.

 

 

2. Задача об оптимальном рационе

 

Имеется два вида корма К₁ и К₂, содержащие питательные вещества S₁, S₂ и S₃. Содержание числа единиц питательных веществ в 1кг каждого вида корма, необходимый минимум питательных веществ, а также стоимость 1кг корма приведены в таблице:

 

Питательное вещество	Необходимый минимум питательных веществ	Число единиц питательных веществ в 1кг корма
К1	К2
S1 S2 S3
Cтоимость 1кг корма, ден.ед.

 

Необходимо составить дневной рацион, имеющий минимальную стоимость, в котором содержание каждого вида питательных веществ было бы не менее установленного предела.

Решение.

Обозначим х₁, х₂ – количество кормов К₁ и К₂, входящих в дневной рацион. Тогда этот рацион будет включать (3х₁ + х₂) единиц питательного вещества S₁, (х₁ +2х₂) единиц вещества S₂, (х₁+6х₂) единиц питательно вещества S₃. Так как содержание питательных веществ S₁, S₂ и S₃ в рационе должно быть соответственно 9, 8 и 12 единиц, то экономико-математическую модель задачи можно сформулировать так:

Составить дневной рацион Х = (х₁, х₂), удовлетворяющий системе ограничений: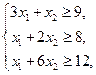

и условию ,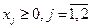

при котором функция 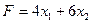принимает минимальное значение.

 

Формы записи ЗЛП

 

В ЗЛП требуется найти экстремум линейной целевой функции:

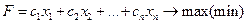
при ограничениях:

и условии неотрицательности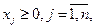

где а_ij, b_i, c_j (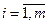, ) – заданные постоянные величины.

Так записывается ЗЛП в общей форме. Если система ограничений содержит только неравенства, то ЗЛП представлена в стандартной форме. Канонической (основной) формой записи ЗЛП называется запись, когда система ограничений содержит только равенства. Так что приведенные выше ЗЛП записаны в стандартной форме.

Общая, стандартная и каноническая формы ЗЛП эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть переписана в другой форме. Это значит, что если есть способ решения одной из указанных задач, то может быть определен оптимальный план любой из задач.

Чтобы перейти от одной формы записи ЗЛП к другой надо уметь переходить от ограничений-неравенств к ограничениям-равенствам и наоборот.

Ограничение – неравенство (£) можно преобразовать к ограничению-равенству добавлением к его левой части дополнительной неотрицательной переменной, а ограничение-неравенство (³) – в ограничение равенство вычитанием из его левой части дополнительной неотрицательной переменной. Число вводимых дополнительных неотрицательных переменных равно числу преобразуемых ограничений-неравенств.

Вводимые дополнительные переменные имеют определенный экономический смысл. Так, если в ограничениях исходной ЗЛП отражаются расход и наличие ресурсов, то значение дополнительной переменной ЗЛП в канонической форме равно объему неиспользуемого соответствующего ресурса.

Пример 1. Записать в канонической форме ЗЛП:

Найти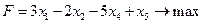

при ограничениях:

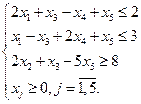
Решение.

Целевая функция остается без изменений:

.

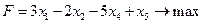Система неравенств преобразуется в систему равенств:

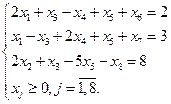
При решении ЗЛП графическим методом требуется переход от канонической формы к стандартной форме.

Для приведения ЗЛП к стандартной форме используется метод Жордана – Гаусса решения СЛАУ. В отличие от метода Гаусса, в котором расширенная матрица системы приводится к ступенчатому виду, в методе Жордана – Гаусса в составе расширенной матрицы формируется единичная матрица. Поэтому обратный ход здесь не требуется.

Для преобразования исходной канонической ЗЛП в эквивалентную стандартную ЗЛП:

а) в расширенной матрице системы ограничений выбирается отличный от нуля элемент a_qp. Этот элемент называется разрешающим, а q - я строка и р-й столбец называются разрешающей строкой и разрешающим столбцом.

б) разрешающая строка переписывается без изменения, а все элементы разрешающего столбца, кроме разрешающего, заменяются нулями. Остальные элементы расширенной матрицы определяются с помощью «правила прямоугольника»:

Рассмотрим четыре элемента расширенной матрицы: элемент а_ij, подлежащий преобразованию, разрешающий элемент a_qp и элементы а_iр и a_qj. Для нахождения элемента а_ij следует из элемента а_ij вычесть произведение элементов а_iр и a_qj, расположенных в противоположных вершинах прямоугольника, деленное на разрешающий элемент a_qp:

в) одновременно исключаются разрешенные неизвестные из целевой функции. Для этого в расширенной матрице в последней строке записываются коэффициенты целевой функции. При вычислениях учитывается, что разрешающий элемент в последней строке выбирать нельзя.

 

Пример 2. Привести к стандартному виду:

,

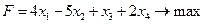Решение.

Методом Жордана – Гаусса приведем систему уравнений-ограничений ЗЛП к равносильной системе неравенств. Выберем в качестве разрешающего элемента третий элемент первой строки:

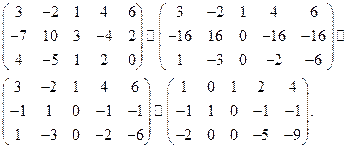
Число -9, полученное в последнем столбце последней строки, необходимо записать в целевую функцию с противоположным знаком. В результате преобразований ЗЛП принимает вид:

,

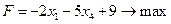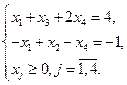
Т.к. переменные х₂ и х₃ неотрицательные, то отбросив их, можно записать ЗЛП в симметричном виде:

,

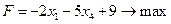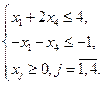
В канонической форме ЗЛП целевая функция может как минимизироваться, так и максимизироваться. Чтобы перейти от нахождения максимума к нахождению минимума или наоборот, достаточно изменить знаки коэффициентов целевой функции: F₁ = - F. Полученная в результате этого задача и исходная ЗЛП имеют одно и то же оптимальное решение, а значения целевых функций на этом решении отличаются только знаком.

 

Свойства ЗЛП

 

1. Множество всех допустимых решений системы ограничений задачи линейного программирования является выпуклым.

Множество точек называется выпуклым, если оно содержит весь отрезок, соединяющий две любые точки этого множества.

Согласно этому определению многоугольник на рис.1а является выпуклым множеством, а многоугольник на рис.1б таковым не является, т.к. отрезок MN между двумя его точками M и N не полностью принадлежит этому многоугольнику.

Рис.1

Выпуклыми множествами могут быть не только многоугольники. Примерами выпуклых множеств являются круг, сектор, отрезок, куб, пирамида и т.п.

 

2. Если ЗЛП имеет оптимальное решение, то линейная функция принимает максимальное (минимальное) значение в одной из угловых точек многогранника решений. Если линейная функция принимает максимальное (минимальное) значение более чем в одной угловой точке, то она принимает его в любой точке, являющейся выпуклой линейной комбинацией этих точек.

Точка Х называется выпуклой линейной комбинацией точек Х₁, Х₂,…, Х_n, если выполняются условия:

Х = α₁Х₁+α₂Х₂+…+ α_nХ_n,

α_j ≥ 0, Σα_j = 1.

Очевидно, что в частном случае при n = 2 выпуклой линейной комбинацией двух точек является соединяющий их отрезок.

 

3. Каждому допустимому базисному решению системы ограничений канонической ЗЛП соответствует угловая точка многогранника решений, и наоборот, каждой угловой точке многогранника решений соответствует допустимое базисное решение.

 

Из двух последних свойств следует: если ЗЛП имеет оптимальное решение, то оно совпадает, по крайней мере, с одним из ее допустимых базисных решений.

Таким образом, экстремум линейной функции ЗЛП надо искать среди конечного числа ее допустимых базисных решений.