2015-05-13
5539ВВЕДЕНИЕ.. 5
1. ВВЕДЕНИЕ В ТЕОРИЮ АЛГОРИТМОВ.. 6
1.1 Исторический обзор. 6
1.2 Цели и задачи теории алгоритмов. 7
1.3 Практическое применение результатов теории алгоритмов. 8
1.4 Формализация понятия алгоритма.. 8
1.5 Вопросы для самоконтроля. 10
2. МАШИНА ПОСТА.. 11
2.1 Основные понятия и операции.. 11
2.2 Финитный 1 – процесс. 12
2.3 Способ задания проблемы и формулировка 1. 13
2.4 Вопросы для самоконтроля. 14
3. МАШИНА ТЬЮРИНГА И АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ... 15
3.1. Машина Тьюринга.. 15
3.2. Алгоритмически неразрешимые проблемы.. 17
3.3. Проблема соответствий Поста над алфавитом Σ.. 20
3.4 Вопросы для самоконтроля. 22
4. ВВЕДЕНИЕ В АНАЛИЗ АЛГОРИТМОВ.. 23
4.1. Сравнительные оценки алгоритмов. 23
4.2 Система обозначений в анализе алгоритмов. 24
4.3 Классификация алгоритмов по виду функции трудоёмкости.. 25
4.4 Асимптотический анализ функций.. 27
4.5 Вопросы для самоконтроля. 30
5. ТРУДОЕМКОСТЬ АЛГОРИТМОВ И ВРЕМЕННЫЕ ОЦЕНКИ.. 31
5.1. Элементарные операции в языке записи алгоритмов. 31
5.2 Примеры анализа простых алгоритмов. 32
5.3. Переход к временным оценкам.. 34
5.4 Пример пооперационного временного анализа.. 36
5.5 Вопросы для самоконтроля. 38
6. ТЕОРИЯ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ И СЛОЖНОСТНЫЕ КЛАССЫ ЗАДАЧ.. 39
6.1 Теоретический предел трудоемкости задачи.. 39
6.2 Сложностные классы задач. 40
6.3 Проблема P = NP.. 41
6.4 Класс NPC (NP – полные задачи) 42
6.5 Примеры NP – полных задач. 44
6.6 Вопросы для самоконтроля. 45
7. ПРИМЕР ПОЛНОГО АНАЛИЗА АЛГОРИТМА РЕШЕНИЯ ЗАДАЧИ О СУММЕ.. 47
7.1 Формулировка задачи и асимптотическая оценка.. 47
7.2 Алгоритм точного решения задачи о сумме (метод перебора) 48
7.3 Анализ алгоритма точного решения задачи о сумме. 49
7.4 Вопросы для самоконтроля. 51
8. РЕКУРСИВНЫЕ ФУНКЦИИ И АЛГОРИТМЫ... 52
8.1 Рекурсивные функции.. 52
8.2 Рекурсивная реализация алгоритмов. 54
8.3 Анализ трудоемкости механизма вызова процедуры.. 56
8.4 Анализ трудоемкости алгоритма вычисления факториала.. 57
8.5 Вопросы для самоконтроля. 58
9. РЕКУРСИВНЫЕ АЛГОРИТМЫ И МЕТОДЫ ИХ АНАЛИЗА.. 59
9.1 Логарифмические тождества.. 59
9.2 Методы решения рекурсивных соотношений.. 59
9.3 Рекурсивные алгоритмы. 60
9.4 Основная теорема о рекуррентных соотношениях.. 61
9.5 Вопросы для самоконтроля. 61
10. ПРЯМОЙ АНАЛИЗ РЕКУРСИВНОГО ДЕРЕВА ВЫЗОВОВ.. 62
10.1 Алгоритм сортировки слиянием.. 62
10.2 Слияние отсортированных частей (Merge) 62
10.3 Подсчет вершин в дереве рекурсивных вызовов. 64
10.4 Анализ трудоемкости алгоритма сортировка слиянием.. 64
10.5 Вопросы для самоконтроля. 65
11. ТЕОРИЯ И АЛГОРИТМЫ МОДУЛЯРНОЙ АРИФМЕТИКИ.. 67
11.1 Алгоритм возведения числа в целую степень. 67
11.2 Сведения из теории групп.. 69
11.3 Сведения из теории простых чисел. 70
11.4 Вопросы для самоконтроля. 71
12. КРИПТОСИСТЕМА RSA И ТЕОРИЯ АЛГОРИТМОВ.. 72
12.1 Мультипликативная группа вычетов по модулю n. 72
12.2 Степени элементов в Zn* и поиск больших простых чисел. 73
12.3 Криптосистема RSA.. 74
12.4 Криптостойкость RSA и сложность алгоритмов факторизации.. 74
12.5 Вопросы для самоконтроля. 75
ЭКЗАМЕНАЦИОННЫЕ ВОПРОСЫ... 76
ЛИТЕРАТУРА.. 79
ВВЕДЕНИЕ
Теория алгоритмов - это наука, изучающая общие свойства и закономерности алгоритмов, разнообразные формальные модели их представления. На основе формализации понятия алгоритма возможно сравнение алгоритмов по их эффективности, проверка их эквивалентности, определение областей применимости.
Разработанные в 1930-х годах разнообразные формальные модели алгоритмов (Пост, Тьюринг, Черч), равно как и предложенные в 1950-х годах модели Колмогорова и Маркова, оказались эквивалентными в том смысле, что любой класс проблем, разрешимых в одной модели, разрешимы и в другой.
В настоящее время полученные на основе теории алгоритмов практические рекомендации получают всё большее распространение в области проектирования и разработки программных систем. В связи с этим в государственный стандарт введёна специальная дисциплина “Математическая логика и теория алгоритмов”. Описание государственного стандарта регламентирует включение в состав дисциплины ряда понятий и методов теории алгоритмов, которые и отражены в настоящем учебном пособии.
Во второй части учебного пособия рассмотрены основы таких разделов теории алгоритмов как: классическая теория алгоритмов (машина Поста, машина Тьюринга, алгоритмически неразрешимые проблемы), асимптотический анализ сложности алгоритмов, включая сложность рекурсивных реализаций, сложностные классы P, NP, NPC, включая проблему P = NP и практический сравнительный анализ алгоритмов. На примере криптосистемы RSA показана практическая важность результатов теории алгоритмов.
1. ВВЕДЕНИЕ В ТЕОРИЮ АЛГОРИТМОВ
1.1 Исторический обзор
Первым дошедшим до нас алгоритмом в его интуитивном понимании – конечной последовательности элементарных действий, решающих поставленную задачу, считается предложенный Евклидом в III веке до нашей эры алгоритм нахождения наибольшего общего делителя двух чисел (алгоритм Евклида). Отметим, что в течение длительного времени, вплоть до начала XX века само слово «алгоритм» употреблялось в устойчивом сочетании «алгоритм Евклида». Для описания пошагового решения других математических задач использовалось слово «метод».
Начальной точкой отсчета современной теории алгоритмов можно считать работу немецкого математика Курта Гёделя [4] (1931 год - теорема о неполноте символических логик), в которой было показано, что некоторые математические проблемы не могут быть решены алгоритмами из некоторого класса. Общность результата Геделя связана с тем, совпадает ли использованный им класс алгоритмов с классом всех (в интуитивном смысле) алгоритмов. Эта работа дала толчок к поиску и анализу различных формализаций алгоритма.
Первые фундаментальные работы по теории алгоритмов были опубликованы независимо в 1936 году годы Аланом Тьюрингом, Алоизом Черчем и Эмилем Постом. Предложенные ими машина Тьюринга, машина Поста и лямбда-исчисление Черча были эквивалентными формализмами алгоритма. Сформулированные ими тезисы (Поста и Черча-Тьюринга) постулировали эквивалентность предложенных ими формальных систем и интуитивного понятия алгоритма. Важным развитием этих работ стала формулировка и доказательство алгоритмически неразрешимых проблем.
В 1950-е годы существенный вклад в теорию алгоритмов внесли работы Колмогорова и Маркова.
К 1960-70-ым годам оформились следующие направления в теории алгоритмов:
· Классическая теория алгоритмов (формулировка задач в терминах формальных языков, понятие задачи разрешения, введение сложностных классов, формулировка в 1965 году Эдмондсом проблемы P=NP, открытие класса NP -полных задач и его исследование) [6];
· Теория асимптотического анализа алгоритмов (понятие сложности и трудоёмкости алгоритма, критерии оценки алгоритмов, методы получения асимптотических оценок, в частности для рекурсивных алгоритмов, асимптотический анализ трудоемкости или времени выполнения), в развитие которой внесли существенный вклад Кнут, Ахо, Хопкрофт, Ульман, Карп [1, 2, 5];
· Теория практического анализа вычислительных алгоритмов (получение явных функции трудоёмкости, интервальный анализ функций, практические критерии качества алгоритмов, методика выбора рациональных алгоритмов), основополагающей работой в этом направлении, очевидно, следует считать фундаментальный труд Д. Кнута «Искусство программирования для ЭВМ» [5].
1.2 Цели и задачи теории алгоритмов
Обобщая результаты различных разделов теории алгоритмов можно выделить следующие цели и соотнесенные с ними задачи, решаемые в теории алгоритмов:
· формализация понятия «алгоритм» и исследование формальных алгоритмических систем;
· формальное доказательство алгоритмической неразрешимости ряда задач;
· классификация задач, определение и исследование сложностных классов;
· асимптотический анализ сложности алгоритмов;
· исследование и анализ рекурсивных алгоритмов;
· получение явных функций трудоемкости в целях сравнительного анализа алгоритмов;
· разработка критериев сравнительной оценки качества алгоритмов.
1.3 Практическое применение результатов теории алгоритмов
Полученные в теории алгоритмов теоретические результаты находят достаточно широкое практическое применение, при этом можно выделить следующие два аспекта:
Теоретический аспект: при исследовании некоторой задачи результаты теории алгоритмов позволяют ответить на вопрос – является ли эта задача в принципе алгоритмически разрешимой – для алгоритмически неразрешимых задач возможно их сведение к задаче останова машины Тьюринга. В случае алгоритмической разрешимости задачи – следующий важный теоретический вопрос – это вопрос о принадлежности этой задачи к классу NP –полных задач, при утвердительном ответе на который, можно говорить о существенных временных затратах для получения точного решения для больших размерностей исходных данных.
Практический аспект: методы и методики теории алгоритмов (в основном разделов асимптотического и практического анализа) позволяют осуществить:
· рациональный выбор из известного множества алгоритмов решения данной задачи с учетом особенностей их применения (например, при ограничениях на размерность исходных данных или объема дополнительной памяти);
· получение временных оценок решения сложных задач;
· получение достоверных оценок невозможности решения некоторой задачи за определенное время, что важно для криптографических методов;
· разработку и совершенствование эффективных алгоритмов решения задач в области обработки информации на основе практического анализа.
1.4 Формализация понятия алгоритма
Во всех сферах своей деятельности, и частности в сфере обработки информации, человек сталкивается с различными способами или методиками решения задач. Они определяют порядок выполнения действий для получения желаемого результата – мы можем трактовать это как первоначальное или интуитивное определение алгоритма. Некоторые дополнительные требования приводят к неформальному определению алгоритма:
Определение 1.1: Алгоритм - это заданное на некотором языке конечное предписание, задающее конечную последовательность выполнимых элементарных операций для решения задачи, общее для класса возможных исходных данных.
Пусть D – область (множество) исходных данных задачи, а R – множество возможных результатов, тогда мы можем говорить, что алгоритм осуществляет отображение D → R. Поскольку такое отображение может быть не полным, то вводятся следующие понятия:
Алгоритм называется частичным алгоритмом, если мы получаем результат только для некоторых d є D и полным алгоритмом, если алгоритм получает правильный результат для всех d є D.
Несмотря на усилия исследователей отсутствует одно исчерпывающе строгое определение понятия алгоритм, в теории алгоритмов были введены различные формальные определения алгоритма и удивительным научным результатом является доказательство эквивалентности этих формальных определений в смысле их равномощности.
Варианты словесного определения алгоритма принадлежат российским ученым А.Н. Колмогорову и А.А. Маркову [10]:
Определение 1.2 (Колмогоров): Алгоритм – это всякая система вычислений, выполняемых по строго определенным правилам, которая после какого-либо числа шагов заведомо приводит к решению поставленной задачи.
Определение 1.3 (Марков): Алгоритм – это точное предписание, определяющее вычислительный процесс, идущий от варьируемых исходных данных к искомому результату.
Отметим, что различные определения алгоритма, в явной или неявной форме, постулируют следующий ряд требований:
· алгоритм должен содержать конечное количество элементарно выполнимых предписаний, т.е. удовлетворять требованию конечности записи;
· алгоритм должен выполнять конечное количество шагов при решении задачи, т.е. удовлетворять требованию конечности действий;
· алгоритм должен быть единым для всех допустимых исходных данных, т.е. удовлетворять требованию универсальности;
· алгоритм должен приводить к правильному по отношению к поставленной задаче решению, т.е. удовлетворять требованию правильности.
Другие формальные определения понятия алгоритма связаны с введением специальных математических конструкций (машина Поста, машина Тьюринга, рекурсивно-вычислимые функции Черча) и постулированием тезиса об эквивалентности такого формализма и понятия «алгоритм».
Рассмотрению машины Поста и машины Тьюринга посвящены следующие два раздела учебного пособия.
1.5 Вопросы для самоконтроля
1) Исторические аспекты создания и разработки теории алгоритмов;
2) Цели и задачи классической теории алгоритмов;
3) Цели и задачи теории асимптотического анализа алгоритмов;
4) Цели и задачи практического анализа алгоритмов;
5) Теоретический и практический аспекты применения результатов теории алгоритмов;
6) Формализация алгоритма, определения Колмогорова и Маркова;
7) Требования к алгоритму, связанные с формальными определениями;
2. МАШИНА ПОСТА
2.1 Основные понятия и операции
Одной из фундаментальных статей, результаты которой лежат в основе современной теории алгоритмов является статья Эмиля Поста (Emil Post), «Финитные комбинаторные процессы, формулировка 1», опубликованная в 1936 году в сентябрьском номере «Журнала символической логики» [10].
Пост рассматривает общую проблему, состоящую из множества конкретных проблем, при этом решение общей проблемы это такое решение, которое доставляет ответ для каждой конкретной проблемы.
Например, решение уравнения 3*х+9=0 – это одна из конкретных проблем, а решение уравнения a*x+b=0 – это общая проблема, тем самым алгоритм (сам термин «алгоритм» не используется Постом) должен быть универсальным, т.е. должен быть соотнесен с общей проблемой.
Основные понятия алгоритмического формализма Поста – это пространство символов (язык L) в котором задаётся конкретная проблема и получается ответ, и набор инструкций, т.е. операций в пространстве символов, задающих как сами операции, так и порядок выполнения инструкций.
 |
Постовское пространство символов – это бесконечная лента ячеек (ящиков):
Каждый ящик или ячейка могут быть помечены или не помечены.
Конкретная проблема задается «внешней силой» (термин Поста) пометкой конечного количества ячеек, при этом, очевидно, что любая конфигурация начинается и заканчивается помеченным ящиком. После применения к конкретной проблеме некоторого набора инструкций решение представляется так же в виде набора помеченных и непомеченных ящиков, распознаваемое той же внешней силой.
Пост предложил набор инструкций (элементарных операций), которые выполняет «работник», отметим, что в 1936 году не было еще ни одной электронной вычислительной машины. Этот набор инструкций является, очевидно, минимальным набором битовых операций:
1. пометить ящик, если он пуст;
2. стереть метку, если она есть;
3. переместиться влево на 1 ящик;
4. переместиться вправо на 1 ящик;
5. определить помечен ящик или нет, и по результату перейти на одну из двух указанных инструкций;
6. остановиться.
Отметим, что формулировка инструкций 1 и 2 включает защиту от неправильных ситуаций.
Программа представляет собой нумерованную последовательность инструкций, причем переходы в инструкции 5 производятся на указанные в ней номера других инструкций.
2.2 Финитный 1 – процесс
Программа (набор инструкций в терминах Поста) является одной и той же для всех конкретных проблем, поэтому соотнесена с общей проблемой – таким образом, Пост формулирует требование универсальности.
Далее Пост вводит следующие понятия:
· набор инструкций применим к общей проблеме, если для каждой конкретной проблемы не возникает коллизий в инструкциях 1 и 2, т.е. никогда программа не стирает метку в пустом ящике и не устанавливает метку в помеченном ящике;
· набор инструкций заканчивается (за конечное количество инструкций), если выполняется инструкция (6);
· набор инструкций задаёт финитный 1 – процесс, если набор применим, и заканчивается для каждой конкретной проблемы;
· финитный 1 – процесс для общей проблемы есть 1 – решение, если ответ для каждой конкретной проблемы правильный (это определяется внешней силой).
2.3 Способ задания проблемы и формулировка 1
По Посту проблема задаётся внешней силой путем пометки конечного количества ящиков ленты. В более поздних работах по машине Поста [10] принято считать, что машина работает в единичной системе счисления (0=V; 1=VV; 2=VVV; 3=VVVV), т.е. ноль представляется одним помеченным ящиком, а целое положительное число – помеченными ящиками в количестве на единицу больше его значения.
Поскольку множество конкретных проблем, составляющих общую проблему счетное, то можно установить взаимно однозначное соответствие (биективное отображение) между множеством положительных целых чисел N и множеством конкретных проблем.
Общая проблема называется по Посту 1-заданой, если существует такой финитный 1 – процесс, что, будучи, применим к n є N в качестве исходной конфигурации ящиков, он задает n-ую конкретную проблему в виде набора помеченных ящиков.
Если общая проблема 1-задана и 1-разрешима, то, соединяя наборы инструкций по заданию проблемы, и ее решению мы получаем ответ по номеру проблемы – это и есть в терминах статьи Поста формулировка1.
Эмиль Пост завершает свою статью следующей фразой [10]: «Автор ожидает, что его формулировка окажется логически эквивалентной рекурсивности в смысле Геделя — Черча. Цель формулировки, однако, в том, чтобы предложить систему не только определенной логической силы, но и психологической достоверности. В этом последнем смысле подлежат рассмотрению всё более и более широкие формулировки. С другой стороны, нашей целью будет показать, что все они логически сводимы к формулировке 1. В настоящий момент мы выдвигаем это умозаключение в качестве рабочей гипотезы. … Успех вышеизложенной программы заключался бы для нас в превращении этой гипотезы не столько в определение или аксиому, сколько в закон природы».
 |
Таким образом, гипотеза Поста состоит в том, что любые более широкие формулировки в смысле алфавита символов ленты, набора инструкций, представления и интерпретации конкретных проблем сводимы к формулировке 1.
Следовательно, если гипотеза верна, то любые другие формальные определения, задающие некоторый класс алгоритмов, эквивалентны классу алгоритмов, заданных формулировкой 1 Эмиля Поста.
Обоснование этой гипотезы происходит сегодня не путем строго математического доказательства, а на пути эксперимента — действительно, всякий раз, когда нам указывают алгоритм, его можно перевести в форму программы машины Поста, приводящей к тому же результату.
2.4 Вопросы для самоконтроля
1) Понятие общей и конкретной проблемы по Посту;
2) Пространство символов и примитивные операции в машине Поста;
3) Понятие финитного 1-процесса в машине Поста;
4) Способы задания проблем и формулировка 1;
5) Гипотеза Поста;
3. МАШИНА ТЬЮРИНГА И АЛГОРИТМИЧЕСКИ НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ
3.1. Машина Тьюринга
Алан Тьюринг (Turing) в 1936 году опубликовал в трудах Лондонского математического общества статью «О вычислимых числах в приложении к проблеме разрешения», которая наравне с работами Поста и Черча лежит в основе современной теории алгоритмов.
Предыстория создания этой работы связана с формулировкой Давидом Гильбертом на Международном математическом конгрессе в Париже в 1900 году неразрешенных математических проблем. Одной из них была задача доказательства непротиворечивости системы аксиом обычной арифметики, которую Гильберт в дальнейшем уточнил как «проблему разрешимости» - нахождение общего метода, для определения выполнимости данного высказывания на языке формальной логики.
Статья Тьюринга как раз и давала ответ на эту проблему - вторая проблема Гильберта оказалась неразрешимой. Но значение статьи Тьюринга выходило далеко за рамки той задачи, по поводу которой она была написана.
Приведем характеристику этой работы, принадлежащую Джону Хопкрофту [4]: «Работая над проблемой Гильберта, Тьюрингу пришлось дать четкое определение самого понятия метода. Отталкиваясь от интуитивного представления о методе как о некоем алгоритме, т.е. процедуре, которая может быть выполнена механически, без творческого вмешательства, он показал, как эту идею можно воплотить в виде подробной модели вычислительного процесса. Полученная модель вычислений, в которой каждый алгоритм разбивался на последовательность простых, элементарных шагов, и была логической конструкцией, названной впоследствии машиной Тьюринга».
Машина Тьюринга является расширением модели конечного автомата, расширением, включающим потенциально бесконечную память с возможностью перехода (движения) от обозреваемой в данный момент ячейки к ее левому или правому соседу [4].
Формально машина Тьюринга может быть описана следующим образом:
Пусть заданы:
· конечное множество состояний – Q, в которых может находиться машина Тьюринга;
· конечное множество символов ленты – Γ;
· функция δ (функция переходов или программа), которая задается отображением пары из декартова произведения Q x Г (машина находится в состоянии qi и обозревает символ γi) в тройку декартова произведения Q х Г х {L,R} (машина переходит в состояние qj, заменяет символ γi на символ γj и передвигается влево или вправо на один символ ленты) – Q x Г→Q х Г х {L,R}
· один символ из Г→ е (пустой);
· подмножество Σ є Г → определяется как подмножество входных символов ленты, причем е є (Г-Σ);
· одно из состояний – q0 є Q является начальным состоянием машины.
 |
Решаемая проблема задается путем записи конечного количества символов из множества Σ є Г – Si є Σ на ленту:
после чего машина переводится в начальное состояние и головка устанавливается у самого левого непустого символа – (q0,↑ω), после чего в соответствии с указанной функцией переходов (qi, Si) →(qj, Sk, L или R) машина начинает заменять обозреваемые символы, передвигать головку вправо или влево и переходить в другие состояния, предписанные функций переходов.
Остановка машины происходит в том случае, если для пары (qi, Si) функция перехода не определена.
Алан Тьюринг высказал предположение, что любой алгоритм в интуитивном смысле этого слова может быть представлен эквивалентной машиной Тьюринга. Это предположение известно как тезис Черча–Тьюринга. Каждый компьютер может моделировать машину Тьюринга (операции перезаписи ячеек, сравнения и перехода к другой соседней ячейке с учетом изменения состояния машины). Следовательно, он может моделировать алгоритмы в любом формализме, и из этого тезиса следует, что все компьютеры (независимо от мощности, архитектуры и т.д.) эквивалентны с точки зрения принципиальной возможности решения алгоритмических задач.
3.2. Алгоритмически неразрешимые проблемы
За время своего существования человечество придумало множество алгоритмов для решения разнообразных практических и научных проблем. Зададимся вопросом – а существуют ли какие-нибудь проблемы, для которых невозможно придумать алгоритмы их решения?
Утверждение о существовании алгоритмически неразрешимых проблем является весьма сильным – мы констатируем, что мы не только сейчас на знаем соответствующего алгоритма, но мы не можем принципиально никогда его найти.
Успехи математики к концу XIX века привели к формированию мнения, которое выразил Д. Гильберт – «в математике не может быть неразрешимых проблем», в связи с этим формулировка проблем Гильбертом на конгрессе 1900 года в Париже была руководством к действию, констатацией отсутствия решений в данный момент.
Первой фундаментальной теоретической работой, связанной с доказательством алгоритмической неразрешимости, была работа Курта Гёделя – его известная теорема о неполноте символических логик. Это была строго формулированная математическая проблема, для которой не существует решающего ее алгоритма. Усилиями различных исследователей список алгоритмически неразрешимых проблем был значительно расширен. Сегодня принято при доказательстве алгоритмической неразрешимости некоторой задачи сводить ее к ставшей классической задаче – «задаче останова».
Имеет место быть следующая теорема (доказательство в [4]):
Теорема 3.1. Не существует алгоритма (машины Тьюринга), позволяющего по описанию произвольного алгоритма и его исходных данных (и алгоритм и данные заданы символами на ленте машины Тьюринга) определить, останавливается ли этот алгоритм на этих данных или работает бесконечно.
Таким образом, фундаментально алгоритмическая неразрешимость связана с бесконечностью выполняемых алгоритмом действий, т.е. невозможностью предсказать, что для любых исходных данных решение будет получено за конечное количество шагов.
Тем не менее, можно попытаться сформулировать причины, ведущие к алгоритмической неразрешимости, эти причины достаточно условны, так как все они сводимы к проблеме останова, однако такой подход позволяет более глубоко понять природу алгоритмической неразрешимости:
а) Отсутствие общего метода решения задачи
Проблема 1: Распределение девяток в записи числа π [10];
Определим функцию f(n) = i, где n – количество девяток подряд в десятичной записи числа π, а i – номер самой левой девятки из n девяток подряд:
π=3,141592… f(1) = 5.
Задача состоит в вычислении функции f(n) для произвольно заданного n.
Поскольку число π является иррациональным и трансцендентным, то мы не знаем никакой информации о распределении девяток (равно как и любых других цифр) в десятичной записи числа π. Вычисление f(n) связано с вычислением последующих цифр в разложении π, до тех пор, пока мы не обнаружим n девяток подряд, однако у нас нет общего метода вычисления f(n), поэтому для некоторых n вычисления могут продолжаться бесконечно – мы даже не знаем в принципе (по природе числа π) существует ли решение для всех n.
Проблема 2: Вычисление совершенных чисел;
Совершенные числа – это числа, которые равны сумме своих делителей, например: 28 = 1+2+4+7+14.
Определим функцию S(n) = n-ое по счёту совершенное число и поставим задачу вычисления S(n) по произвольно заданному n. Нет общего метода вычисления совершенных чисел, мы даже не знаем, множество совершенных чисел конечно или счетно, поэтому наш алгоритм должен перебирать все числа подряд, проверяя их на совершенность. Отсутствие общего метода решения не позволяет ответить на вопрос о останове алгоритма. Если мы проверили М чисел при поиске n-ого совершенного числа – означает ли это, что его вообще не существует?
Проблема 3: Десятая проблема Гильберта;
Пусть задан многочлен n -ой степени с целыми коэффициентами – P, существует ли алгоритм, который определяет, имеет ли уравнение P=0 решение в целых числах?
Ю.В. Матиясевич [4] показал, что такого алгоритма не существует, т.е. отсутствует общий метод определения целых корней уравнения P=0 по его целочисленным коэффициентам.
б) Информационная неопределенность задачи
Проблема 4: Позиционирование машины Поста на последний помеченный ящик [10];
Пусть на ленте машины Поста заданы наборы помеченных ящиков (кортежи) произвольной длины с произвольными расстояниями между кортежами и головка находится у самого левого помеченного ящика. Задача состоит установке головки на самый правый помеченный ящик последнего кортежа.
Попытка построения алгоритма, решающего эту задачу приводит к необходимости ответа на вопрос – когда после обнаружения конца кортежа мы сдвинулись вправо по пустым ящикам на М позиций и не обнаружили начало следующего кортежа – больше на ленте кортежей нет или они есть где-то правее? Информационная неопределенность задачи состоит в отсутствии информации либо о количестве кортежей на ленте, либо о максимальном расстоянии между кортежами – при наличии такой информации (при разрешении информационной неопределенности) задача становится алгоритмически разрешимой.
в) Логическая неразрешимость (в смысле теоремы Гёделя о неполноте)
Проблема 5: Проблема «останова» (см. теорема 3.1);
Проблема 6: Проблема эквивалентности алгоритмов;
По двум произвольным заданным алгоритмам (например, по двум машинам Тьюринга) определить, будут ли они выдавать одинаковые выходные результаты на любых исходных данных.
Проблема 7: Проблема тотальности;
По произвольному заданному алгоритму определить, будет ли он останавливаться на всех возможных наборах исходных данных. Другая формулировка этой задачи – является ли частичный алгоритм Р всюду определённым?
3.3. Проблема соответствий Поста над алфавитом Σ
В качестве более подробного примера алгоритмически неразрешимой задачи рассмотрим проблему соответствий Поста [1] (Э. Пост, 1943 г.). Мы выделили эту задачу, поскольку на первый взгляд она выглядит достаточно «алгоритмизуемой», однако она сводима к проблеме останова и является алгоритмически неразрешимой.
Постановка задачи:
Пусть дан алфавит Σ: |Σ| ≥ 2 (для одно-символьного алфавита задача имеет решение) и дано конечное множество пар из Σ+х Σ+, т.е. пары непустых цепочек произвольного языка над алфавитом Σ: (x1,y1), ……, (xm,ym).
Проблема: Выяснить существует ли конечная последовательность этих пар, не обязательно различных, такая что цепочка, составленная из левых подцепочек, совпадает с последовательностью правых подцепочек – такая последовательность называется решающей.
В качестве примера рассмотрим Σ = {a,b}
1. Входные цепочки: (abbb, b), (a, aab), (ba, b)
Решающая последовательность для этой задачи имеет вид:
(a,aab) (a,aab) (ba,b) (abbb,b), так как: a a ba abbb ≡ aab aab b b
2. Входные цепочки: (ab,aba), (aba,baa), (baa,aa)
Данная задача вообще не имеет решения, так как нельзя начинать с пары (aba,baa) или (baa,aa), поскольку не совпадают начальные символы подцепочек, но если начинать с цепочки (ab,aba), то в последующем не будет совпадать общее количество символов «а», т.к. в других двух парах количество символов «а» одинаково.
В общем случае мы можем построить частичный алгоритм, основанный на идее упорядоченной генерации возможных последовательностей цепочек (отметим, что мы имеем счетное множество таких последовательностей) с проверкой выполнения условий задачи. Если последовательность является решающей – то мы получаем результативный ответ за конечное количество шагов. Поскольку общий метод определения отсутствия решающей последовательности не может быть указан, т.к. задача сводима к проблеме «останова» и, следовательно, является алгоритмически неразрешимой, то при отсутствии решающей последовательности алгоритм порождает бесконечный цикл.
В теории алгоритмов такого рода проблемы, для которых может быть предложен частичный алгоритм их решения, частичный в том смысле, что он возможно, но не обязательно, за конечное количество шагов находит решение проблемы, называются частично разрешимыми проблемами.
В частности, проблема останова так же является частично разрешимой проблемой, а проблемы эквивалентности и тотальности не являются таковыми.
3.4 Вопросы для самоконтроля
1) Формальное описание машины Тьюринга;
2) Функция переходов в машине Тьюринга;
3) Понятие об алгоритмически неразрешимых проблемах
4) Проблема позиционирования в машине Поста;
5) Проблема соответствий Поста над алфавитом S;
6) Проблема останова в машине Тьюринга;
7) Проблема эквивалентности и тотальности;
4. ВВЕДЕНИЕ В АНАЛИЗ АЛГОРИТМОВ
4.1. Сравнительные оценки алгоритмов
При использовании алгоритмов для решения практических задач мы сталкиваемся с проблемой рационального выбора алгоритма решения задачи. Решение проблемы выбора связано с построением системы сравнительных оценок, которая в свою очередь существенно опирается на формальную модель алгоритма.
Будем рассматривать в дальнейшем, придерживаясь определений Поста, применимые к общей проблеме, правильные и финитные алгоритмы, т.е. алгоритмы, дающие 1-решение общей проблемы. В качестве формальной системы будем рассматривать абстрактную машину, включающую процессор с фон- Неймановской архитектурой, поддерживающий адресную память и набор «элементарных» операций соотнесенных с языком высокого уровня.
В целях дальнейшего анализа примем следующие допущения:
· каждая команда выполняется не более чем за фиксированное время;
· исходные данные алгоритма представляются машинными словами по b битов каждое.
Конкретная проблема задается N словами памяти, таким образом, на входе алгоритма – Nb = N*b бит информации. Отметим, что в ряде случаев, особенно при рассмотрении матричных задач N является мерой длины входа алгоритма, отражающей линейную размерность.
Программа, реализующая алгоритм для решения общей проблемы состоит из М машинных инструкций по bм битов – Мb = М*b м бит информации.
Кроме того, алгоритм может требовать следующих дополнительных ресурсов абстрактной машины:
· Sd – память для хранения промежуточных результатов;
· Sr – память для организации вычислительного процесса (память, необходимая для реализации рекурсивных вызовов и возвратов).
При решении конкретной проблемы, заданной N словами памяти алгоритм выполняет не более, чем конечное количество «элементарных» операций абстрактной машины в силу условия рассмотрения только финитных алгоритмов. В связи с этим введем следующее определение:
Определение 4.1. Трудоёмкость алгоритма.
Под трудоёмкостью алгоритма для данного конкретного входа – Fa(N), будем понимать количество «элементарных» операций совершаемых алгоритмом для решения конкретной проблемы в данной формальной системе.
Комплексный анализ алгоритма может быть выполнен на основе комплексной оценки ресурсов формальной системы, требуемых алгоритмом для решения конкретных проблем. Очевидно, что для различных областей применения веса ресурсов будут различны, что приводит к следующей комплексной оценке алгоритма:
yA=c1 * Fa(N) + c2 * M + c3 * Sd + c4 * Sr, где ci – веса ресурсов.
4.2 Система обозначений в анализе алгоритмов
При более детальном анализе трудоемкости алгоритма оказывается, что не всегда количество элементарных операций, выполняемых алгоритмом на одном входе длины N, совпадает с количеством операций на другом входе такой же длины. Это приводит к необходимости введения специальных обозначений, отражающих поведение функции трудоемкости данного алгоритма на входных данных фиксированной длины.
Пусть DА – множество конкретных проблем данной задачи, заданное в формальной системе. Пусть D Î DА – задание конкретной проблемы и |D| = N.
В общем случае существует собственное подмножество множества DА, включающее все конкретные проблемы, имеющие мощность N:
обозначим это подмножество через DN: DN = {DÎ DN,: |D| = N};
обозначим мощность множества DN через MDN → MDN = |DN |.
Тогда содержательно данный алгоритм, решая различные задачи размерности N, будет выполнять в каком-то случае наибольшее количество операций, а в каком-то случае наименьшее количество операций. Ведем следующие обозначения:
1. FaÙ(N) – худший случай – наибольшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:
|
2. FaÚ(N) – лучший случай – наименьшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:
|
3. ` Fa(N) – средний случай – среднее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерностью N:
|
4.3 Классификация алгоритмов по виду функции трудоёмкости
В зависимости от влияния исходных данных на функцию трудоемкости алгоритма может быть предложена следующая классификация, имеющая практическое значение для анализа алгоритмов:
1.Количественно-зависимые по трудоемкости алгоритмы
Это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений:
Fa (D) = Fa (|D|) = Fa (N)
Примерами алгоритмов с количественно-зависимой функцией трудоемкости могут служить алгоритмы для стандартных операций с массивами и матрицами – умножение матриц, умножение матрицы на вектор и т.д.
2.Параметрически-зависимые по трудоемкости алгоритмы
Это алгоритмы, трудоемкость которых определяется не размерностью входа (как правило, для этой группы размерность входа обычно фиксирована), а конкретными значениями обрабатываемых слов памяти:
Fa (D) = Fa (d1,…,dn) = Fa (P1,…,Pm), m £ n
Примерами алгоритмов с параметрически-зависимой трудоемкостью являются алгоритмы вычисления стандартных функций с заданной точностью путем вычисления соответствующих степенных рядов. Очевидно, что такие алгоритмы, имея на входе два числовых значения – аргумент функции и точность выполняют существенно зависящее от значений количество операций.
а) Вычисление xk последовательным умножением Þ Fa(x, k) = Fa (k).
б) Вычисление ex=å(xn/n!), с точностью до x Þ Fa = Fa (x, x)
3. Количественно-параметрические по трудоемкости алгоритмы
Однако в большинстве практических случаев функция трудоемкости зависит как от количества данных на входе, так и от значений входных данных, в этом случае:
Fa (D) = Fa (||D||, P1,…,Pm) = Fa (N, P1,…,Pm)
В качестве примера можно привести алгоритмы численных методов, в которых параметрически-зависимый внешний цикл по точности включает в себя количественно-зависимый фрагмент по размерности.
3.1 Порядково-зависимые по трудоемкости алгоритмы
Среди разнообразия параметрически-зависимых алгоритмов выделим еще оду группу, для которой количество операций зависит от порядка расположения исходных объектов.
Пусть множество D состоит из элементов (d1,…,dn), и ||D||=N,
Определим Dp = {(d1,…,dn)}- множество всех упорядоченных N-ок из d1,…,dn, отметим, что |Dp|=n!.
Если Fa (iDp) ¹ Fa (jDp), где iDp, jDp Î Dp, то алгоритм будем называть порядково-зависимым по трудоемкости.
Примерами таких алгоритмов могут служить ряд алгоритмов сортировки, алгоритмы поиска минимума и максимума в массиве. Рассмотрим более подробно алгоритм поиска максимума в массиве S, содержащим n элементов:
MaxS (S,n; Max)
Max S1
For i2 to n
if Max < Si
then Max Si (количество выполненных операций присваивания зависит от порядка следования элементов массива)
4.4 Асимптотический анализ функций
При анализе поведения функции трудоемкости алгоритма часто используют принятые в математике асимптотические обозначения, позволяющие показать скорость роста функции, маскируя при этом конкретные коэффициенты.
Такая оценка функции трудоемкости алгоритма называется сложностью алгоритма и позволяет определить предпочтения в использовании того или иного алгоритма для больших значений размерности исходных данных.
В асимптотическом анализе приняты следующие обозначения [6]:
1. Оценка Q (тетта)
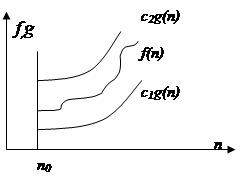Пусть f(n) и g(n) – положительные функции положительного аргумента, n ≥ 1 (количество объектов на входе и количество операций – положительные числа), тогда:
f(n) = Q (g(n)), если существуют
положительные с1, с2, n0, такие, что:
с1 * g(n) £ f(n) £ c2 * g(n), при n > n0
Обычно говорят, что при этом функция g(n) является асимптотически точной оценкой функции f(n), т.к. по определению функция f(n) не отличается от функции g(n) с точностью до постоянного множителя.
Отметим, что из f(n) = Q (g(n)) следует, что g(n) = Q (f(n)).
Примеры:
1) f(n)=4n2+nlnN+174 – f(n)= Q(n2);
2) f(n)=Q(1) – запись означает, что f(n) или равна константе, не равной нулю, или f(n) ограничена константой на ¥: f(n) = 7+1/n = Q(1).
2. Оценка О (О большое)
В отличие от оценки Q, оценка О требует только, что бы функция f(n) не превышала g(n) начиная с n > n0, с точностью до постоянного множителя:
 |
$ c > 0, n0 > 0:
0 £ f(n) £ c * g(n), "n > n0
Вообще, запись O(g(n)) обозначает класс функций, таких, что все они растут не быстрее, чем функция g(n) с точностью до постоянного множителя, поэтому иногда говорят, что g(n) мажорирует функцию f(n).
Например, для всех функций:
f(n)=1/n, f(n)= 12, f(n)=3*n+17, f(n)=n*Ln(n), f(n)=6*n2 +24*n+77
будет справедлива оценка О(n2 )
Указывая оценку О есть смысл указывать наиболее «близкую» мажорирующую функцию, поскольку например для f(n)= n2 справедлива оценка О(2n), однако она не имеет практического смысла.
3. Оценка W (Омега)
В отличие от оценки О, оценка W является оценкой снизу – т.е. определяет класс функций, которые растут не медленнее, чем g(n) с точностью до постоянного множителя:
 |
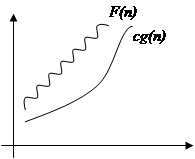$ c > 0, n0 >0:
0 £ c * g(n) £ f(n)
Например, запись W(n*Ln(n)) обозначает класс функций, которые растут не медленнее, чем g(n) = n*Ln(n), в этот класс попадают все полиномы со степенью большей единицы, равно как и все степенные функции с основанием большим единицы.
Асимптотическое обозначение О восходит к учебнику Бахмана по теории простых чисел (Bachman, 1892), обозначения Q, W введены Д. Кнутом- (Donald Knuth) [6].
Отметим, что не всегда для пары функций справедливо одно из асимптотических соотношений, например для f(n)=n1+sin(n) и g(n)=n не выполняется ни одно из асимптотических соотношений.
В асимптотическом анализе алгоритмов разработаны специальные методы получения асимптотических оценок, особенно для класса рекурсивных алгоритмов. Очевидно, что Q оценка является более прдпочтительной, чем оценка О. Знание асимптотики поведения функции трудоемкости алгоритма - его сложности, дает возможность делать прогнозы по выбору более рационального с точки зрения трудоемкости алгоритма для больших размерностей исходных данных.
4.5 Вопросы для самоконтроля
1) Формальная система языка высокого уровня;
2) Понятие трудоемкости алгоритма в формальном базисе;
3) Обобщенный критерий оценки качества алгоритма,
4) Система обозначений в анализе алгоритмов - худший, лучший и средний случаи;
5) Классификация алгоритмов по виду функции трудоемкости;
6) Примеры количественных и параметрически–зависимых алгоритмов;
7) Обозначения в асимптотическом анализе функций;
8) Примеры функций, не связанных асимптотическими обозначениями;
5. ТРУДОЕМКОСТЬ АЛГОРИТМОВ И ВРЕМЕННЫЕ ОЦЕНКИ
5.1. Элементарные операции в языке записи алгоритмов
Для получения функции трудоемкости алгоритма, представленного в формальной системе введенной абстрактной машины необходимо уточнить понятия «элементарных» операций, соотнесенных с языком высокого уровня.
В качестве таких «элементарных» операций предлагается использовать следующие:
1) Простое присваивание: а b;
2) Одномерная индексация a[i]: (адрес (a)+i *длинна элемента);
3) Арифметические операции: (*, /, -, +);
4) Операции сравнения: a < b;
5) Логические операции (l1) {or, and, not} (l2);
Опираясь на идеи структурного программирования, исключим команду перехода по адресу, считая ее связанной с операцией сравнения в конструкции ветвления.
После введения элементарных операций анализ трудоемкости основных алгоритмических конструкций в общем виде сводится к следующим положениям:
А) Конструкция «Следование»
Трудоемкость конструкции есть сумма трудоемкостей
блоков, следующих друг за другом.
F «следование» = f1 + … + fk, где k – количество блоков.
B) Конструкция «Ветвление»
if (l) then
fthen с вероятностью p
else
felse с вероятностью (1-p)
Общая трудоемкость конструкции «Ветвление» требует анализа вероятности выполнения переходов на блоки «Then» и «Else» и определяется как:
F «ветвление» = fthen * p + felse * (1-p).
C) Конструкция «Цикл»
for i 1 to N
Û
end
После сведения конструкции к элементарным операциям ее трудоемкость определяется как:
F «цикл» = 1+3*N+N*f«тела цикла»
5.2 Примеры анализа простых алгоритмов
Пример 1 Задача суммирования элементов квадратной матрицы
SumM (A, n; Sum)
Sum 0
For i 1 to n
For j 1 to n
Sum Sum + A[i,j]
end for
Return (Sum)
End
Алгоритм выполняет одинаковое количество операций при фиксированном значении n, и следовательно является количественно-зависимым. Применение методики анализа конструкции «Цикл» дает:
FA(n)=1+1+ n *(3+1+ n *(3+4))=7 n 2+4* n +2 = Q(n 2), заметим, что под n понимается линейная размерность матрицы, в то время как на вход алгоритма подается n 2 значений.
Пример 2 Задача поиска максимума в массиве
MaxS (S,n; Max)
Max S[1]
For i 2 to n
if Max < S[i]
then Max S[i]
end for
return Max
End
Данный алгоритм является количественно-параметрическим, поэтому для фиксированной размерности исходных данных необходимо проводить анализ для худшего, лучшего и среднего случая.
А). Худший случай
Максимальное количество переприсваиваний максимума (на каждом проходе цикла) будет в том случае, если элементы массива отсортированы по возрастанию. Трудоемкость алгоритма в этом случае равна:
FA^(n)=1+1+1+ (n-1) (3+2+2)=7 n - 4 = Q(n).
Б) Лучший случай
Минимальное количество переприсваивания максимума (ни одного на каждом проходе цикла) будет в том случае, если максимальный элемент расположен на первом месте в массиве. Трудоемкость алгоритма в этом случае равна:
FAÚ(n)=1+1+1+ (n-1) (3+2)=5 n - 2 = Q(n).
В) Средний случай
Алгоритм поиска максимума последовательно перебирает элементы массива, сравнивая текущий элемент массива с текущим значением максимума. На очередном шаге, когда просматривается к-ый элемент массива, переприсваивание максимума произойдет, если в подмассиве из первых к элементов максимальным элементом является последний. Очевидно, что в случае равномерного распределения исходных данных, вероятность того, что максимальный из к элементов расположен в определенной (последней) позиции равна 1/к. Тогда в массиве из n элементов общее количество операций переприсваивания максимума определяется как:
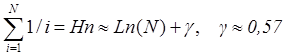
Величина Hn называется n-ым гармоническим числом. Таким образом, точное значение (математическое ожидание) среднего количества операций присваивания в алгоритме поиска максимума в массиве из n элементов определяется величиной Hn (на бесконечности количества испытаний), тогда:
`FA(n)=1 + (n-1) (3+2) + 2 (Ln(n) + g)=5 n +2 Ln(n) - 4 +2 g = Q(n).
5.3. Переход к временным оценкам
Сравнение двух алгоритмов по их функции трудоемкости вносит некоторую ошибку в получаемые результаты. Основной причиной этой ошибки является различная частотная встречаемость элементарных операций, порождаемая разными алгоритмами и различие во временах выполнения элементарных операций на реальном процессоре. Таким образом, возникает задача перехода от функции трудоемкости к оценке времени работы алгоритма на конкретном процессоре:
Дано: FA(DA) - трудоёмкость алгоритма требуется определить время работы программной реализации алгоритма – TA(DA).
На пути построения временных оценок мы сталкиваемся с целым набором различных проблем, пофакторный учет которых вызывает существенные трудности. Укажем основные из этих проблем:
· неадекватность формальной системы записи алгоритма и реальной системы команд процессора;
· наличие архитектурных особенностей существенно влияющих на наблюдаемое время выполнения программы, таких как конвейер, кеширование памяти, предвыборка команд и данных, и т.д.;
· различные времена выполнения реальных машинных команд;
· различие во времени выполнения одной команды, в зависимости от значений операндов
· различные времена реального выполнения однородных команд в зависимости от типов данных;
· неоднозначности компиляции исходного текста, обусловленные как самим компилятором, так и его настройками.
Попытки различного подхода к учету этих факторов привели к появлению разнообразных методик перехода к временным оценкам.
1) Пооперационный анализ
Идея пооперационного анализа состоит в получении пооперационной функции трудоемкости для каждой из используемых алгоритмом элементарных операций с учетом типов данных. Следующим шагом является экспериментальное определение среднего времени выполнения данной элементарной операции на конкретной вычислительной машине. Ожидаемое время выполнения рассчитывается как сумма произведений пооперационной трудоемкости на средние времена операций:
TA(N) = å Faопi(N) * `t опi
2) Метод Гиббсона
Метод предполагает проведение совокупного анализа по трудоемкости и переход к временным оценкам на основе принадлежности решаемой задачи к одному из следующих типов:
· задачи научно-технического характера с преобладанием операций с операндами действительного типа;
· задачи дискретной математики с преобладанием операций с операндами целого типа
· задачи баз данных с преобладанием операций с операндами строкового типа
 |
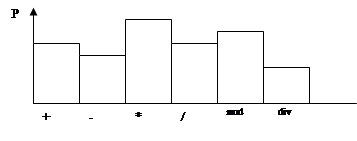Далее на основе анализа множества реальных программ для решения соответствующих типов задач определяется частотная встречаемость операций (рис 5.1), создаются соответствующие тестовые программы, и определяется среднее время на операцию в данном типе задач –` t тип задачи.
Рис 5.1 Возможный вид частотной встречаемости операций
На основе полученной информации оценивается общее время работы алгоритма в виде:
TA(N) = FA(N) *`t тип задачи
3) Метод прямого определения среднего времени
В этом методе так же проводится совокупный анализ по трудоемкости – определяется FA(N), после чего на основе прямого эксперимента для различных значений N э определяется среднее время работы данной программы Tэ и на основе известной функции трудоемкости рассчитывается среднее время на обобщенную элементарную операцию, порождаемое данным алгоритмом, компилятором и компьютером – ` tа. Эти данные могут быть (в предположении об устойчивости среднего времени по N) интерполированы или экстраполированы на другие значения размерности задачи следующим образом:
`tа= Tэ(Nэ) / FA(Nэ), T(N) = `tа * FA(N).
5.4 Пример пооперационного временного анализа
В ряде случаев именно пооперационный анализ позволяет выявить тонкие аспекты рационального применения того или иного алгоритма решения задачи. В качестве примера рассмотрим задачу умножения двух комплексных чисел:
(a+bi)*(c+di)=(ac - bd) + i(ad + bc)=e + if
1. Алгоритм А1 (прямое вычисление e, f – четыре умножения)
|
ea*c - b*d
¦a*d + b*c
Return (e, ¦)
End.
2. Алгоритм А2 (вычисление e, f за три умножения)
MultComplex2 (a, b, c, d; e, f)
z1c*(a + b)
|
z3a*(d - c)
ez1 - z2
¦z1 + z3
Return (e, ¦)
End.
Пооперационный анализ этих двух алгоритмов не представляет труда, и его результаты приведены справа от записи соответствующих алгоритмов.
По совокупному количеству элементарных операций алгоритм А2 уступает алгоритму А1, однако в реальных компьютерах операция умножения требует большего времени, чем операция сложения, и можно путем пооперационного анализа ответить на вопрос: при каких условиях алгоритм А2 предпочтительнее алгоритма А1?
Введем параметры q и r, устанавливающие соотношения между временами выполнения операции умножения, сложения и присваивания для операндов действительного типа.
Тогда мы можем привести временные оценки двух алгоритмов к времени выполнения операции сложения/вычитания – t+:
t* = q*t+, q>1;
t=r*t+, r<1, тогда приведенные к t+ временные оценки имеют вид:
ТA1 = 4*q*t++2*t++2*r*t+=t+*(4*q+2+2*r);
ТA2 = 3*q*t++5*t++5*r*t+=t+*(3*q+5+5*r).
Равенство времен будет достигнуто при условии:
4*q+2+2*r = 3*q+5+5*r, откуда:
q = 3 + 3r и следовательно при q > 3 + 3r алгоритм А2 будет работать более эффективно.
Таким образом, если среда реализации алгоритмов А1 и А2 – язык программирования, обслуживающий его компилятор и компьютер на котором реализуется задача – такова, что время выполнения операции умножения двух действительных чисел более чем втрое превышает время сложения двух действительных чисел, в предположении, что r<< 1, а это реальное соотношение, то для реализации более предпочтителен алгоритм А2.
Конечно, выигрыш во времени пренебрежимо мал, если мы перемножаем только два комплексных числа, однако, если этот алгоритм является частью сложной вычислительной задачи с комплексными числами, требующей существенно значимого по времени количества умножений, то выигрыш во времени может быть ощутим. Оценка такого выигрыша на одно умножение комплексных чисел следует из только что проведенного анализа:
DT = (q – 3 – 3*r)* t+
5.5 Вопросы для самоконтроля
1) Элементарные операции в псевдоязыке высокого уровня;
2) Анализ трудоемкости основных алгоритмических конструкций;
3) Построение функции трудоемкости для суммирования матрицы;
4) Построение функции трудоемкости для задачи поиска максимума;
5) Проблемы при переходе от трудоемкости к временным оценкам;
6) Методики перехода от функции трудоемкости к временным оценкам;
7) Возможности пооперационного анализа алгоритмов на примере задачи умножения комплексных чисел;
6. ТЕОРИЯ СЛОЖНОСТИ ВЫЧИСЛЕНИЙ И СЛОЖНОСТНЫЕ КЛАССЫ ЗАДАЧ
6.1 Теоретический предел трудоемкости задачи
Рассматривая некоторую алгоритмически разрешимую задачу, и анализируя один из алгоритмов ее решения, мы можем получить оценку трудоемкости этого алгоритма в худшем случае – ¦ˆA(DA)=O(g(DA)). Такие же оценки мы можем получить и для других известных алгоритмов решения данной задачи. Рассматривая задачу с этой точки зрения, возникает резонный вопрос – а существует ли функциональный нижний предел для g(DA) и если «да», то существует ли алгоритм, решающий задачу с такой трудоемкостью в худшем случае.
Другая, более точная формулировка, имеет следующий вид: какова оценка сложности самого «быстрого» алгоритма решения данной задачи в худшем случае? Очевидно, что это оценка самой задачи, а не какого либо алгоритма ее решения. Таким образом, мы приходим к определению понятия функционального теоретического нижнего предела трудоемкости задачи в худшем случае:
Fthlim= min { Q (Fa^ (D)) }
Если мы можем на основе теоретических рассуждений доказать существование и получить оценивающую функцию, то мы можем утверждать, что любой алгоритм, решающий данную задачу работает не быстрее, чем с оценкой Fthlim в худшем случае:
Fa^ (D) = W (Fthlim)
Приведем ряд примеров:
1) Задача поиска максимума в массиве A=(a1,…,an) – для этой задачи, очевидно должны быть просмотрены все элементы, и Fthlim=Q (n).
2) Задача умножения матриц - для этой задачи можно сделать предположение, что необходимо выполнить некоторые арифметические операции со всеми исходными данными, теоретическое обоснование какой–либо другой оценки на сегодня не известно [6], что приводит нас к оценке Fthlim=Q (n2). Отметим, что лучший алгоритм умножения м
