Пусть для изучения генеральной совокупности относительно количественного признака Х произведена выборка объёма n.
Выборочной средней  называется среднее арифметическое значение выборки.
называется среднее арифметическое значение выборки.
Если все значения х1, х2, …, хn выборки различны, то
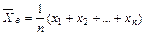 | (7.1) |
Если же значения признака х1, х2, …, хk имеют соответственно частоты n1,n2,…,nk , причем n1+n2+…+nk=n, то
 | (7.2) |
Иногда бывает целесообразным выборочные значения случайной величины разбить на отдельные группы. Для каждой группы можно найти её среднюю.
Групповой средней  называется среднее арифметическое значений выборки, принадлежащих группе.
называется среднее арифметическое значений выборки, принадлежащих группе.
По групповым средним можно найти среднее для всей выборки.
Общей средней  называется среднее арифметическое значение групповых средних.
называется среднее арифметическое значение групповых средних.
Пример 7.1. Найти общую среднюю на основе выборки.
| Группа | 1 | 2 | |||
| Значение варианты | 2 | 5 | 1 | 4 | 7 |
| Частота | 10 | 15 | 15 | 20 | 25 |
| объем | 25 | 60 | |||
Решение: Находим групповые средние:
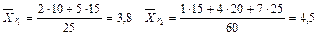
Общая средняя

Если варианты хi – большие числа, то для облегчения вычисления выборочной средней используют следующий приём. Пусть С – константа.
Так как
 , то формула (7.1) преобразуется к виду:
, то формула (7.1) преобразуется к виду:
 | (7.3) |
Константу С (так называемый ложный нуль) берут такой, чтобы во-первых, разности хi -C были небольшими и, во-вторых, число С было по возможности целым.
Пример 7.2. Имеется выборка:
| х1=71,88 | х2=71,93 | х3=72,05 | х4=72,07 | х5=71,90 |
| х6=72,02 | х7=71,93 | х8=71,77 | х9=71,77 | х10=71,96 |
Найти выборочную среднюю.
Решение: Берем С =72 и вычисляем разности 
| α1=-0,12 | α2=-0,07 | α3=0,05 | α4=0,07 | α5=-0,10 |
| α6=0,02 | α7=-0,07 | α8=-0,23 | α9=0,11 | α10=-0,04 |
Их сумма: α1+α2+…+α10=-0,38; их среднее арифметическое:  ; выборочная средняя:
; выборочная средняя:  .
.
Для того, чтобы охарактеризовать рассеяние наблюдаемых значений количественного признака выборки относительно выборочного среднего вводят понятие выборочной дисперсии.
Выборочной дисперсией Dв называется среднее арифметическое квадратов отклонений наблюдаемых значений признака Х от выборочной средней  .
.
Если все значения х1, х2, …, хn признака выборки объёма n различны, то
 | (7.4) |
Если же значения признака х1, х2, …, хk имеют соответственно частоты n1,n2,…,nk, причем n1+n2+…+nk=n, то
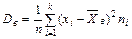 | (7.5) |
Пример 7.3. Выборочная совокупность задана таблицей распределения:
| xi | 1 | 2 | 3 | 4 |
| ni | 20 | 15 | 10 | 5 |
Найти выборочную дисперсию.
Решение: Согласно формулам (7.2) и (7.5) имеем:
 .
.
Выборочным средним квадратическим отклонением называется квадратный корень из выборочной дисперсии: 
Можно доказать, что
 | (7.6) |
Так как М(Dв)¹Dr, то выборочная дисперсия Dв является смещенной оценкой генеральной дисперсии Dr. Чтобы получить несмещенную оценку генеральной дисперсии Dr , вводят понятие так называемой исправленной (эмпирической) дисперсии S2, которая определяется формулой:
 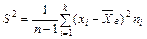 | (7.7) |
Исправленная дисперсия (7.7) является несмещенной оценкой генеральной дисперсии
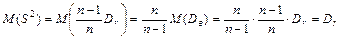 |
Если варианты хi – большие числа, то для облегчения вычисления выборочной дисперсии Dв формулу (7.4) преобразуют к следующему виду:
 | (7.8) |
где С – ложный нуль.
Пример 7.4. Через каждый час измерялось напряжение тока в электросети. Результаты измерений в вольтах представлены в таблице 7.1:
Таблица 7.1
| i | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| xi | 222 | 219 | 224 | 220 | 218 | 217 | 221 | 220 | 215 | 218 | 223 | 225 |
| i | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| xi | 220 | 226 | 221 | 216 | 211 | 219 | 220 | 221 | 222 | 218 | 221 | 219 |
Найти оценки для математического ожидания и дисперсии результатов измерений.
Решение: Оценки для математического ожидания и дисперсии найдем по формулам (7.3) и (7.8), положив С =220. Все необходимые вычисления приведены в таблице 7.2:
Таблица 7.2
| i | xi-C | (xi-C)2 | i | xi-C | (xi-C)2 | i | xi-C | (xi-C)2 |
| 1 | 2 | 4 | 9 | -5 | 25 | 17 | 1 | 1 |
| 2 | -1 | 1 | 10 | -2 | 4 | 18 | -1 | 1 |
| 3 | 4 | 16 | 11 | 3 | 9 | 19 | 0 | 0 |
| 4 | 0 | 0 | 12 | 5 | 25 | 20 | 1 | 1 |
| 5 | -2 | 4 | 13 | 0 | 0 | 21 | 2 | 4 |
| 6 | -3 | 9 | 14 | 6 | 36 | 22 | -2 | 4 |
| 7 | 1 | 1 | 15 | 1 | 1 | 23 | 1 | 1 |
| 8 | 0 | 0 | 16 | -4 | 16 | 24 | -1 | 1 |
| Σ | 1 | 35 | 4 | 116 | 1 | 13 |
Следовательно,

 2020-04-12
2020-04-12 6081
6081
