Факультет информатики
Кафедра информационных систем
ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ
для студентов 1 курса (2 семестр) специальностей: «Информатика», «Профессиональное обучение (экономика и управление)»
дневного отделения
тема «Поверхности 2-го порядка
Составила ст. преподаватель
кафедры ИС, к. ф.-м. н
Арапина-Арапова Е.С.
2008 г.
Индивидуальное задание
для студентов 1 курса (2 семестр) специальностей «Информатика», «Профессиональное обучение (экономика и управление)»
тема «Поверхности 2-го порядка».
I. Задания.
Установить тип поверхности и построить ее.
1.  2.
2.  3.
3.  4.
4.  5.
5. 
| 6.  7.
7.  8.
8.  9.
9. 
|
(Значения чисел a, b, c, p смотреть в таблице ниже. Выполняется задание по вариантам. Номер варианта выбирается по списку в журнале).
Варианты
| Номер варианта | a | b | c | p | Номер варианта | a | b | c | p | |
| 1 | 2 | 3 | 4 | 2 | 21 | 4 | 3 | 2 | 2 | |
| 2 | 2 | 4 | 3 | 2 | 22 | 4 | 2 | 3 | 2 | |
| 3 | 4 | 3 | 2 | 2 | 23 | 3 | 4 | 2 | 2 | |
| 4 | 4 | 2 | 3 | 2 | 24 | 3 | 2 | 4 | 2 | |
| 5 | 3 | 4 | 2 | 2 | 25 | 3 | 4 | 5 | 1 | |
| 6 | 3 | 2 | 4 | 2 | 26 | 3 | 5 | 4 | 1 | |
| 7 | 3 | 4 | 5 | 1 | 27 | 4 | 3 | 5 | 1 | |
| 8 | 3 | 5 | 4 | 1 | 28 | 4 | 5 | 3 | 1 | |
| 9 | 4 | 3 | 5 | 1 | 29 | 5 | 3 | 4 | 1 | |
| 10 | 4 | 5 | 3 | 1 | 30 | 5 | 4 | 3 | 1 | |
| 11 | 5 | 3 | 4 | 1 | 31 | 1 | 2 | 3 | 2 | |
| 12 | 5 | 4 | 3 | 1 | 32 | 1 | 3 | 2 | 2 | |
| 13 | 1 | 2 | 3 | 2 | 33 | 3 | 2 | 1 | 2 | |
| 14 | 1 | 3 | 2 | 2 | 34 | 3 | 1 | 2 | 2 | |
| 15 | 3 | 2 | 1 | 2 | 35 | 2 | 3 | 1 | 2 | |
| 16 | 3 | 1 | 2 | 2 | 36 | 2 | 1 | 3 | 2 | |
| 17 | 2 | 3 | 1 | 2 | 37 | 2 | 3 | 4 | 2 | |
| 18 | 2 | 1 | 3 | 2 | 38 | 2 | 4 | 3 | 2 | |
| 19 | 2 | 3 | 4 | 2 | 39 | 4 | 3 | 2 | 2 | |
| 20 | 2 | 4 | 3 | 2 | 40 | 4 | 2 | 3 | 2 |
|
|
|
II. Теоретический материал.
Кривые второго порядка (на плоскости)
Эллипс.
Эллипсом называется геометрическое место точек плоскости, для которых сумма расстояний до двух фиксированных точек плоскости  и
и  , называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
, называемых фокусами, есть величина постоянная, большая, чем расстояние между фокусами.
Постоянную сумму расстояний произвольной точки эллипса до фокусов принято обозначать через  . Расстояние между фокусами равно
. Расстояние между фокусами равно  .
.
Если фокусы эллипса совпадают, то он представляет собой окружность.
Расположим эллипс так, чтобы его фокусы лежали на оси абсцисс симметрично относительно оси ординат, то есть  (Рис.1). Пусть
(Рис.1). Пусть  текущая точка эллипса. В этой системе координат уравнение эллипса имеет вид:
текущая точка эллипса. В этой системе координат уравнение эллипса имеет вид:
 , (1)
, (1)
где  - большая,
- большая,  - малая полуоси эллипса,
- малая полуоси эллипса,  . Центр симметрии эллипса, определяемого уравнением (2.12.1), совпадает с началом координат. Уравнение вида (1) называется каноническим уравнением эллипса. Это уравнение второй степени, следовательно, эллипс – кривая второго порядка.
. Центр симметрии эллипса, определяемого уравнением (2.12.1), совпадает с началом координат. Уравнение вида (1) называется каноническим уравнением эллипса. Это уравнение второй степени, следовательно, эллипс – кривая второго порядка.

Рис.1.
Эксцентриситетом эллипса называется число  , равное отношению фокусного расстояния к большой полуоси эллипса. Для эллипса -
, равное отношению фокусного расстояния к большой полуоси эллипса. Для эллипса -  (для окружности -
(для окружности -  ). Отрезки
). Отрезки  и
и  называются фокальными радиусами точки М и могут быть вычислены по формулам
называются фокальными радиусами точки М и могут быть вычислены по формулам  и
и  . Если эллипс определен уравнением (1) и
. Если эллипс определен уравнением (1) и  , то прямые
, то прямые  называются директрисами эллипса (если
называются директрисами эллипса (если  , то директрисы определяются уравнениями
, то директрисы определяются уравнениями  ).
).
|
|
|
Гипербола.
Гиперболой называется геометрическое место точек плоскости, для каждой из которых абсолютное значение разности расстояний до двух данных точек плоскости  и
и  , называемых фокусами, есть величина постоянная, равная
, называемых фокусами, есть величина постоянная, равная  .
.
Расстояние между фокусами равно  .
.
При указанном выборе системы координат оси координат являются осями симметрии гиперболы, а начало координат – ее центром симметрии. Ось  называется
называется

Рис. 2.
действительной осью, а  - мнимой осью гиперболы. Точки пересечения гиперболы с осью называются вершинами гиперболы.
- мнимой осью гиперболы. Точки пересечения гиперболы с осью называются вершинами гиперболы.
В этой системе координат каноническое уравнение гиперболы имеет вид:
 (2)
(2)
Эксцентриситетом гиперболы (как и эллипса) называется число  , где
, где  - расстояние от центра гиперболы до ее вершины. Очевидно, что для любой гиперболы
- расстояние от центра гиперболы до ее вершины. Очевидно, что для любой гиперболы  .
.
Если  - произвольная точка гиперболы, то отрезки
- произвольная точка гиперболы, то отрезки  и
и  называются фокальными радиусами точки М. Фокальные радиусы правой ветви гиперболы могут быть вычислены по формулам
называются фокальными радиусами точки М. Фокальные радиусы правой ветви гиперболы могут быть вычислены по формулам  и
и  . Фокальные радиусы левой ветви гиперболы – по формулам
. Фокальные радиусы левой ветви гиперболы – по формулам  и
и  .
.
Парабола.
Параболой называется геометрическое место точек плоскости, для каждой из которых расстояние до некоторой фиксированной точки плоскости  , называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.
, называемой фокусом, равно расстоянию до некоторой фиксированной прямой, называемой директрисой.

Рис. 2.14.1
Парабола имеет одну ось симметрии, называемую осью параболы, с которой она пересекается в единственной точке. Точка, в которой парабола пересекается с осью симметрии, называется вершиной параболы. При указанном выше выборе системы координат ось параболы совмещена с осью абсцисс, вершина находится в начале координат, а вся парабола лежит в правой полуплоскости.
В этой системе координат каноническое уравнение параболы имеет вид:
 (3)
(3)
Поверхности второго порядка (в пространстве)






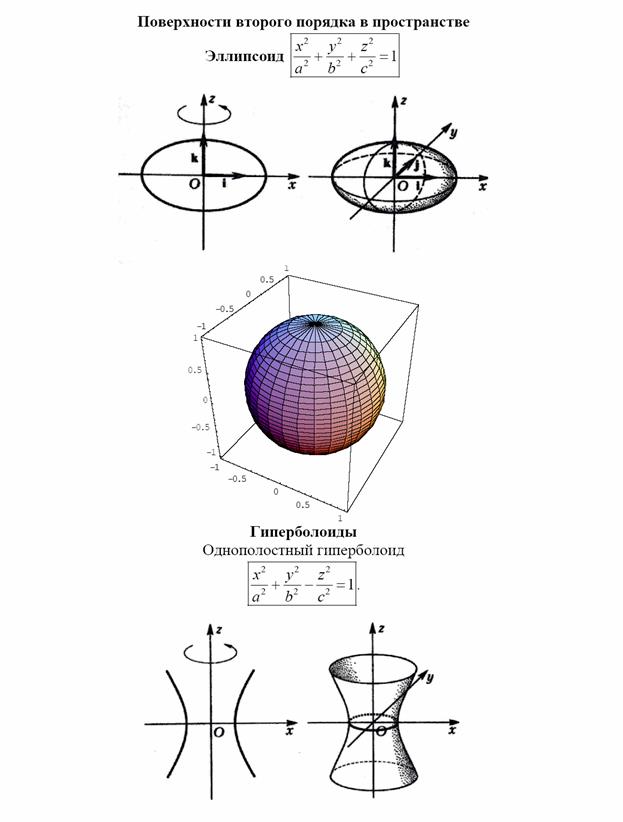
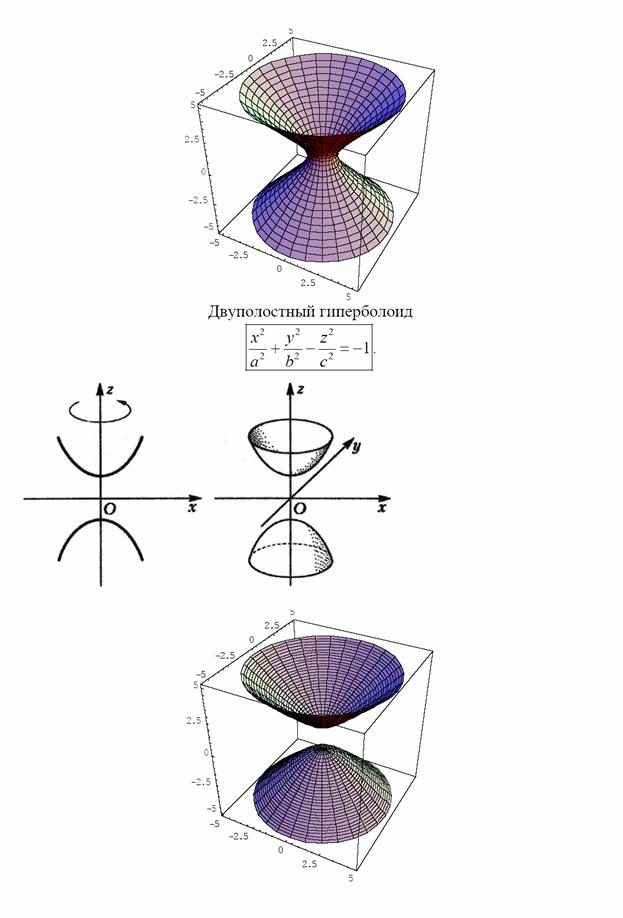






 2020-08-05
2020-08-05 411
411






