от произвольных функций
В предыдущем параграфе рассматривались признаки сходимости (признаки сравнения) несобственных интегралов 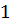 рода
рода  от положительных (или отрицательных) функций
от положительных (или отрицательных) функций 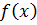 .
.
Если функция 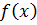 , начиная с какого - то места
, начиная с какого - то места  , имеет значения одного знака
, имеет значения одного знака  , то на промежутке
, то на промежутке 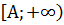 эта функция является положительной (или отрицательной), и для исследования сходимости несобственного интеграла
эта функция является положительной (или отрицательной), и для исследования сходимости несобственного интеграла  , а значит и
, а значит и  , также можно применять признаки сравнения.
, также можно применять признаки сравнения.
Если же подынтегральная функция не сохраняет знак ни на каком промежутке вида  , где
, где  , то эти признаки сходимости уже не применимы.
, то эти признаки сходимости уже не применимы.
В этом параграфе рассматриваются несобственные интегралы 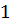 рода
рода  , где функция
, где функция 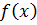 является знакопеременной при
является знакопеременной при  , т.е. на любом промежутке вида
, т.е. на любом промежутке вида 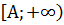 , где
, где  , функция
, функция 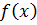 меняет знак (как, например, функция
меняет знак (как, например, функция 
 или
или  ).
).
Абсолютная сходимость несобственных интегралов.
Определение. Несобственный интеграл  называется абсолютно сходящимся, если сходится несобственный интеграл
называется абсолютно сходящимся, если сходится несобственный интеграл  .
.
Для положительных функций 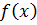 понятие сходимости несобственного интеграла от этих функций совпадает с понятием абсолютной сходимости, т.к.
понятие сходимости несобственного интеграла от этих функций совпадает с понятием абсолютной сходимости, т.к.  "
"  .
.
|
|
|
Что можно сказать о сходимости несобственного интеграла  ,
,
если известно, что он сходится абсолютно? Ответ на этот вопрос дает следующее утверждение.
Теорема. Абсолютно сходящийся несобственный интеграл – сходится. Другими словами:
если  – сходится абсолютно, то
– сходится абсолютно, то  – сходится.
– сходится.
Доказательство.
Имеем неравенства:


 "
"  ⇒
⇒ 

 ∙
∙  "
"  .
.
Так как интеграл  - сходится, то по свойству линейности интеграл
- сходится, то по свойству линейности интеграл  ∙
∙  - также сходится.
- также сходится.
Для положительных функций  и
и  ∙
∙  можно применить первый признак сравнения о сходимости несобственных интегралов:
можно применить первый признак сравнения о сходимости несобственных интегралов:
 - сходится ⇒
- сходится ⇒  - сходится.
- сходится.
Так как 
 , то из сходимости интегралов
, то из сходимости интегралов
 и
и  по свойству линейности следует
по свойству линейности следует
сходимость интеграла  . Теорема доказана.
. Теорема доказана.
Замечание. Обратное утверждение неверно, т.е. из сходимости несобственного интеграла не следует его абсолютная сходимость. Это означает, что абсолютная сходимость - более сильное свойство, чем просто сходимость. Подробнее об этом изложено чуть ниже.
Рассмотрим некоторые свойства абсолютно сходящихся интегралов.
Теорема 1. Пусть 
 "
"  , где
, где  . Тогда
. Тогда
если  - сходится, то
- сходится, то  - сходится абсолютно.
- сходится абсолютно.
Доказательство.
Для положительных функций  и
и  можно применить первый признак сравнения о сходимости несобственных интегралов:
можно применить первый признак сравнения о сходимости несобственных интегралов:
 - сходится ⇒
- сходится ⇒  - сходится.
- сходится.
Это означает, что интеграл  - сходится абсолютно
- сходится абсолютно
(по определению). Терема доказана.
Теорема 2. Рассмотрим несобственный интеграл  ,
,
|
|
|
где  - ограниченная функция на промежутке
- ограниченная функция на промежутке  .
.
Пусть несобственный интеграл  - сходится абсолютно. Тогда несобственный интеграл
- сходится абсолютно. Тогда несобственный интеграл  - также сходится абсолютно.
- также сходится абсолютно.
Доказательство.
Так как  - ограниченная функция, то
- ограниченная функция, то 
 "
"  для некоторого числа
для некоторого числа  . Следовательно:
. Следовательно:
 ∙
∙ 
 ∙
∙  "
"  .
.
Далее:  - сходится ⇒
- сходится ⇒  – сходится (по свойству линейности) ⇒
– сходится (по свойству линейности) ⇒  – сходится (первый признак сравнения) ⇒
– сходится (первый признак сравнения) ⇒  - сходится абсолютно. Теорема доказана.
- сходится абсолютно. Теорема доказана.
Пример.
Покажем, что  ,
,  - сходятся абсолютно "
- сходятся абсолютно "  .
.
Действительно, имеем:  "
"  ;
;
 - сходится, т.к.
- сходится, т.к.  ; следовательно,
; следовательно,
по Теореме 1 несобственный интеграл  - сходится абсолютно. Аналогичный факт имеем и для несобственного интеграла
- сходится абсолютно. Аналогичный факт имеем и для несобственного интеграла  .
.
Пример.
Покажем, что несобственные интегралы:  ,
,  , где
, где  ,
,  ,
,  - сходятся абсолютно.
- сходятся абсолютно.
Пусть 
 ,
,  или
или  ;
;
 - ограниченная функция на промежутке
- ограниченная функция на промежутке  . Так как
. Так как 


 – это сходящийся «эталонный» интеграл (
– это сходящийся «эталонный» интеграл (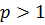 ), то по Теореме 2 несобственный интеграл
), то по Теореме 2 несобственный интеграл

 - сходится абсолютно.
- сходится абсолютно.
Условная сходимость несобственных интегралов.
Определение. Несобственный интеграл  называется условно сходящимся, если этот интеграл сходится, а интеграл от модуля функции:
называется условно сходящимся, если этот интеграл сходится, а интеграл от модуля функции:  - расходится.
- расходится.
Другими словами, если несобственный интеграл  - сходится, но абсолютной сходимости этого интеграла – нет, то такой интеграл называется условно сходящимся.
- сходится, но абсолютной сходимости этого интеграла – нет, то такой интеграл называется условно сходящимся.
Примерами условно сходящихся несобственных интегралов будут интегралы Дирихле:
 ,
,  , где
, где  .
.
Покажем это.
Применим к этим интегралам формулу интегрирования по частям.





 ;
;





 .
.
Несобственные интегралы  и
и  – это частные случаи рассмотренных выше интегралов вида
– это частные случаи рассмотренных выше интегралов вида  ,
,  .
.
Эти интегралы сходятся (абсолютно), т.к.  (
(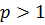 ). Следовательно, интегралы Дирихле:
). Следовательно, интегралы Дирихле:  ,
,  , (
, ( ) - также сходятся.
) - также сходятся.
Теперь покажем, что абсолютной сходимости этих интегралов - нет, т.е. что интегралы:  ,
,  - расходятся.
- расходятся.
Рассмотрим интеграл  . Предположим, что он сходится. Так как
. Предположим, что он сходится. Так как  "
"  , то по первому признаку сравнения сходится и интеграл
, то по первому признаку сравнения сходится и интеграл 
 ; кроме того, как показано выше, сходится и интеграл
; кроме того, как показано выше, сходится и интеграл 
 .
.
Тогда сумма двух сходящихся интегралов по свойству линейности также сходится:
 , но интеграл
, но интеграл  , как известно, расходится.
, как известно, расходится.
Полученное противоречие показывает, что на самом деле несобственный интеграл  - расходится. Аналогично доказывается, что
- расходится. Аналогично доказывается, что  - расходится.
- расходится.
Таким образом, доказано, что интегралы Дирихле сходятся условно.
Очевидно, что сходятся условно и интегралы вида:
 ,
,  , где
, где  ,
,  ,
,  .
.
Замечание. Вместо несобственного интеграла  , где
, где  - можно рассмотреть несобственный интеграл
- можно рассмотреть несобственный интеграл  , который также сходится условно. Действительно:
, который также сходится условно. Действительно: 
 , а интеграл
, а интеграл  - является собственным (определенным) интегралом, так как подынтегральная функция
- является собственным (определенным) интегралом, так как подынтегральная функция 
 - ограничена на
- ограничена на 
 .
.
Замечание. Используя сходимость интегралов Дирихле, вводятся неэлементарные функции интегральный синус  и интегральный косинус
и интегральный косинус  :
:

 ,
, 
 ,
,  .
.
Значения этих функций задаются в специальных таблицах.
Условная сходимость некоторых несобственных интегралов вида
 - может быть установлена с помощью признаков Абеля и Дирихле, которые мы приведем без доказательства.
- может быть установлена с помощью признаков Абеля и Дирихле, которые мы приведем без доказательства.
Теорема (признак Абеля).
Пусть выполнены следующие условия:
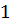 ) несобственный интеграл
) несобственный интеграл  - сходится (условно или абсолютно);
- сходится (условно или абсолютно);
 ) функция
) функция  - монотонна и ограничена на промежутке
- монотонна и ограничена на промежутке  .
.
Тогда несобственный интеграл  - сходится.
- сходится.
Теорема (признак Дирихле).
Пусть выполнены следующие условия:
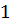 ) интегралы
) интегралы  - ограничены при значениях
- ограничены при значениях  ;
;
 ) функция
) функция  - монотонна и стремится к нулю при
- монотонна и стремится к нулю при  .
.
Тогда несобственный интеграл  - сходится.
- сходится.
Замечание. В признаке Дирихле первое условие - более слабое, чем в признаке Абеля, так как в нем не требуется сходимость несобственного интеграла  ; но второе условие - более сильное, так как вместо ограниченности функции
; но второе условие - более сильное, так как вместо ограниченности функции  требуется стремление ее к нулю при
требуется стремление ее к нулю при  .
.
|
|
|
Пример. Рассмотрим несобственные интегралы:
 ,
,  , где
, где  ,
,  ,
,  ,
,  .
.
Применим признак Дирихле.
Здесь  или
или  ,
,  ;
;  при
при  .
.
 или
или  .
.
 ∙
∙  ∙
∙  ;
;
 ∙
∙  ⇒ интегралы
⇒ интегралы  - ограничены при значениях
- ограничены при значениях  ; аналогично и для интеграла
; аналогично и для интеграла  .
.
По признаку Дирихле эти интегралы сходятся. Покажем, что они сходятся условно.
Так как  , то
, то  "
"  .
.
Далее имеем:  - расходится;
- расходится;
по первому признаку сравнения интеграл  - также расходится; следовательно, расходится и интеграл
- также расходится; следовательно, расходится и интеграл  , где
, где  .
.
Аналогично и для интеграла  . Значит, эти несобственные интегралы сходятся условно.
. Значит, эти несобственные интегралы сходятся условно.
Можно показать, что при 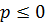 несобственные интегралы:
несобственные интегралы:
 ,
,  - расходятся.
- расходятся.
Таким образом, получаем следующий результат:
| Рис. Условия сходимости несобственных интегралов |
 

|
 условно
при условно
при 
|
 при
при 
|
 абсолютно
при абсолютно
при 
|
§ 5. Несобственные интегралы 2 рода
В этом параграфе рассматриваются функции, заданные на конечном промежутке и не ограниченные на этом промежутке.
Если функция в некоторых точках промежутка не определена, то ее можно в этих точках доопределить какими-нибудь значениями; тем самым функция будет определена уже на всем промежутке. При этом изменение значений функции в нескольких точках, как известно, не меняет значение определенного интеграла и не влияет на интегрируемость функции.
В дальнейшем будет указываться весь промежуток, на котором рассматривается функция; а точки, в которых она не ограничена (или не определена), будут называться особыми точками.
Пусть функция  определена на промежутке
определена на промежутке  и не ограничена на нем. Предположим, что единственной особой точкой на этом промежутке является правый конец промежутка - точка
и не ограничена на нем. Предположим, что единственной особой точкой на этом промежутке является правый конец промежутка - точка  .
.
При этом считаем, что на любом промежутке вида  , где
, где  - достаточно малое положительное число, функция
- достаточно малое положительное число, функция 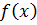 интегрируема.
интегрируема.
|
|
|
Рассмотрим определенный интеграл 
 и поставим вопрос о существовании предела:
и поставим вопрос о существовании предела:

 .
.
Этот предел может быть конечным или бесконечным, а может и вовсе не существовать.
Определение.
Несобственным интегралом  рода от функции
рода от функции 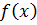 на промежутке
на промежутке  называется выражение
называется выражение  .
.
Это выражение имеет конкретное значение, равное пределу  , если этот предел существует и конечен:
, если этот предел существует и конечен:

 ;
;
в этом случае говорят, что несобственный интеграл  - сходится.
- сходится.
В случае бесконечного предела:  - выражению
- выражению  также приписывают значение
также приписывают значение  ; в этом случае говорят, что несобственный интеграл
; в этом случае говорят, что несобственный интеграл  - расходится:
- расходится:  .
.
Если предел  - не существует, то и в этом случае говорят, что несобственный интеграл
- не существует, то и в этом случае говорят, что несобственный интеграл  - расходится, а выражению
- расходится, а выражению  не приписывают никакого значения.
не приписывают никакого значения.
Аналогично определяется несобственный интеграл  рода в случае, когда единственной особой точкой является левый конец промежутка - точка
рода в случае, когда единственной особой точкой является левый конец промежутка - точка  :
:

 .
.
Пример.
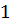 )
) 




 ⇒
⇒
несобственный интеграл сходится и равен  .
.
 )
) 
| Рис. К геометрическому смыслу несобственного интеграла 2 рода |

|

|

|

|

|

|
 ⇒ несобственный интеграл сходится и равен
⇒ несобственный интеграл сходится и равен  .
.
Геометрический смысл
несобственного интеграла  рода.
рода.
Если  на
на  , то
, то
несобственный интеграл 
равен площади бесконечной
(неограниченной сверху) криволинейной
трапеции, ограниченной графиком
функции  , прямыми
, прямыми
 ,
,  и осью абсцисс (см. рис.)
и осью абсцисс (см. рис.)
При этом сходящийся
несобственный интеграл задает
конечную площадь, а расходящийся –
бесконечную площадь.
Если оба конца промежутка  являются особыми точками, то разбиваем этот промежуток на два промежутка произвольной точкой
являются особыми точками, то разбиваем этот промежуток на два промежутка произвольной точкой  :
:

и рассматриваем несобственный интеграл с двумя особыми точками как сумму двух несобственных интегралов с одной особой точкой каждый:

 .
.
Тогда несобственный интеграл  называется сходящимся, если сходятся оба интеграла этой суммы. Если хотя бы одно из этих слагаемых расходится, то несобственный интеграл
называется сходящимся, если сходятся оба интеграла этой суммы. Если хотя бы одно из этих слагаемых расходится, то несобственный интеграл  называется расходящимся.
называется расходящимся.
Пример.
 .
.
Рассмотрим первое слагаемое: 

 ;
;  - расходится ⇒
- расходится ⇒
несобственный интеграл  - также расходится.
- также расходится.
Если имеется единственная особая точка  , которая лежит внутри промежутка
, которая лежит внутри промежутка  , то также разбиваем этот промежуток на два промежутка:
, то также разбиваем этот промежуток на два промежутка:

и рассматриваем несобственный интеграл как сумму двух несобственных интегралов с одной особой точкой  каждый:
каждый:

 .
.
Тогда несобственный интеграл  называется сходящимся, если сходятся оба интеграла этой суммы. Если хотя бы одно из этих слагаемых расходится, то несобственный интеграл
называется сходящимся, если сходятся оба интеграла этой суммы. Если хотя бы одно из этих слагаемых расходится, то несобственный интеграл  называется расходящимся.
называется расходящимся.
Пример.
 .
.
Рассмотрим второе слагаемое:

 ;
;
 - расходится ⇒
- расходится ⇒  - также расходится.
- также расходится.
Пример.
 .
.
Первое слагаемое:

 ∙
∙  .
.
Второе слагаемое:

 ∙
∙  .
.
Оба интеграла сходятся; следовательно, несобственный интеграл
 сходится и равен
сходится и равен  .
.
Если функция 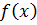 имеет на промежутке
имеет на промежутке  несколько особых точек, то разбиваем промежуток
несколько особых точек, то разбиваем промежуток  на такие частичные промежутки, в каждом из которых есть только одна особая точка; далее рассматриваем несобственный интеграл как сумму несобственных интегралов по каждому из этих промежутков.
на такие частичные промежутки, в каждом из которых есть только одна особая точка; далее рассматриваем несобственный интеграл как сумму несобственных интегралов по каждому из этих промежутков.
В этом случае несобственный интеграл  называется сходящимся, если сходятся все интегралы этой суммы. Если хотя бы одно из этих слагаемых расходится, то несобственный интеграл
называется сходящимся, если сходятся все интегралы этой суммы. Если хотя бы одно из этих слагаемых расходится, то несобственный интеграл  называется расходящимся.
называется расходящимся.
Исследование сходимости несобственного интеграла

 , где
, где  .
.
При  данный несобственный интеграл расходится; действительно:
данный несобственный интеграл расходится; действительно:

 .
.
Пусть  , тогда имеем:
, тогда имеем:

 ∙
∙  .
.
Если 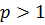 , то
, то  и
и  при
при  ; в этом случае несобственный интеграл
; в этом случае несобственный интеграл  - расходится.
- расходится.
Если  , то
, то  и
и  при
при  ; в этом случае несобственный интеграл сходится и равен:
; в этом случае несобственный интеграл сходится и равен: 
 .
. 
Таким образом, получаем:
Рис. Условие сходимости несобственного интеграла 
|
 
|
 при при 
|
 при при 
|
Геометрический смысл этого результата заключается в следующем.
Площадь бесконечной криволинейной трапеции «под кривой»  на промежутке
на промежутке  является конечной при
является конечной при  и бесконечной при
и бесконечной при 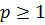 (см. рис.)
(см. рис.)
Рис. Геометрический смысл условия сходимости несобственного интеграла 
|

|

|

|

|

|

|

|

|

|

|

|
Это различие объясняется тем, что графики одних функций «теснее прижимаются» к оси  , чем графики других функций. «Границей» между этими множествами кривых является график функции
, чем графики других функций. «Границей» между этими множествами кривых является график функции  , который ограничивает криволинейную трапецию бесконечной площади.
, который ограничивает криволинейную трапецию бесконечной площади.
Пример.
Найдемплощадь  криволинейной трапеции, ограниченной графиком функции
криволинейной трапеции, ограниченной графиком функции  на промежутке
на промежутке  , где
, где  .
.

 ∙
∙ 
 ∙
∙  ⇒
⇒  (см. рис.)
(см. рис.)
Например:  ,
,  ,
,  .
.
§ 6. Простейшие свойства и вычисление
несобственных интегралов  рода.
рода.
Несобственные интегралы  рода обладают теми же свойствами, что и несобственные интегралы
рода обладают теми же свойствами, что и несобственные интегралы 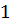 рода. Сформулируем эти свойства, например, для случая, когда единственной особой точкой является правый конец промежутка
рода. Сформулируем эти свойства, например, для случая, когда единственной особой точкой является правый конец промежутка  , т.е. точка
, т.е. точка  .
.
 Аддитивность.
Аддитивность.
Если сходится несобственный интеграл  , то "
, то "  сходится и несобственный интеграл
сходится и несобственный интеграл  , при этом выполняется равенство:
, при этом выполняется равенство:
 .
.
 Линейность.
Линейность.
Если сходятся несобственные интегралы  и
и  , то сходится и несобственный интеграл
, то сходится и несобственный интеграл 
"  ,
,  , при этом справедливо равенство:
, при этом справедливо равенство:

 ∙
∙  ∙
∙  .
.
 Если несобственный интеграл
Если несобственный интеграл  - сходится, то
- сходится, то
 .
.
Методы вычисления несобственных интегралов  рода.
рода.
Вычисление несобственных интегралов  рода основано на тех же формулах, что и вычисление несобственных интегралов
рода основано на тех же формулах, что и вычисление несобственных интегралов 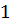 рода.
рода.
Формула Ньютона-Лейбница:
 ,
,
где  - первообразная для функции
- первообразная для функции 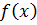 на
на  и
и  .
.
Например:


 .
.
Интегрирование по частям:  .
.
Пример.


 ∙
∙ 


 .
.
Замена переменной:  .
.
Пример.




 .
.
§ 7. Признаки сходимости несобственных интегралов 2 рода
В случае, когда вычисление несобственного интеграла  рода
рода  невозможно или затруднительно, для решения вопроса о существовании (сходимости) этого несобственного интеграла применяются признаки сходимости.
невозможно или затруднительно, для решения вопроса о существовании (сходимости) этого несобственного интеграла применяются признаки сходимости.
Признаки сходимости для несобственных интегралов  рода аналогичны признакам сходимости несобственных интегралов
рода аналогичны признакам сходимости несобственных интегралов 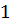 рода.
рода.
Для определенности будем рассматривать несобственные интегралы
 рода
рода  , где точка
, где точка  является единственной особой точкой промежутка
является единственной особой точкой промежутка  . Признаки сходимости, которые будут установлены для них, переносятся и на другие типы несобственных интегралов
. Признаки сходимости, которые будут установлены для них, переносятся и на другие типы несобственных интегралов  рода.
рода.
Признаки сходимости для положительных функций.
Пусть  "
"  (или, по крайней мере "
(или, по крайней мере "  , где
, где  - достаточно малое положительное число).
- достаточно малое положительное число).
Сходимость несобственного интеграла  от положительной функции
от положительной функции  равносильна ограниченности соответствующих определенных интегралов:
равносильна ограниченности соответствующих определенных интегралов:
 - сходится ⇔
- сходится ⇔  :
:  "
"  .
.
Признаки сравнения.
Рассмотрим несобственные интегралы  рода от положительных функций:
рода от положительных функций:
 ,
, 
 , где
, где  ,
,  "
"  .
.
Теорема 1 (первый признак сравнения).
Пусть  "
"  . Тогда
. Тогда
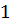 ) из сходимости
) из сходимости  следует сходимость
следует сходимость  и справедлива оценка:
и справедлива оценка:  ;
;
 ) из расходимости
) из расходимости  следует расходимость
следует расходимость  .
.
Пример.
Исследуем сходимость несобственного интеграла  .
.
Здесь  - положительная функция на
- положительная функция на  ,
,
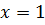 - особая точка,
- особая точка,  "
"  ;
;
несобственный интеграл  – сходится (см. Пример выше).
– сходится (см. Пример выше).
По первому признаку сравнения интеграл  - также сходится.
- также сходится.
Теорема 2 (второй признак сравнения).
Пусть  ,
,  "
"  и существует предел
и существует предел
 .
.
Тогда оба интеграла  и
и  - сходятся или оба интеграла расходятся, т.е. если один из них сходится, то и другой сходится, а если один из них расходится, то и другой расходится.
- сходятся или оба интеграла расходятся, т.е. если один из них сходится, то и другой сходится, а если один из них расходится, то и другой расходится.
Пример.
Исследуем сходимость несобственного интеграла  .
.
Здесь  - положительная функция на
- положительная функция на  ,
,
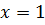 - особая точка;
- особая точка; 

 ∙
∙ 
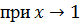 .
.
Применим второй признак сравнения; для этого в качестве функции  можно взять функцию
можно взять функцию 
 , т.к.
, т.к.  .
.
Тогда имеем: 
 ∙
∙  ⇒
⇒  - сходится;
- сходится;
по второму признаку сравнения  - также сходится.
- также сходится.
Признаки сходимости для произвольных функций.
Рассмотрим несобственные интегралы  рода
рода  , где функция
, где функция 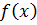 является знакопеременной при
является знакопеременной при
 2020-10-10
2020-10-10 2557
2557