2020-10-09
3187
Основной характеристикой множеств является количество элементов, содержащихся в этом множестве.
По данному признаку выделяются:
1. Множество, содержащее конечное число элементов называется конечным.
Количество элементов конечного множества называют его мощностью.
2. Множество, не являющееся конечным, называется бесконечным.
3. Если множество не содержит элементов, то оно называется пустым и обозначается 
.
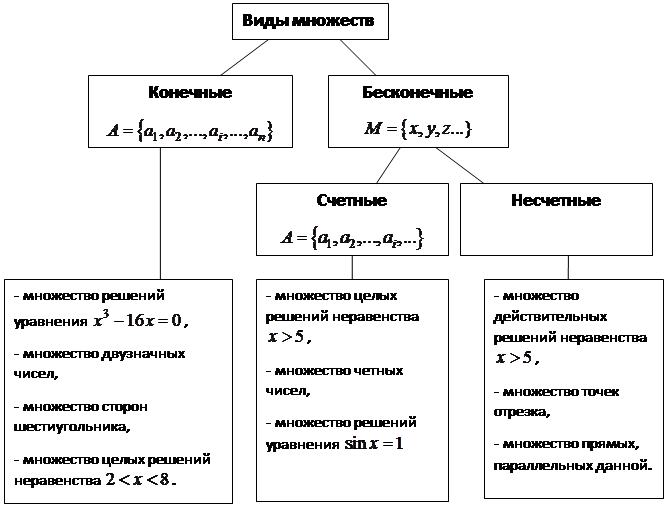
1. Конечное множество по признаку мощности характеризуется:
Два множества А и В называются эквивалентными, или, равномощными, если между их элементами можно установить взаимно-однозначное соответствие.
Пример: Рассмотрим множества, состоящие из букв слов:
; 
; 
; 
.
Множества А, В и С имеют равные мощности: 
, а мощность множества D меньше 
.
При этом, множества А и В равны, а множества А и С – эквивалентны.
Эталоном для сравнения множеств служит натуральный ряд чисел. Поэтому все числовые последовательности, содержащие различные элементы, эквивалентны натуральному ряду чисел, что видно по их индексам.
|
|
|
2. Бесконечное множество, которое эквивалентно множеству натуральных чисел, называется счетным.
Говорим, что все элементы счетного множества пронумерованы.
В противном случае бесконечное множество будет несчетным.
В 1878 году Георг Кантор доказал, что множество точек, расположенных на отрезке от 0 до 1 несчетно.
Во множестве могут быть выделены подмножества.
Если каждый элемент множества K принадлежит множеству М, то множество К называют подмножеством множества М и обозначают 
.
Например:
1) множество всех книг данного автора в библиотеке, есть подмножество всех книг в библиотеке.
2) множество студентов, обучающихся на "4" и "5" в группе есть подмножество всех студентов группы.
3) 
четных чисел меньших или равных 6, есть подмножество множества 
.
Пустое множество является подмножеством любого множества.
Количество подмножеств для исходного множества может быть рассчитано.
Для этого познакомимся с термином булеан.
Булеаном множества М (N(M)) называется множество всех его подмножеств.
Пример:
Рассмотрим множество 
. Составим все подмножества множества М.
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
, 
.
Подмножества и 
являются несобственными подмножествами множества М,
остальные – 2-15 – это собственные подмножества.
Всего мы нашли 16 различных подмножеств множества М. Это число 16 может выразить: 
.
В общем случае, для любого конечног о множества, состоящего из n элементов, число возможных подмножеств равно 
.
Множество U, состоящее из всех возможных элементов, обладающих данным признаком, называется универсальным.
Вопрос 2. Операции над множествами
|
|
|
И свойства операций
Множества изображаются при помощи диаграмм Эйлера-Венна (круги на плоскости).
Элементы множества изображаются точками:
- внутри круга, если они принадлежат данному множеству;
- вне круга, если не принадлежат.
, 
.
Основными операциями над множествами являются операции:
- пересечение,
- объединение,
- разность,
- симметрическая разность,
- дополнение.
1. Пересечением множеств А и В называется множество 
, состоящее из элементов, которые принадлежат одновременно как множеству А так и множеству В.
Пример: Если 
, 
, то 
.
При помощи диаграмм Эйлера-Венна пересечение множеств изображается следующим образом:
2. Объединением множеств А и В называется множество 
, состоящее из элементов, которые принадлежат или множеству А или множеству В.
Пример: Если 
, 
, то 
.
При помощи диаграмм Эйлера-Венна объединение множеств изображается следующим образом:
3. Разностью множеств А и В называется множество 
, состоящее из элементов множества А, которые не принадлежат множеству В.
Пример: Если 
, 
, то 
.
Р азность множеств изображается следующим образом:
По диаграмме видно, что 
можно заменить на 
.
4. Симметрической разностью А и В называется множество 
, состоящее из элементов множеств А или В, но не принадлежащих этим множествам одновременно.
Пример: Если 
, 
, то 
.
При помощи диаграмм Эйлера-Венна симметрическая разность множеств изображается следующим образом:
5. Дополнением множества А до множества U называется множество 
, состоящее из элементов множества U, которые не принадлежат множеству А.
При помощи диаграмм Эйлера-Венна дополнение множества изображается следующим образом:
Свойства операций
Операции над множествами обладают рядом свойств, похожих на свойства операций сложения и умножения чисел.
| Объединение (сложение) | Пересечение (умножение) |
| 1. Коммутативность (переместительное свойство) | |
 |  |
| 2. Ассоциативность (сочетательное свойство) | |
 |  |
| 5. Дистрибутивность пересечения относительно объединения | |
|
| |
| 6. Дистрибутивность объединения относительно пересечения | |
|
| |
| 5. Закон поглощения | |
 |  |
| 6. Закон де Моргана | |
 |  |
| 7. Закон склеивания | |
 |  |
| 8.Ззакон Порецкого | |
 |  |
 ,  |  ,  |
 ,  |  ,  |
Используя эти операции можно выражать одни множества через другие, при этом сначала выполняется операция дополнения, затем пересечения и только затем операции объединения и разности. Для изменения порядка в выражении используют скобки.
Пример. Доказать справедливость следующего равенства и проверить результат на диаграмме Эйлера-Венна: 
.
Решение. Преобразуем по очереди левую и правую части данного равенства:
1) 
. Заменили разность на пересечение с дополнением.
2) 
.
Использовали переход от разности к пересечению, закон де Моргана, свойство дистрибутивности, свойство 
и 
.
После преобразования видно, что левая и правая части равенств одинаковые, следовательно, равенство доказано.
Проверим равенство на диаграмме Эйлера-Венна.
