Лекция 2. Формы представления высказываний
План лекции:
Дизъюнктивные и конъюнктивные нормальные формы ДНФ, КНФ.
Совершенные нормальные формы СДНФ, СКНФ
Дизъюнктивные и конъюнктивные нормальные формы ДНФ, КНФ
Нормальная форма – это синтаксически однозначный способ записи формулы, реализующей данную функцию.
Любая n -членная операция, обозначаемая, например, 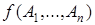 , будет полностью определена, если установлено, при каких значениях высказываний
, будет полностью определена, если установлено, при каких значениях высказываний 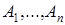 результат будет истинным или ложным. Один из способов задания такой операции – заполнение таблицы значений:
результат будет истинным или ложным. Один из способов задания такой операции – заполнение таблицы значений:
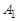 | 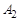 | 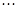 | 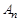 | 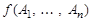 |
| 1 | 1 | 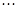 | 1 | 1 или 0 |
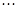 | 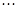 | 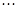 | 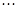 | 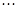 |
| 0 | 0 | 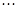 | 0 | 1 или 0 |
В таблице значений высказывания, образованного от n простейших высказываний 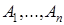 , имеется
, имеется 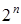 строк. Столбец значений имеет также
строк. Столбец значений имеет также 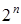 позиций. Следовательно, имеется
позиций. Следовательно, имеется 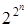 различных вариантов его заполнения, и, соответственно, число всех n -членных операций равно
различных вариантов его заполнения, и, соответственно, число всех n -членных операций равно 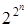 . При n=1 число одночленных операций равно 4, при n=2 число двучленных – 16, при n=3 количество трехчленных – 256 и т.д.
. При n=1 число одночленных операций равно 4, при n=2 число двучленных – 16, при n=3 количество трехчленных – 256 и т.д.
Рассмотрим некоторые специальные виды формул.
Формулу называют элементарной конъюнкцией, если она является конъюнкцией переменных и отрицаний переменных. Например, формулы 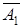 ,
, 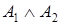 ,
, 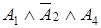 ,
, 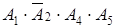 – элементарные конъюнкции.
– элементарные конъюнкции.
Формулу, представляющую собой дизъюнкцию (возможно одночленную) элементарных конъюнкций, называют дизъюнктивной нормальной формой (д. н. ф.). Например, формулы 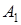 ,
, 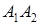 ,
, 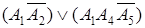 .
.
Теорема 2.1. (о приведении к ДНФ). Для любой формулы U можно найти равносильную ей формулу V, являющуюся ДНФ.
Формулу называют элементарной дизъюнкцией, если она является дизъюнкцией переменных и отрицаний переменных. Например, формулы 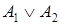 ,
, 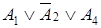 ,
, 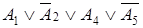 и т.д.
и т.д.
Пример. 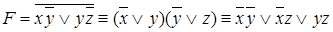
Такая форма называется дизъюнктивной нормальной формой (ДНФ). Отдельный элемент ДНФ называется элементарной конъюнкцией или конституентой единицы.
Формулу, являющуюся конъюнкцией (возможно одночленной) элементарных дизъюнкций, называют конъюнктивной нормальной формой (КНФ). Например, формулы 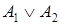 ,
, 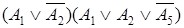 .
.
Теорема 2.2. (о приведении к КНФ). Для любой формулы U можно найти равносильную ей формулу V, являющуюся КНФ.
Пример. 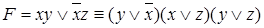
Отдельный элемент КНФ называется элементарной дизъюнкцией или конституентой нуля.
Алгоритм построения КНФ и ДНФ.
1) Избавиться от всех логических операций, содержащихся в формуле, заменив их основными: конъюнкцией, дизъюнкцией, отрицанием. Это можно сделать, используя равносильные формулы (см. Лекцию 1).
2) Заменить знак отрицания, относящийся ко всему выражению, знаками отрицания, относящимися к отдельным переменным высказываниям на основании закона де Моргана.
3) Избавиться от знаков двойного отрицания.
4) Применить, если нужно, к операциям конъюнкции и дизъюнкции свойства дистрибутивности и формулы поглощения.
Примеры.
1. Приведем к КНФ формулу 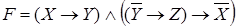
Преобразуем формулу F к формуле, не содержащей импликацию:
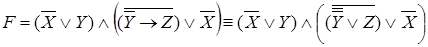
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
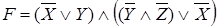
По закону дистрибутивности получим КНФ:
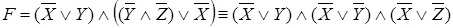
2. Приведем к ДНФ формулу:
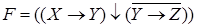 .
.
Выразим логические операции импликации и стрелку Пирса через конъюнкцию, дизъюнкцию и инверсию:
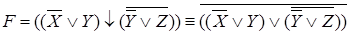
В полученной формуле перенесем отрицание к переменным и сократим двойные отрицания:
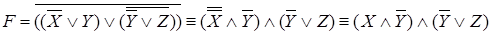
Используя закон дистрибутивности, приводим формулу к ДНФ:
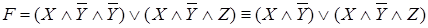
 2020-10-10
2020-10-10 3887
3887