Предел функции в точке и бесконечности

С понятием предела числовой последовательности 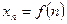тесно связано понятие предела функции 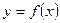в бесконечности. Здесь аргумент х, изменяясь, может принимать различные значения.

Определение. Число А называется пределом функции y= f(x) при х, стремящимся к бесконечности, если для любого, сколь угодно малого положительного числа 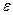, найдется такое положительное число М>0 (зависящее от 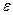, т.е. М=М(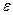)), что при 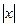>M верно неравенство <.

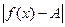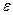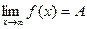В этом случае записывают:

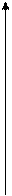у

А+ε

А

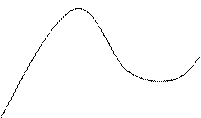
А-ε

0 М х

Рис.5.2.1

С помощью логических символов определение можно записать следующим

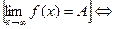
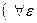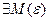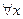образом: >0) () (> M) <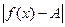

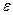
Геометрически это же определение означает: как только 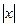>M график функции лежит внутри полосы шириной 2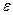, т.е. 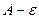< f(x)<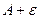, какой бы узкой ни была эта полоса (рис.5.2.1)

Пример. Доказать, что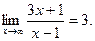

Пусть 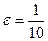. Найдем такое М>0, чтобы <<

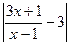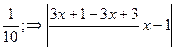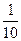
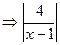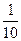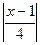<, >10 х>41; М=41. если х >41 выполняется условие 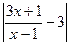<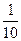.Значит,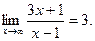

Замечание. Приведенное определение предела функции подразумевает под высказыванием 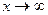, что 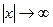. Но т.к. возможны случа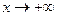и или 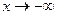, то для 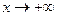определение совпадает с приведенным, а если 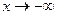, то ищется такое М, чтобы выполнялось условие x <-M.

Пусть функция 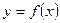определена в некоторой окрестности точки а (кроме, может, самой точки а).

Определение. Число А называется пределом функции 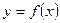при х, стремящимся к а (или в точке а), если для любого, сколь угодно малого положительного числа ε найдется такое положительное 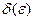, что для всех х не равных а и удовлетворяющих условию x – a δ выполняется условие 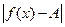< ε

В этом случае записывают: 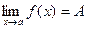. (5.2.1)

С помощью логических символов равенства (5.1) (или определение предела

функции) запишется:

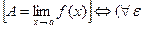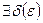>0) (>0) (<) <.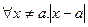

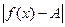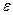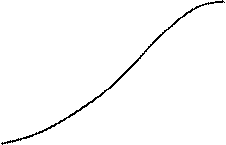
Рассмотрим геометрический смысл предела функции.

y

А+ε

А 2ε

А-ε

0 а-δ а х а+δ х

Рис.5.2.2

< <<

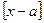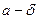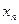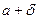
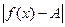<ε 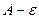< f(x) < A+ε (5.2.2)

Совместное выполнение неравенств (5.2.2) означает:

Число А является пределом функции 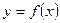при x → a, если для любой 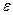-окрестности точки А найдется такая - окрестность точки а, соответствующие значения функции f(x) лежат 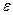-окрестности точки А, т.е. внутри полосы 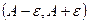(шириной 2).

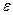Замечание. Т.к. предел рассматривается при значениях 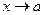(но 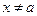), то поведение функции в самой точке а в данном случае не представляет интереса.