Микропроцессоры типа CISC

КЛАССИФИКАЦИЯ И РОДОСЛОВНАЯ ПОНЯТИЙ.

ОШИБКИ В ОПРЕДЕЛЕНИЯХ. КОНТПРИМЕРЫ.

УСВОЕНИЕ МАТЕМАТИЧЕСКИХ ПОНЯТИЙ

ОПРЕДЕЛЕНИЕ ПОНЯТИЯ.

РОДОВИДОВЫЕ И ДРУГИЕ ОТНОШЕНИЯ ПОНЯТИЙ.

ПОНЯТИЕ, ЕГО СОДЕРЖАНИЕ И ОБЪЕМ.

Понятие – форма научного познания, отражающая существенное в изучаемых объектах и закрепляемая специальными терминами. В математике понятие обозначается не только термином (слово или группа слов), но и символом – знаком.

Признаком называют все то, в чем объекты сходны друг с другом или в чем они отличаются. Существенные признаки необходимо принадлежат элементам данного множества и отличают их от элементов других множеств. Несущественные признаки не дают возможности познать эти элементы, отличить их от элементов других множеств. В понятии находят отражение лишь существенные в каком-либо отношении его признаки, называемые признаками понятия. С помощью анализа выделяют признаки объектов, а с помощью синтеза соединяют существенные признаки, отвлекаясь от остальных, несущественных, в единое целое – понятие. Кроме абстрагирования здесь имеет место еще процесс обобщения, когда в рассматриваемом множестве предметов находят признаки, присущие всем элементам данного множества.

Каждое понятие имеет свои существенные признаки, составляющие содержание понятия. Множество всех тех и только тех объектов, которые обладают этими признаками, составляют объем понятия. Между содержанием и объемом понятия существует обратно пропорциональная зависимость, а, именно, чем шире объем понятия, тем беднее его содержание и наоборот. Например, объем понятия «ромб» шире, чем объем понятия квадрат, зато содержание первого, (все стороны равны) меньше чем содержание второго (все стороны равны и углы прямые).

Если объем понятия состоит из одного предмета, то оно называется единичным. Примерами единичных понятий являются пустое множество, трехмерное евклидово пространство, производная функции 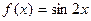в точке х =1 и т.д. Если объем понятия включает в себя более одного предмета, а признаки понятия являются общими для всех этих предметов, то понятие называется общим. Например, такие понятия как, точка, уравнение, задача – общие понятия. Единичные понятия не следует путать с конкретными (отражающими конкретные вещи) и общие с абстрактными (взятые как самостоятельный объект мысли). Например, модель куба – понятие общее и конкретное, а куб – понятие общее и абстрактное.

Между понятиями существуют отношения, отражающие связи соответствующих понятиям множеств объектов. Важнейшей формой связи понятий является их родовидовое подчинение, которое складывается при формировании понятий и обнаруживается там и тогда, где и когда имеет место непосредственная преемственность в переходах от одних понятий к другим. Например, объединение понятий «сложение», «вычитание», «умножение», «деление» приводит к понятию «арифметическая операция». Оно будет подчинять четыре предыдущих понятия как видовые и станет для них родовым. На базе понятий (видовых) «арифметические операции», «возведение в степень» и «извлечение корня» образуется новое (родовое) понятие «алгебраическая операция», с которыми связаны такие понятия, как «алгебраическое выражение», «алгебраическое уравнение» и др.

Символизируя понятия в виде кругов Эйлера, каждое родовидовое отношение понятий изображается двумя кругами (рис.1), из которых один (В – вид) содержится внутри другого (Р – род).

В родовидовых отношениях следует различать ближайший род и последующие родовые ступени. Так для вида В₁ ближайшим родом будет род Р₁, а не Р₂. Род Р₂ будет ближайшим для вида В₂, а не для В₁ (рис.1). В₁, Р₁=В₂ и Р₂ можно проиллюстрировать, например, такими понятиями: пусть В₁ – «целое число», Р₁=В₂ – «рациональное число», Р₂ – «действительное число». С помощью знаков включения это можно представить так: В₁ÌР₁, В₂ÌР₂.

Не всегда легко и однозначно можно определить ближайший род. Если между зависимыми понятиями нельзя поставить еще одно понятие, будем иметь отношение ближайшего рода и вида. Так между понятиями «прямоугольник» (ПК) и «четырехугольник» (ЧК) можно поставить понятие «параллелограмм» (ПМ), поэтому ближайшим родом для понятия ПК является понятие ПМ, хотя прямоугольник – такой же четырехугольник, как и параллелограмм.

Рис.1.

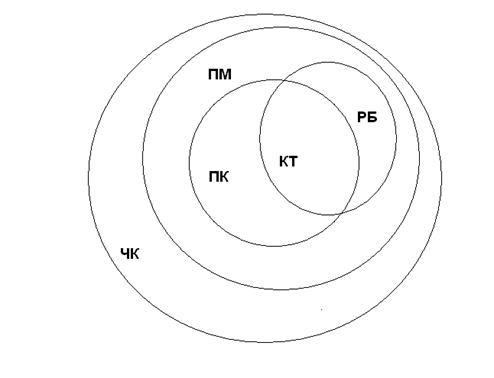
Рис.2

Для понятия «квадрат» (КТ) имеется несколько ближайших понятий: «прямоугольник» (ПК) и «ромб» (РБ), а ПМ не является ближайшим понятием (рис.2). Если символами КТ, ПК,и РБ обозначить соответствующие множества фигур (объемы понятий), то с помощью символа пересечения множеств запишем

КТ=ПКÇРБ,

т.е. все квадраты являются одновременно и прямоугольниками и ромбами. Последовательная подчиненность понятий отражается в следующих записях:

КТÌПКÌПМÌЧК, КТÌРБÌПМÌЧК.

Перемещение по ступенькам лестницы родовидовых отношений понятий в направлении от вида к роду ведет к расширению, обобщению понятий, а обратный переход – к их ограничению.

Существуют и другие отношения понятий, которые дают возможность характеризовать понятия как сравнимые, когда у них есть общие признаки (например, треугольник и квадрат), и несравнимые, когда таких признаков нет (например, треугольник и процент). Сравнимые понятия могут быть совместимыми и несовместимыми в зависимости от того, совпадают их объемы (полностью или частично) или не совпадают. Совместимые понятия могут быть равнозначащими (совпадающими, например полупрямая и луч), перекрещивающимися (пересекающимися, например целое число и положительное число) подчиненными и подчиняющими (квадрат числа и степень числа), соподчиненными (ромб и прямоугольник по отношению к параллелограмму). Несовместимые понятия могут быть противоположными (например, равносторонний и неравнобедренный треугольники), противоречащими (например, равнобедренный и неравнобедренный треугольники) соподчиненными (например, логарифмическое и тригонометрическое уравнения по отношению к трансцендентному уравнению).

Определение понятия (или дефиниция, сокращено Df) есть раскрытие содержания этого понятия, перечисление его существенных, отличительных признаков с помощью которых выделяются все обладающие этими признаками объекты, и только такие объекты и объединяются в единое целое с помощью данного понятия.

Понятия находятся в родовидовом отношении, и наиболее удобный общий способ определения понятия – определение через ближайший род и видовое отличие. К отысканию ближайшего рода следует стремиться потому, что в таком случае мы подходим ближе к определяемому понятию, его объему и благодаря этому уменьшается совокупность видовых признаков в определении. Например, для квадрата ближайшими родовыми понятиями будут «прямоугольник» и «ромб» и в каждом случае определение содержит по одному видовому признаку квадрата: «Квадрат есть прямоугольник, у которого все стороны равны»; «Квадратом называется ромб, у которого все углы прямые». Если же взять не ближайший род – параллелограмм, то видовых признаков квадрата будет два: «Квадратом называется параллелограмм, у которого все стороны равны и все углы прямые».

Определение через ближайший род и видовое отличие является самым распространенным в математике. Однако наряду с ним используются и другие разновидности определений, многие из которых можно свести к родовидовой форме определения.

Генетическое определение показывает, как возникает, образуется данный предмет или явление. Например: «Линейным углом двугранного угла называется плоский угол, получающийся в пересечении двугранного угла плоскостью, перпендикулярной ребру этого двугранного угла». В генетическом определении часто заложен также способ построения этого объекта. Например в определении линейного угла содержится алгоритм его построения: нужно выбрать точку на ребре двугранного угла и в этой точке восстановить лучи, перпендикулярные ребру в каждой из граней двугранного угла. Генетическое определение можно дать также окружности, кругу, сфере, шару, цилиндру, конусу и ряду других понятий.

Существуют рекуррентные или индуктивные определения (арифметическая и геометрическая прогрессии), когда указывается способ получения нового, кроме первого, члена через предыдущий. Аналогичным образом задаются и возвратные последовательности второго рада, когда каждый следующий член последовательности, кроме первых двух, задается с помощью двух предыдущих. Например: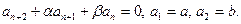

Встречаются иногда определения, раскрывающие значение термина путем такого перечисления объектов, которое создает представление об объеме и содержании понятия. Например: «Натуральный ряд чисел – это 1,2,3, и т.д.».

В математике некоторые определения удобно выражать символическим языком в виде равенств:

1) ;

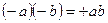2) ;

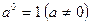3);

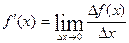4) .

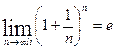Существуют логические формы, которые не являются определениями, но близки к определению, иногда заменяют или дополняют его. Приведем примеры.

Описание понятия обычно применяется в тех случаях, если невозможно или нецелесообразно вводить определение. Таким образом вводятся первичные понятия – число, точка, прямая плоскость, множество и др.В определении определяемое понятие вводится через уже известное понятие, но самое первое понятие каждой науки еще не к чему сводить, поэтому ввести его через определение невозможно.

Описательно приходится вводить несколько первичных понятий, Иногда заменяют описанием логически возможное, но слишком сложное, громоздкое и неудобное понятие. Иногда описание понятия может не только заменить его определение, но и дополнять ее такой информацией, которая конкретизирует понятие, расширяет связи с другими понятиями, полнее раскрывает его содержание, помогает учащимся глубже понять и прочнее усвоить новое понятие. Особенно часто этот прием введения новых понятий используется в младших и средних классах, когда определению понятия предшествует его описание, рассмотрение различных примеров и задач где используется это понятие.

В средней школе встречается еще так называемое косвенное определение понятия с помощью аксиом. Так в геометрии аксиомы раскрывают свойства и отношения первичных понятий «точка», «прямая» и др. В математике применяется аксиоматическое определение, которое дается с помощью совокупности аксиом, включаемых в определение понятия без дополнительного описания его. Например, определения натуральных чисел с помощью системы аксиом Пеано, понятие группы, поля, кольца и др.

Отметим еще правила построения определения:

1) оно должно быть полным и точным, четким и ясным;

2) нельзя определять понятие через неизвестное понятие или неизвестный признак;

3) нельзя допускать логического круга: А определять через В, а В – через А;

4) избегать отрицательных определений, т.е. указаний на то, чем определяемый объект не обладает (например, определение «нечетная функция есть функция не являющаяся четной» не будет верным определением, поскольку существуют функции которые не являются ни четными, ни нечетными).

Каждое понятие должно быть правильно понято, сознательно и четко усвоено всеми учащимися еще на уроке. Эта цель должна достигаться уже в процессе введения понятия, но понятие должно закрепляться на данном и повторяться на последующих уроках путем воспроизведения учащимися определения (или описания), приведения иллюстрирующих и конкретизирующих его примеров, проведения логического анализа определения и другой творческой работы, использования понятия в суждениях и умозаключениях. Контроль за усвоением понятия осуществляется обычно в виде опроса учащихся, при котором нужно, как правило, требовать подтверждение определения примерами, причем не только готовыми, взятыми из учебника, но и придуманными самостоятельно. Это требование должно стать правилом, причем ученики должны знать о нем, и дома, готовясь к занятиям, подыскивать свои примеры.

Вторым хорошим приемом при усвоении и запоминании определения понятия, является работа с самим определением, когда требуется среди несколько приведенных определений выбрать правильное и объяснить почему остальные определения являются неверными или неточными. Следует также проводить работу (особенно среди слабых учеников) требующую в текст определения вставить одно или несколько слов, словосочетаний. Все это приводит к неформальной работе над понятием и способствует активному запоминанию определений.

Эта творческая мыслительная работа развивает мышление школьников и способствует сознательному, глубокому и прочному усвоению сущности, содержания и объема понятия, исключает его формальное изучение, механическое заучивание определения. Формальное, поверхностное усвоение понятий ведет к их смешению, неточному пониманию и неправильному использованию, а в конечном счете – к формальному прохождению всего курса, плохому, поверхностному его усвоению. Другие понятия, введенные через недостаточные осмысленные понятия, будут еще более туманными, и правильное самостоятельное использование их в умозаключениях становится для некоторых учащихся невозможным. Такие понятия не могут «работать», и в результате не будет работать вся совокупность формальных математических знаний, обреченная на скорое забывание. Умственное развитие от такого обучения также незначительно.

Каждый ученик должен знать определения изученных понятий, однако требовать заучивания формулировок понятий без их осознания не стоит, так как это может привести к формализму. Надо ориентировать школьников на смысловое, логическое запоминание, которое должно стать результатом осмысливания определения, его структуры в процессе изучения и применения. Выделение родового понятия и видовых признаков, подыскание нескольких своих по возможности разнообразных примеров и проверка их на предмет полного удовлетворения всем требованиям определения – эффективное средство достижения сознательного усвоения понятия и его определения. Необходимо постепенно раскрывать перед учащимися общую логическую структуру определения, учить самостоятельно конструировать его для новых понятий.

Ученики должны знать, что дословное соблюдение формулировки, данной в учебнике, весьма желательно, хотя от ее формы можно отступить, передать частично «своими словами», но все содержание книжной формулировки обязательно сохранить точно. Когда ученик формулирует определение «своими словами», здесь скорее всего возможны ошибки, которые помогают выявить значение некоторых необходимых элементов определения и пробелы в усвоении понятия, с тем чтобы неотложно устранить их. Заученная формулировка может скрывать подобные пробелы. Учитель должен учить школьников выражать мысли «своими словами», поощрять их к этому, терпеливо подводить к самостоятельному исправлению ошибки. При дословных книжных формулировках особенно необходимо проверять сознательность их усвоения учащимися. На примерах таких формулировок, в которых нельзя пропустить ни одного слова, учитель прививает ученикам вкус к высокой логической культуре мышления и речи, учит их выражаться лаконично и точно.

Нельзя допускать поспешности при введении новых понятий, особенно если они сложны, трудны для учащихся и обладают высокой степенью абстракции (например, «функция», «предел», «производная», «интеграл» и др.). Практика показывает, что время, дополнительно затраченное при введении нового понятия на всестороннее, глубокое его изучение и сознательное усвоение, окупается в дальнейшем благодаря более легкому и результативному усвоению последующих связанных с этим понятием вопросов. И наоборот, результатом чрезмерной поспешности при изучении нового сложного понятия являются дальнейшие затруднения и не всегда восполнимые потери в достигаемом уровне знаний. В этом и заключается одна из причин того, что одна и та же тема или раздел учебного материала у одних учителей считается трудным для учащихся, а у других никаких затруднений не вызывает.

Например, при введении достаточно сложного понятия «призма», можно поступить следующим образом.

Вначале разбирается наглядный пример какой-то призмы, хотя до этого школьники уже не раз сталкивались с этим многогранником при решении задач, отмечаются ее наиболее характерные свойства: равенство и параллельность оснований, равенство и параллельность боковых ребер и др. Затем вводится точное определение понятия призмы.

Призмой называется многогранник, у которого две грани – n-угольники, а все остальные n граней – параллелограммы.

После этого следует еще поработать с этим определением, предлагая учащимся найти ошибки в следующих «определениях».

1) Призмой называется многогранник, у которого две грани – равные многоугольники с соответственно параллельными сторонами, а все остальные грани – параллелограммы.

2) Призмой называется многогранник, у которого две грани – равные n-угольники с соответственно параллельными сторонами, а все остальные n граней – параллелограммы.

3) Призмой называется многогранник, у которого две грани –n-угольники лежащие в параллельных плоскостях, а остальные n граней – параллелограммы.

4) Призмой называется многогранник, у которого две грани – плоские n-угольники, а все остальные n граней – параллелограммы.

Такая неформальная работа с определением призмы позволит школьникам яснее осознать это понятие и лучше его усвоить.

При всех видах повторения продолжается работа по дальнейшему усвоению математических понятий. Главное внимание при этом уделяется не воспроизведению определений, а различным видам творческой работы учащихся с понятиями, их применениями при решении разного рода задач, различным видам связей и отношений между понятиями.

Отметим некоторые ошибки, допускаемые учащимися в определениях.

Иногда учащиеся допускают «порочный круг» в определении. Например, прямой угол определяют как угол со взаимно перпендикулярными сторонами, а взаимно перпендикулярные прямые – через понятие прямого угла. Но определить прямой угол через понятие перпендикулярности прямых имеем право лишь в том случае, если перпендикулярность прямых была уже определена ранее, причем не через понятие прямого угла, а через другое известное понятие.

Другим примером «порочного круга» может служить определение иррациональных чисел через вещественные («вещественные, не являющиеся рациональными») и вещественных через иррациональные («числа рациональные и иррациональные называются вещественными»). Иногда ученики действие сложения определяют через сумму, а сумму через сложение. Чтобы избежать таких логических ошибок, учащимся следует разъяснять необходимость придерживаться определенной последовательности введения понятий, принятой в том учебнике, по которому изучается курс математики в данном классе.

Недопустима в определениях тавтология, когда объект определяют через самого себя, хотя и в других выражениях, например: «Делением называется действие, при котором одно число делят на другое»; «Многоугольники называются подобными, если они подобны между собой» и т.п.

Логически несовершенное определение получают тогда, когда в него включают логически зависимые друг от друга свойства. Например, в одном из школьных учебников содержалось такое определение: «Треугольники называются подобными, если 1) углы одного соответственно равны углам другого; 2) стороны одного пропорциональны сходственным сторонам другого». Каждое из этих двух свойств может служить признаком определяемого понятия, а другое можно выбросить из определения и доказать как теорему (это фактически есть первый и третий признаки подобия треугольников).

Иногда учащиеся дают такое определение: «Параллелограммом называется такой четырехугольник, у которого противоположные стороны попарно равны и параллельны», т.е. включают свойство равенства противоположных сторон, которое является логическим следствием признака понятия (попарной параллельности противоположных сторон) и составляет содержание следствия из теоремы. Хотя включение в определение логически зависимых друг от друга свойств и не ведет к фактическому изменению содержания и объема понятия, однако оно является свидетельством невысокого логического уровня математических знаний ученика. В такой ситуации следует предложить ученику привести пример такого параллелограмма, в котором противоположные стороны были бы попарно параллельны, но не равны. Такой фигуры ученик не придумает, а соответствующая теорема подскажет, что ее и быть не может. Следовательно, нет основания включать в определение параллелограмма требование равенства противоположных сторон, ибо оно и без того выполняется.

В определении параллелограмма встречаются ошибки, изменяющие содержание понятия и искажающие сущность определения: «Параллелограммом называется четырехугольник с параллельными сторонами» (или: «у которого имеются параллельные стороны»). Выражение «с параллельными сторонами» неопределенно: все четыре стороны четырехугольника параллельными между собой быть не могут, поэтому оно означает параллельность двух сторон, т.е. признаки вида указаны не полностью, содержание понятия сузилось, а объем его расширился (охватывает параллелограммы и трапеции). Это результат пропуска в определении только одного слова («попарно»). Здесь как правило, необходимо привести ученика к исправлению своей ошибки, что можно сделать, например, так: «Нарисуйте параллелограмм АВСД; сколько параллельных сторон? (четыре); следовательно АВ÷÷АД? (нет, не параллельны); можно здесь говорить о четырех параллельных сторонах? (нельзя); значит в вашем определении говорилось только о двух параллельных сторонах и вот такую фигуру (учитель рисует трапецию) придется называть параллелограммом». Полученное противоречие отвергает определение, данное учеником, и в этом заключается один из основных методов опровержения ошибочных суждений и определений – приведение к противоречию.

Другим аналогичным средством являются контрпримеры. Например, к определению, данному учеником: «Квадратным уравнением называется такое уравнение, которое содержит переменную во второй степени» учитель предлагает контрпример: 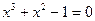, из которого выясняется, что квадратное уравнение не должно содержать более высоких степеней переменной, чем 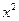. Затем учитель последовательно предлагает следующие контрпримеры: 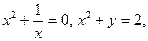из которых выясняются два других упущенных в определении признака понятия «квадратное уравнение».

Часто ученики дают следующее определение: «Угол, больший прямого, называется тупым» (по аналогии с определением острого угла). В качестве контрпримера учитель предлагает угол в 300^о, с помощью которого выясняется, случайно ли упущено ограничение «меньше 2d».

Для устранения ошибки в определении «Два уравнения равносильны, если все корни одного являются корнями второго» можно использовать такой контрпример: 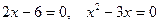. После уточнения «и наоборот», нужно рассмотреть такой пример: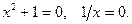

Учащиеся допускают ошибки в использовании родового понятия, когда они либо совсем опускают это понятие и заменяют его другими словами, либо берут не ближайший род. Например, медиану определяют не через понятие отрезок, а как «прямую, соединяющую вершину треугольника с серединой противоположной стороны». Но медиана отрезок, а не прямая.

Требуя от учащихся содержательной точности определений, учитель добивается точности в усвоении математических понятий, знаний и оттачивает логическое мышление. Как правило, ошибки следует разбирать, привлекая всех учащихся к их выявлению и устранению, пользуясь при этом контрпримерами или приведением к противоречию.

Классификацией понятия называется деление (разбиение) объема этого понятия на подмножества (классы), удовлетворяющие следующим требованиям:

1) деление производится по одному и тому же существенному признаку – основанию деления;

2) все подмножества не пересекаются;

3) Объединение всех подмножеств должно давать объем понятия;

4) для подмножеств (видов) множество должно быть ближайшим родовым понятием, а виды соподчиненными.

Отметим, что данное определение классификации относится к разновидности аксиоматических определений: четыре включенных в него требования выступают в роли аксиом – априорно присвоенных определяемому понятию свойств.

Наиболее простой классификацией является разбиение объема понятия на два класса – дихотомия, что в общем виде выглядит так. Пусть множество М состоит из элементов, каждый из которых обладает некоторым существенным свойством s (обозначение x(s)), или не обладает им (обозначение 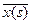). Разобьем множество М на два подмножества

, .

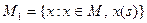Очевидно, что условия 1) – 4) выполняются.

Приведем примеры такой классификации.

1. Классификация понятия «треугольник» по соотношению между сторонами.

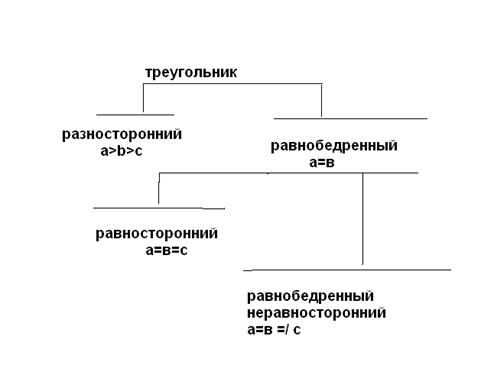
2. Классификация понятия «число».

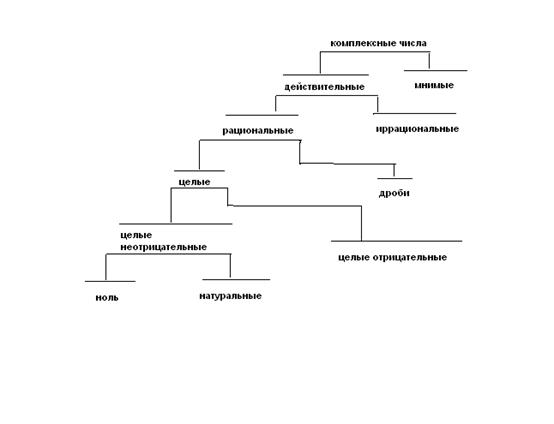
Упражнение. Привести классификацию понятия «отображение плоскости на себя».

Приведем пример классификации понятия «треугольник» по соотношению между углами, которая уже не будет дихотомией.

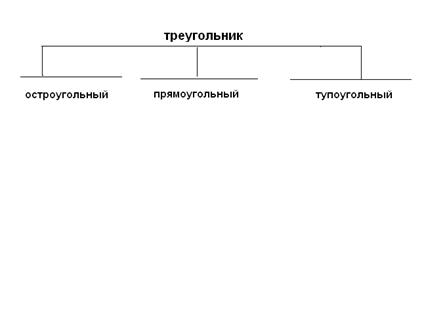
Классификация помогает правильно понять сущность понятий через выяснение их соотношений, разграничение объемов. Так первый пример классификации позволяет выявить часто встречающуюся у учащихся ошибку, когда они считают, что равносторонний треугольник не является равнобедренным.

Родословная понятия – это построение логического «дерева» возникновения понятия.

Например, родословная понятия «треугольник» отражает этапы формирования этого понятия, начиная от первичных понятий. Напомним определение. «Треугольником называется фигура, состоящая из трех точек, не лежащих на одной прямой, и трех отрезков, соединяющих эти точки.»

Чтобы построить родословную некоторого понятия, необходимо знать основные неопределяемые понятия, которые приведены в данном учебнике, а также основные отношения между ними и определения тех понятий, на которых базируется понятие, родословную которого мы строим.

Например, в учебнике В.В.Шлыкова «Геометрия 8» 2005 года издания основными неопределяемыми понятиями являются: точка, прямая, плоскость, множество. Затем вводятся понятия фигуры, отрезка, ломаной, простой ломаной, замкнутой ломаной.

Наконец дается следующее определение треугольника.

«Треугольником называется фигура, образованная трехзвенной замкнутой ломаной и ограниченной частью плоскости, для которой эта ломаная служит границей.»

Исходя из этого, мы можем построить следующую родословную понятия треугольник.

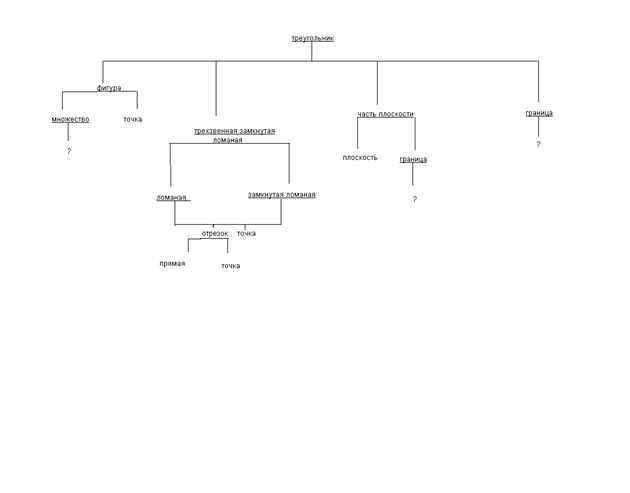
На этой диаграмме знаком вопрос отмечены те понятия, которые не сдержатся в учебнике.

Уже этот пример показывает, что умение составлять родословную понятия необходимый навык учителя. Он позволяет выделить неточные определения, а также помогает выделить те определения, которые необходимы для введения новых понятий.

Таблица 2.1

Характеристики наиболее распространённых CISC МП

Модель МП	Разрядность, бит	Тактовая частота, МГц	Адресное пространство, байт	Число команд	Число элемен- тов	Год выпус ка
данных	адреса
			4,77	64х103
			4,77; 8	106
	8; 16		4,77; 8	106
			8; 10	106
			10…33	4х106 виртуальное109
			25…50	16х106 виртуальное 4х106
			33…100	16х106 виртуальное 4х109		1,2х106
Pentium			50…150	4х109		3,1х106
Pentium Pro			66…200	4х109		5,5х106

Число элементов – это количество элементарных полупроводниковых элементов, размещённое в интегральной схеме МП.

Микропроцессор 80486 DX и все последующие модели могут работать с умножением внутренней частоты. Например, у МП DX2 внутренняя частота в 2 раза, а у МП DX4 – в 3 раза выше тактовой частоты. С увеличенной частотой работают только внутренние схемы МП, все внешние по отношению к МП схемы, в том числе расположенные на системной плате, работают с обычной частотой.

Отметим некоторые характеристики МП:

- начиная с МП 80386, используется конвейерное выполнение команд(одновременное выполнение разных тактов последовательных команд в разных частях МП при непосредственной передаче результатов из одной части МП в другую. Конвейерное выполнение команд увеличивает эффективное быстродействие ПК в 2-3 раза;

- начиная с МП80286, предусматривается возможность работы в вычислительной сети;

- начиная с МП80286, имеется возможность многозадачной работы (многопрограммность) и сопутствующая ей защита памяти;

- начиная с МП80386, обеспечивается поддержка режима системы виртуальных машин, т.е. такого режима многозадачной работы, при котором в одном МП моделируются как бы несколько компьютеров, работающих параллельно и имеющих разные операционные системы;

- начиная с МП 80286, микропроцессоры могут работать в двух режимах: реальном (Real mode) и в защищённом (Protected mode). В реальном режиме имитируется (эмулируется) работа МП 8086, естественно, однозадачная. В защищённом режиме возможна многозадачная работа (с непосредственным доступом к расширенной памяти и защитой памяти, отведённой задачам, от посторонних обращений.

Микропроцессоры 80586 (Р5) более известны по их товарной марке Pentium, которая запатентована фирмой Intel (МП 80586 других фирм имеют иные обозначения)

Эти микропроцессоры имеют пятиступенчатую конвейерную структуру, обеспечивающую многократное совмещение тактов выполнения последовательных команд, и КЭШ- буфер для команд условной передачи управления, позволяющий предсказывать направление ветвления программ; по эффективному быстродействию они приближаются к RISC МП, выполняющим каждую команду как бы за один такт. Pentium имеет 32- разрядную адресную шину и 64 - разрядную шину данных. Обмен данными с системой может выполняться со скоростью 1Гбайт/с.

У всех МП Pentium имеется встроенная КЭШ-память, отдельно для команд, отдельно для данных; имеются специализированные конвейерные аппаратные блоки сложения, умножения и деления, значительно ускоряющие выполнение операций с плавающей запятой.

Микропроцессоры Pentium Pro.

МП 80686 (Р6) благодаря новым схемотехническим решениям этот ПК имеет боле высокую производительность. Часть этих новшеств может быть объединена понятием динамическое исполнение (dynamic execution), что в первую очередь означает наличие 14- ступенчатой суперконвейерной структуры (superpipelining), предсказание и исполнение команд по предполагаемому пути ветвления (speculative execution).

В программах решения многих задач, особенно экономических, содержится большое число условных передач управления. Если процессор может заранее предсказать направление перехода (ветвления), то производительность его работы значительно повысится за счёт оптимизации загрузки вычислительных конвейеров. В процессоре Pentium Pro вероятность правильного предсказания 90% против 80% у МП Pentium.

КЭШ- память ёмкостью 256- 512 Кбайт – обязательный атрибут высокопроизводительных систем на процессорах Pentium. Однако у них встроенная КЭШ- память имеет небольшую ёмкость (16 Кбайт), а основная её часть находится вне процессора, на материнской плате. Поэтому обмен данными с ней происходит не на внутренней частоте МП, а на частоте тактового генератора, которая обычно в 2- 3 раза ниже, что снижает общее быстродействие компьютера. В МП Pentium Pro КЭШ- память ёмкостью 256- 512 Кбайт находится в самом микропроцессоре.