Применение симметрии относительно прямой при решении задач на построение

Определение. Пусть на плоскости задана прямая а и две точки А и В. Эти точки называются симметричными, если:

1) а ^ АВ;

2) прямая а делит отрезок пополам (рис. 9).

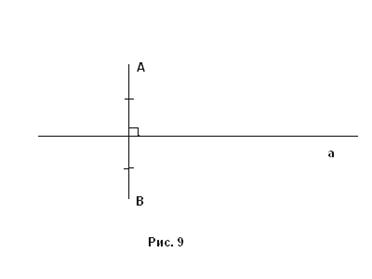
Прямая а при этом называется осью симметрии.

Определение. Отображение плоскости в себя называется симметрией относительно оси а или осевой симметрией, если каждой точке А плоскости ставится в соответствие симметричная ей точка А₁ относительно оси а.

Свойства осевой симметрии:

1). При осевой симметрии прямая переходит в прямую;

2). При осевой симметрии отрезок переходит в равный ему отрезок;

3). При осевой симметрии угол переходит в равный ему угол;

4). Осевая симметрия является движением.

Рассмотрим примеры применения симметрии.

ПРИМЕР 6. Дана прямая k и две точки А и В, не лежащие на этой прямой. На k найти такую точку Х, чтобы сумма АХ + ХВ была минимальной.

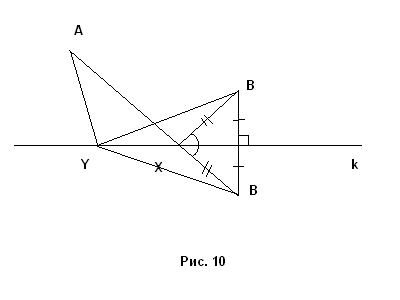
Анализ. Предположим, что задача решена. Если точки А и В расположены по разные стороны от К, то очевидно, что Х – это точка пересечения отрезка АВ и прямой k. Если же точки А и В по одну сторону от k, то отобразив В симметрично относительно k, получим точку В₁ такую, что ХВ = ХВ₁ и значит точка Х должна лежать на отрезке АВ₁ (рис. 10).

Построение. Если точки А и В по разные стороны от k, то проведем отрезок АВ и его пересечение с k есть искомая точка Х.

Если А и В по одну сторону от k, то отобразив В симметрично относительно k, получим точку В₁. Проведя отрезок АВ, получим искомую точку Х.

Доказательство. В первом случае доказательство очевидно. Во втором случае, когда А и В по одну сторону от k: пусть Y – любая другая точка прямой k, отличная от Х. Тогда из свойств симметрии получаем, что BY = B₁Y, а из неравенства треугольника имеем AY + YB = = АY + YB₁ > AB = AX + XB₁ (рис.10).

Исследование. Задача имеет решение всегда и причем одно.

ПРИМЕР 7. Построить четырехугольник АВСД, если заданы отрезки, являющиеся его сторонами АВ = a, ВС = b, СД = с, ДА = d и известно, что диагональ АС делит угол А пополам (рис. 11).

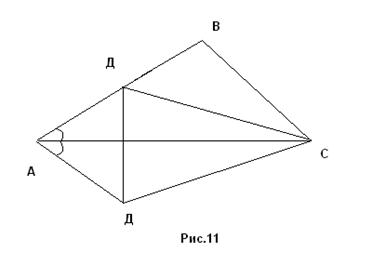
Анализ. Предположим задача решена и четырехугольник АВСД - искомый. Тогда из двух сторон АВ и АД одна больше. Пусть для определенности а > d. Отобразив симметрично точку Д относительно прямой АС получим на стороне АВ точку Д₁ . В треугольнике ВСД₁ известны все его стороны: ВС = b, СД = c, Д₁В = a – d. Значит треугольник Д₁ВС строится, а затем строится и весь четырехугольник.

Построение. Строим треугольник Д₁ВС по трем сторонам ВС = b, СД = с, Д₁В = а – d. Затем сторону ВД₁ продолжаем за точку Д₁ и от В откладываем отрезок АВ = а, получаем точку А. Построим точку Д, симметричную точке Д₁ относительно АС. Соединим точки А и Д, Д и С. Четырехугольник АВСД - искомый.

Доказательство. Очевидно из построения.

Анализ. Построение возможно, если возможно построить треугольник Д₁ВС, т.е. выполняются неравенства треугольника b < с + а + d, с < в + а – d, а – d < в + с. В этом случае задача имеет одно решение.