Признаки принадлежности хорошо известны из курса планиметрии. Наша задача рассмотреть их применительно к проекциям геометрических объектов.
Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости.
Принадлежность прямой плоскости определяется по одному из двух признаков:
а) прямая проходит через две точки, лежащие в этой плоскости;
б) прямая проходит через точку и параллельна прямой, лежащим в этой плоскости.
Используя эти свойства, решим в качестве примера задачу. Пусть плоскость задана треугольником АВС. Требуется построить недостающую проекцию D 1 точки D, принадлежащей этой плоскости. Последовательность построений следующая (рис. 2.5).
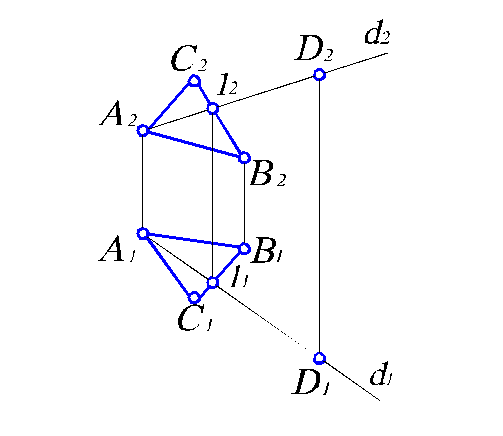

Через точку D 2 проводим проекцию прямой d, лежащей в плоскости DАВС, пересекающую одну из сторон треугольника и точку А 2. Тогда точка 12 принадлежит прямым А 2 D 2 и C 2 В 2. Следовательно, можно получить ее горизонтальную проекцию 11 на C 1 В 1 по линии связи. Соединив точки 11 и А 1, получаем горизонтальную проекцию d 1. Ясно, что точка D 1 принадлежит ей и лежит на линии проекционной связи с точкой D 2.
Достаточно просто решаются задачи на определение принадлежности точки или прямой плоскости. На рис. 2.6 показан ход решения таких задач. Для наглядности изложения задачи плоскость задаем треугольником.
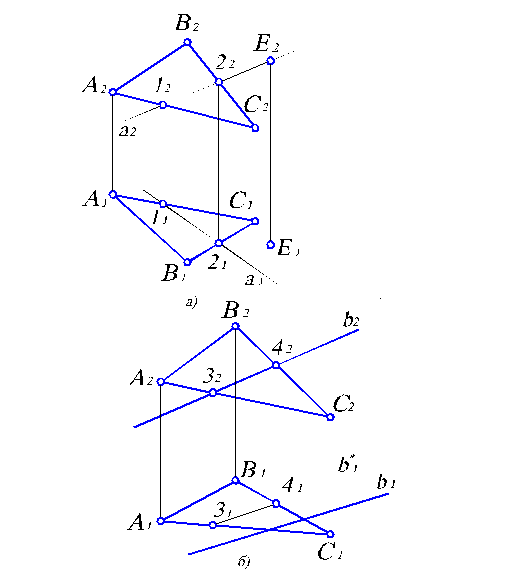
Рис. 2.6. Задачи на определение принадлежности точки и прямой плоскости.
Для того, чтобы определить принадлежит ли точка Е плоскости DАВС, проведем через ее фронтальную проекцию Е2 прямую а 2. Считая, что прямая а принадлежит плоскости DАВС, построим ее горизонтальную проекцию а 1 по точкам пересечения 1 и 2. Как видим (рис. 2.6, а), прямая а 1 не проходит через точку Е 1. Следовательно, точка Е ÏDАВС.
В задаче на принадлежность прямой в плоскости треугольника АВС (рис. 2.6, б), достаточно по одной из проекций прямой в 2 построить другую в 1* считая, что вÌDАВС. Как видим, в 1* и в 1 не совпадают. Следовательно, прямая в Ë DАВС.
 2014-02-09
2014-02-09 2262
2262
