Утверждение 3.
На интервале (xт-Δ,xт+Δ) существует только 1 корень уравнения (2).
Пусть существует 2 корня x1 и x2≠x1, тогда в силу (4) x1=φ(x1), x2=φ(x2). Из (6) следует | x2-x1|=|φ(x2)-φ(x1)|≤q|x2-x1|, т.е. |x2-x1|≤q|x2-x1|. Из этого следует, что q= 1, а это противоречит (7). Следовательно, корень только 1.
█
Следует так же отметить, что если φ(x) имеет на интервале (xт-Δ,xт+Δ) непрерывную производную, то (6) выполняется, когда
|φ′(x)|≤q => |φ′(x)|< 1для xÎ(xт-Δ,xт+Δ). (11)
Если |φ′(xт)|< 1, x0Î(xт-Δ,xт+Δ), то итерации сойдутся. Если |φ′(xт)|> 1, то в силу непрерывности производной |φ′(x)|> 1 и на некотором интервале (xт-Δ1,xт+Δ1), поэтому итерации не сойдутся к корню. Если же |φ′(xт)|< 1, но x0Ï(xт-Δ,xт+Δ), т.е. |φ′(x0)|> 1, то в данном случае о сходимости процесса можно судить только после дополнительного анализа функции φ(x).
Как и при поиске решения методом дихотомии будем считать задачу выполненной, если найденное некоторое значение xчÎ[xт-ε,xт+ε], где ε – заданная точность. Для определения того, когда можно прекратить итерации, т.е. когда достигнута заданная точность, подробнее рассмотрим неравенство (9). По сути, нам необходимо добиться выполнения следующего неравенства:
|
|
|
|xn+1-xт| ≤ ε, (12)
а в силу того, что из (9) можно получить неравенство |xn+1-xт| ≤ qn+1|x0-xт|, где q можно определить как 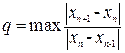 для любого целого n≥1, выведем условие достижения заданной точности (12). Введём обозначения δn+1=|xn+1-xт|. Из (9)
для любого целого n≥1, выведем условие достижения заданной точности (12). Введём обозначения δn+1=|xn+1-xт|. Из (9) 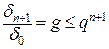 , а так же очевидно, что δ0-δn+1=|x0-xn+1|=ξ, тогда:
, а так же очевидно, что δ0-δn+1=|x0-xn+1|=ξ, тогда:
δ0=δn+1+ξ
δn+1=gδ=g(δn+1+ξ)
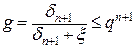
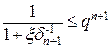
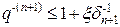
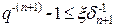
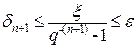
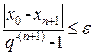 . (13)
. (13)
Неравенство (13) является условием остановки процесса итераций, т.е. условием достижения заданной точности. В завершение рассмотрения данного метода остаётся только построить блок-схему его алгоритма. Будем считать, что |φ′(xт)|<1, x0Î(xт-Δ,xт+Δ).

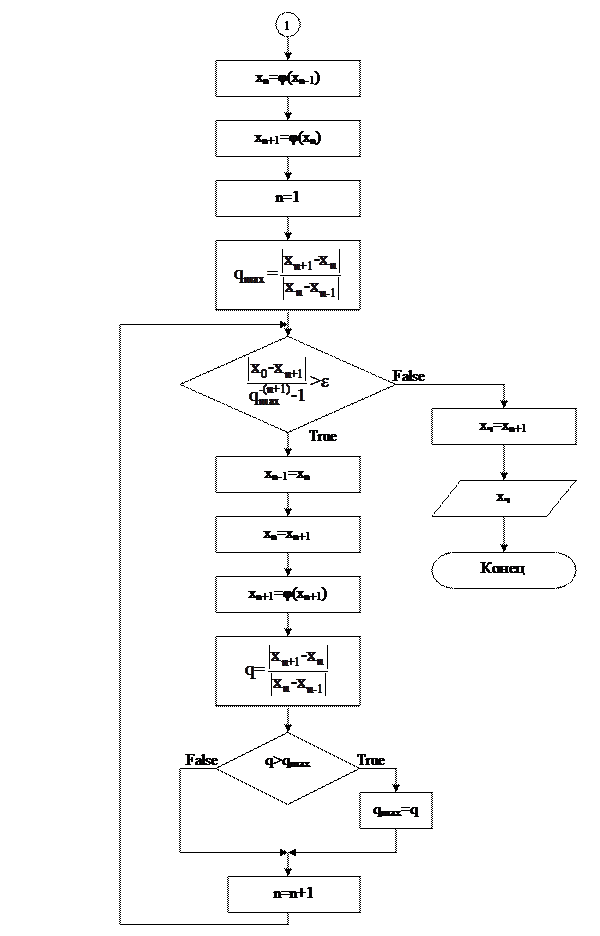
Метод касательных (Ньютона)
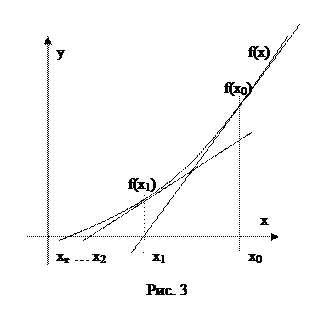
Метод Ньютона называют также методом касательных и методом линеаризации. Суть метода заключается в том, что в точке приближения к функции строится касательная (Рис. 3). Следующая точка приближения – это точка пересечения полученной прямой с осью Ox. Процесс продолжается вплоть до достижения заданной точности.
Из рисунка очень легко получить итерационную формулу метода, используя геометрический смысл производной. Если f(x) имеет непрерывную производную f’(x)≠0, тогда получим
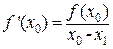
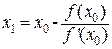
Аналогично получаем x2, x3, и т.д. Таким образом, можем записать общую формулу:
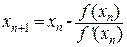
Метод Ньютона можно рассматривать, как частный случай метода простых итераций, если задать 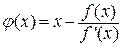 . В этом случае
. В этом случае 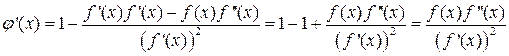 . Условие сходимости метода простых итераций можно переписать для метода Ньютона следующим образом:
. Условие сходимости метода простых итераций можно переписать для метода Ньютона следующим образом:
|
|
|
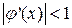
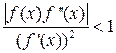
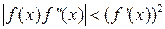 (14)
(14)
Рассуждения по поводу выбора начального приближения в методе Ньютона такие же, как и в методе простых итераций, только вместо (11) используется (14). Для данного метода также применимо (13). Напишем блок-схему алгоритма метода Ньютона.
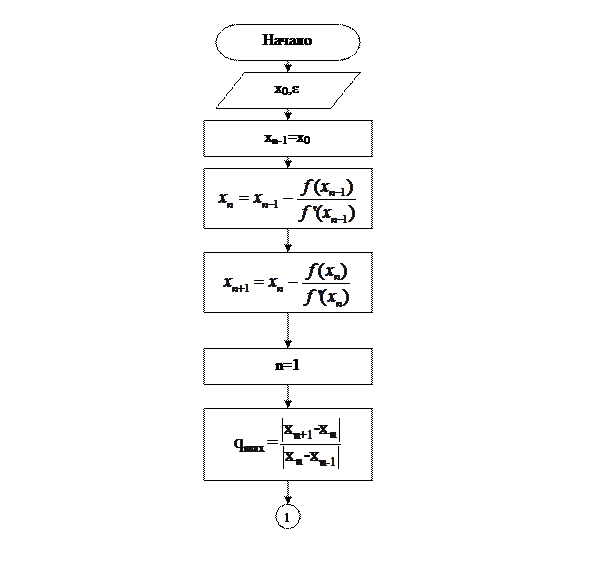

Метод секущих
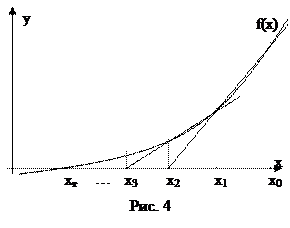
В данном методе, в отличие от метода Ньютона, проводятся не касательные, а секущие (Рис. 4). Из рисунка легко получить итерационную формулу:
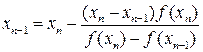 . (15)
. (15)
В качестве начального приближения необходимо задать не только x0, но и x1. Метод секущих имеет одно преимущество перед методом Ньютона – здесь не нужно вычислять производную. Но этот метод имеет также существенные недостатки. Сходимость итераций может быть немонотонной не только вдали от корня, но и в малой окрестности корня.
В знаменателе формулы (15) стоит разность значений функции. Вдали от корня это не существенно; но вблизи корня, особенно корня высокой кратности, значения функции малы и очень близки. Возникает потеря значащих цифр, приводящая к «разболтке» счёта. Это ограничивает точность, с которой можно найти корень; для простых корней это ограничение не велико, а для кратных может быть существенным.
От «разболтки» страхуются так называемым приёмом Гаврика. Выбирают не очень малое ε, ведут итерации до выполнения условия |xn+1-xn|<ε и затем продолжают расчёты до тех пор, пока |xn+1-xn| убывают. Первое же возрастание обычно означает начало «разболтки»; тогда расчёт прекращают и последнюю итерацию не используют.
Все ограничения по сходимости итераций для данного метода такие же, как и в методах простых итераций и Ньютона. А вот определение достижения заданной точности, как видно из описания метода, затруднительно, и, даже, возможна ситуация, когда из-за «разболтки» счёта заданная точность не будет достигнута никогда.
При использовании метода секущих в явном виде определить точность трудно, поэтому используют косвенный метод. Считают, что вблизи корня |xn+1-xn|~|x т -xn+1|. Конечно эта оценка весьма примерна, но при больших n (в идеале при n→∞) это так и есть. Построим блок-схему алгоритма данного метода с использованием приёма Гаврика.
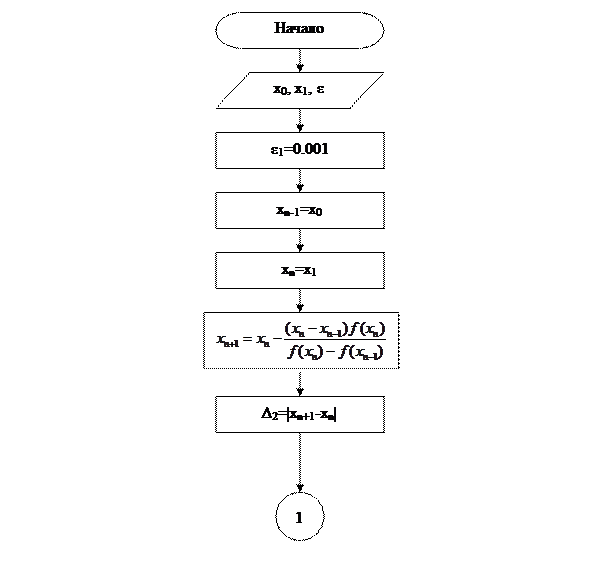
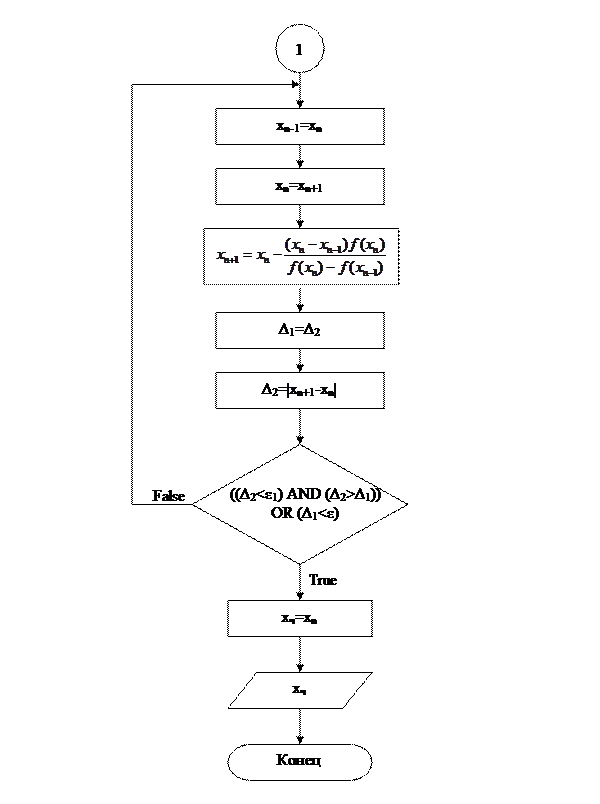
Численные методы вычисления определённых интегралов
Метод левых прямоугольников
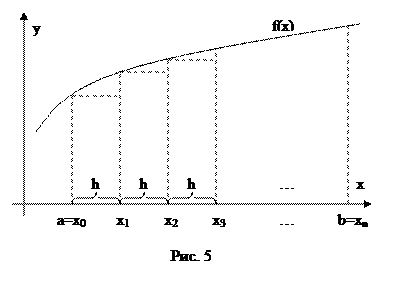 Эти методы численного интегрирования основываются на геометрическом смысле интеграла. Как известно интеграл
Эти методы численного интегрирования основываются на геометрическом смысле интеграла. Как известно интеграл 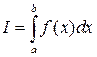 есть площадь криволинейной трапеции ограниченной подынтегральной функцией f(x) на отрезке [a,b]. Для вычисления интеграла I отрезок [a,b] разбивают на n отрезков длиной h. На каждом отрезке криволинейную трапецию приближают прямоугольником, так как его площадь можно легко вычислить. Затем суммируют все полученные площади, получая тем самым приближённое значение интеграла.
есть площадь криволинейной трапеции ограниченной подынтегральной функцией f(x) на отрезке [a,b]. Для вычисления интеграла I отрезок [a,b] разбивают на n отрезков длиной h. На каждом отрезке криволинейную трапецию приближают прямоугольником, так как его площадь можно легко вычислить. Затем суммируют все полученные площади, получая тем самым приближённое значение интеграла.
На рис. 5 проиллюстрирован, так называемый, метод левых прямоугольников. Его название объясняется тем, что высота прямоугольника f(x) вычисляется в левой границе отрезка h. Выведем формулу для приближённого вычисления интеграла I.
Как видно из рисунка площадь первого слева прямоугольника S0=f(x0)h. Площадь следующего S1=f(x1)h. Легко заметить, что площадь i -го прямоугольника Si=f(xi)h. Всего таких прямоугольников n, нумерация их ведётся от 0 до n -1. Таким образом, приближённое значение интеграла, полученное этим методом, вычисляется по формуле:
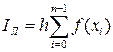 . (16)
. (16)
Оценим погрешность формулы (16) на отрезке [xi,xi+h]. Для этого разложим функцию f(x) по формуле Тейлора, выбирая xi за центр разложения и предполагая наличие у функции требуемых по ходу рассуждений непрерывных производных.
f(x)=f(xi)+(x-xi)f’(xi)+… (17)
В формуле (17) для определённости отбросим члены, содержащие производные высших порядков, т.е. 2-ю и выше. Тогда получим:
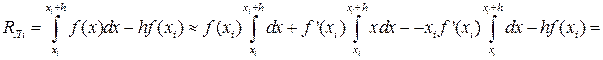
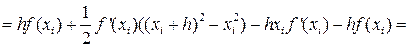
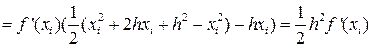 , т.е.
, т.е.
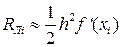 (18)
(18)
Чтобы получить общую погрешность метода на отрезке [a,b] просуммируем все RЛi:
|
|
|
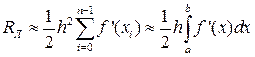 (19)
(19)
Поскольку в (17) были отброшены члены, содержащие более высокие степени длины интервала, то выражение остаточного члена (19) является асимптотическим, т.е. выполняющимся при h→0 с точностью до членов более высокого порядка малости. Но для справедливости этой оценки необходимо существование непрерывной f’(x); если f’(x) кусочно-непрерывна, то удаётся сделать лишь мажорантную оценку
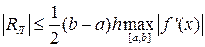 (20)
(20)
Эту формулу можно записать иначе
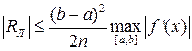 , (21)
, (21)
где n – количество отрезков, на которые разбит отрезок [a,b].
Перед началом вычислений по данному методу необходимо определиться с h или, что, по сути, то же самое, с n. Пусть известны границы отрезка [a,b], задана подынтегральная функция f(x) и точность ε, с которой должен быть вычислен интеграл. Чтобы определить h и n воспользуемся простым и очевидным неравенством:
|RЛ|≤ε,(22)
откуда получаем для непрерывной f’(x):
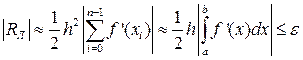
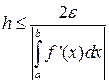 (23)
(23)
либо если учесть, что 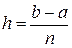 получим
получим
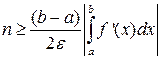 . (24)
. (24)
Для кусочно-непрерывной f’(x) с учётом (20) и (21) справедливо следующее
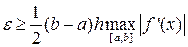
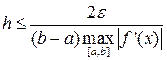 (25)
(25)
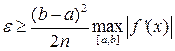
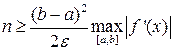 (26)
(26)
Метод правых прямоугольников
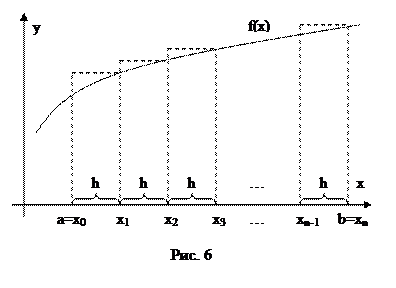 Этот метод похож на предыдущиу. Отличие в том, что высота прямоугольников вычисляется по правой границе (Рис. 6).
Этот метод похож на предыдущиу. Отличие в том, что высота прямоугольников вычисляется по правой границе (Рис. 6).
Выводы формул для данного метода аналогичны предыдущему. Основные отличия заключаются в нумерации. Формула метода правых прямоугольников выглядит следующим образом:
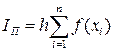 . (27)
. (27)
Рассуждения и конечные формулы, связанные с определением погрешности метода и выбором ширины основания прямоугольников аналогичны тому, что получено в предыдущем методе.
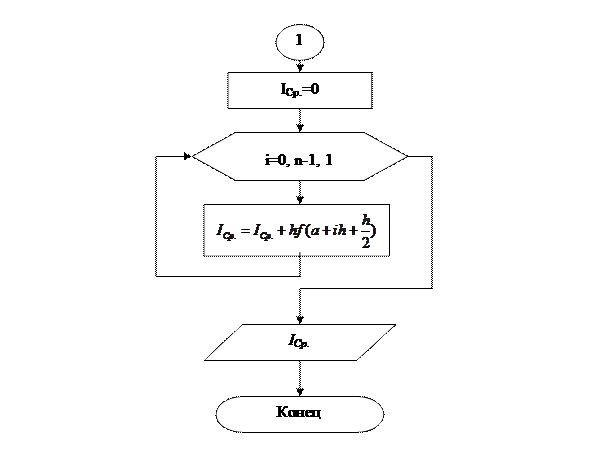
Метод средних прямоугольников
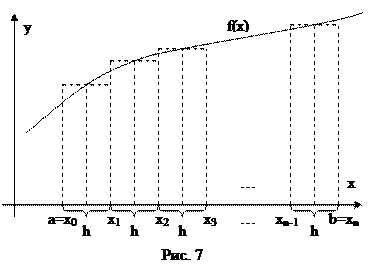 Чтобы уменьшить погрешность методов левых и правых прямоугольников был предложен метод средних, т.е. метод в котором высота прямоугольника вычисляется в середине отрезка h (Рис. 7). Обращаясь к рисунку легко увидеть, что площади прямоугольников вычисляются по следующим формулам:
Чтобы уменьшить погрешность методов левых и правых прямоугольников был предложен метод средних, т.е. метод в котором высота прямоугольника вычисляется в середине отрезка h (Рис. 7). Обращаясь к рисунку легко увидеть, что площади прямоугольников вычисляются по следующим формулам:
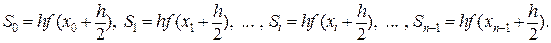
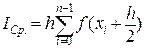 (28)
(28)
Оценим погрешность формулы (28) на отрезке [xi,xi+h]. Прежде всего, получим разложение по формуле Тейлора для данного метода. Центр разложения в данном случае будет точка 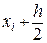 . Тогда получим:
. Тогда получим:
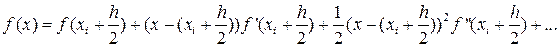 (29)
(29)
В формуле (29) отбросим члены, содержащие 3-ю и выше производные. Получаем:
|
|
|
Ii-IСр.i=RСр.i
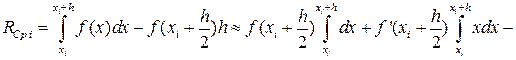
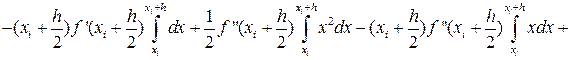
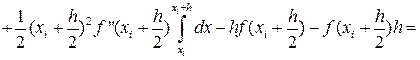
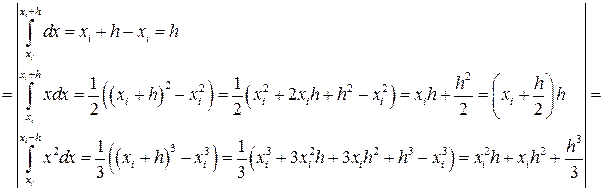
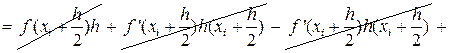
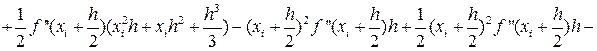
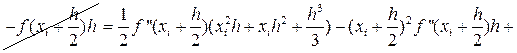
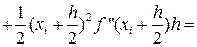
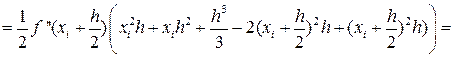
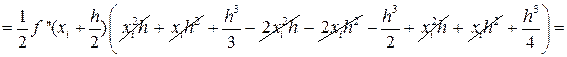
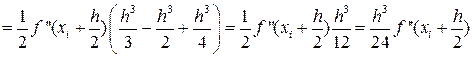 , т.е.
, т.е.
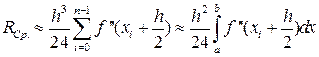 . (30)
. (30)
Аналогично тому, как были получены формулы (20), (21), (23), (24), (25) можно получить формулы, по которым оцениваются n и h, для данного метода. Запишем окончательные формулы для непрерывной f’’(x).
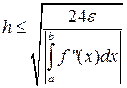 (31)
(31)
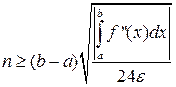 (32)
(32)
Для кусочно-непрерывной f’’(x) получаем мажорантные оценки:
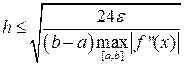 (33)
(33)
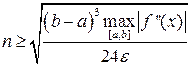 (34)
(34)
Сравнивая формулы (19) и (30) погрешностей методов приходим к выводу, что погрешность метода средних во много раз ниже погрешности метода левых или правых прямоугольников, т.е. метод средних во много раз точнее и для достижения заданной точности требует меньше машинного времени. Поэтому блок-схему построим именно для метода средних.
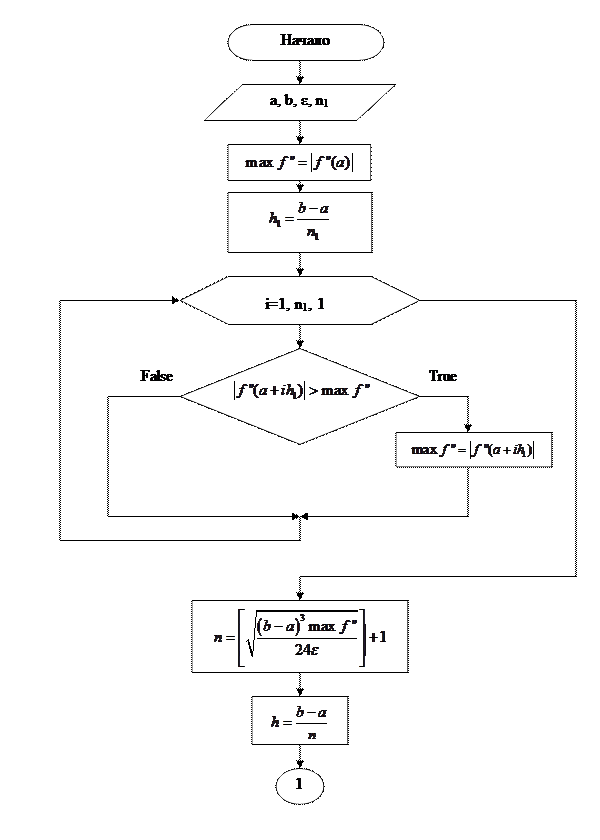
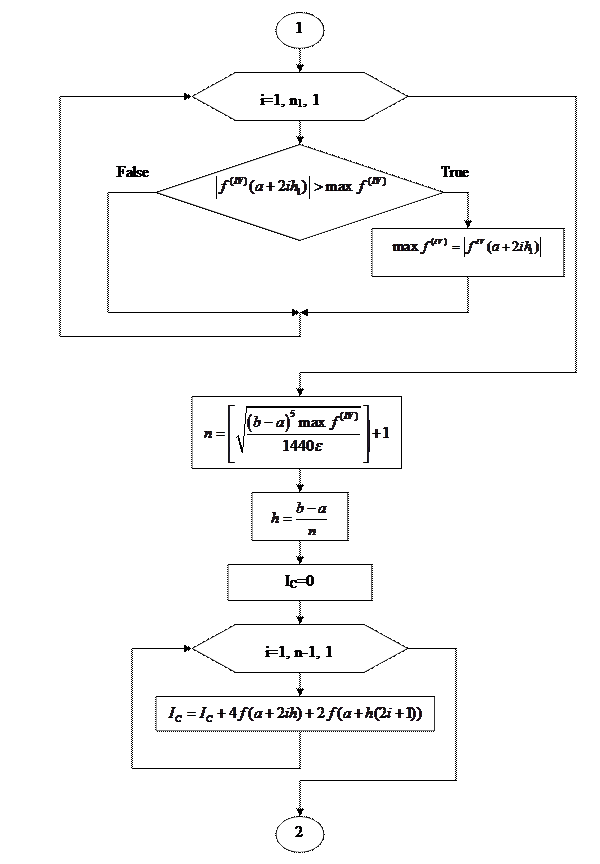
Введём обозначение. [n] – целая часть n, полученная путём отбрасывания дробно части. Для вычисления интеграла дано ε, [a,b], f(x), f’’(x). Прежде всего, через ε необходимо получить n. Пользоваться формулой (32) мы не будем, т.к. в ней необходимо вычислять интеграл. Воспользуемся мажорантной оценкой (34). Для этого перед вычислением интеграла необходимо найти 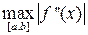 , но это легко осуществимо с помощью небольшого циклического процесса. Для него понадобиться знание количества разбиений
, но это легко осуществимо с помощью небольшого циклического процесса. Для него понадобиться знание количества разбиений 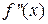 , на которых будем вычислять значения второй производной. Обозначим это количество n1.
, на которых будем вычислять значения второй производной. Обозначим это количество n1.
Метод трапеций
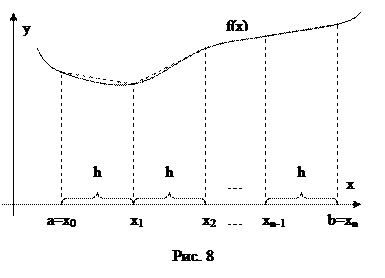 Метод трапеций основан на том, что криволинейная трапеция приближается прямолинейной (Рис. 8). Т.е. площади вычисляются по следующей формуле:
Метод трапеций основан на том, что криволинейная трапеция приближается прямолинейной (Рис. 8). Т.е. площади вычисляются по следующей формуле:
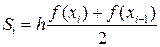
Таким образом, получаем общую формулу трапеций:
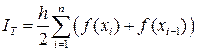 . (35)
. (35)
Теперь оценим погрешность метода. Вывод формулы погрешности аналогичен выводу (30), поэтому приведём сразу окончательную оценку погрешности для непрерывной f’’(x):
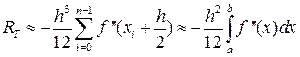 ; (36)
; (36)
для кусочно-непрерывной f’’(x):
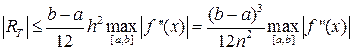 (37)
(37)
Оценивая n и h, получим:
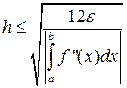 (38)
(38)
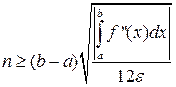 (39)
(39)
Для кусочно-непрерывной f’’(x):
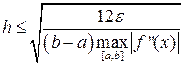 (40)
(40)
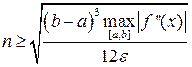 (41)
(41)
Как видно из полученных формул погрешность метода средних примерно вдвое меньше погрешности метода трапеций. Очевидно, что если функция определена на всём интервале, лучше пользоваться методом средних, метод трапеций используют обычно для функций определённых только в узлах сетки.
Знаки главного члена погрешности у формул трапеций и средних разные. Поэтому, если есть расчёты по обеим формулам, то точное значение интервала лежит, как правило, в вилке между ними. Деление этой вилки как 2:1 даёт уточнённый результат близкий к тому, который получается при использовании более точного метода Симпсона.
Метод Симпсона
Этот метод основан на том, что функция f(x) приближается на отрезке [xi-h, xi+h] параболой (причём xi отстоит от xi+1 на расстоянии 2h) (Рис.9). То есть через заданные точки проводится парабола. Но известно, что уравнение параболы имеет вид ρ(x)=ax2+bx+c, т.е. чтобы определить коэффициенты a, b, c необходимо решить систему из трёх уравнений, а для этого необходимо знать координаты как минимум трёх точек, через которые проходит парабола ρ(x). В связи с этим, в отличие от предыдущих методов, для вычисления площади отдельной криволинейной трапеции понадобиться не две, а три точки.
Для вывода формулы Симпсона рассмотрим подробнее i -ю криволинейную трапецию ограниченную сверху параболой ρi(x). Для упрощения расчётов сделаем следующие преобразования. Перенесём i -ю криволинейную трапецию в начало координат так, что xi= 0 (следовательно, xi-h=-h, xi+h=h). Очевидно, что её площадь не изменится. Найдём её площадь (Рис. 10). Для нахождения площади криволинейной трапеции необходимо знать форму кривой ограничивающей её. В нашем случае это парабола 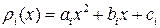 . Для нахождения коэффициентов ai, bi, ci составим систему из трёх уравнений. Для простоты обозначим ai≡a, bi≡b, ci≡c, f(xi-h)≡f0, f(xi)≡f1, f(xi+h)≡f1. Тогда
. Для нахождения коэффициентов ai, bi, ci составим систему из трёх уравнений. Для простоты обозначим ai≡a, bi≡b, ci≡c, f(xi-h)≡f0, f(xi)≡f1, f(xi+h)≡f1. Тогда
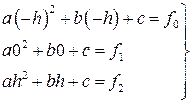
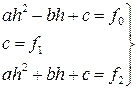
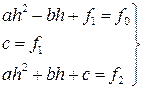
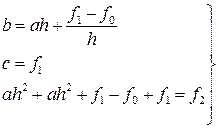
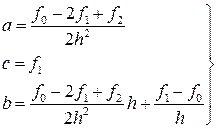
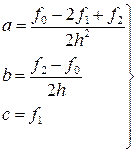
Таким образом, получаем
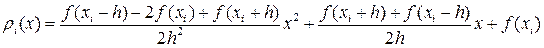 . (42)
. (42)
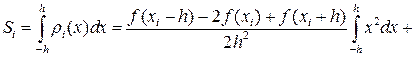
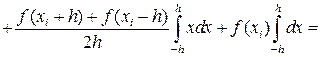
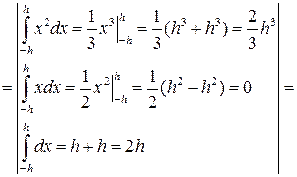
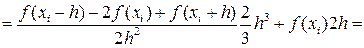
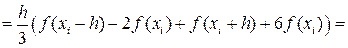
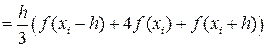 . (43)
. (43)
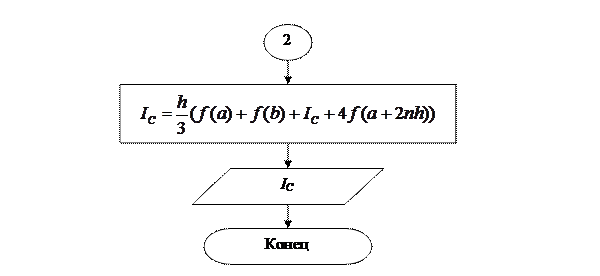
Таким образом, получаем общую формулу Симпсона:
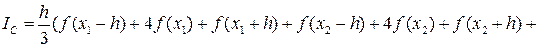
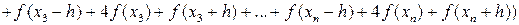
Для упрощения этой формулы учтём, что 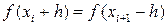 ,
, 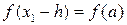 ,
, 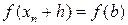 , где a и b – границы отрезка интегрирования [a, b]. С учётом этого получим:
, где a и b – границы отрезка интегрирования [a, b]. С учётом этого получим:
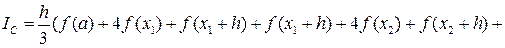
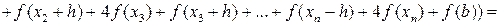
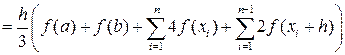 ,
,
где n – количество отрезков длиною 2h. То есть количество отрезков h, на которые разбит отрезок [a, b] должно быть обязательно чётным. Длина отрезка [a, b] равна 2nh.
Для оценки погрешности формулы Симпсона на отрезке [xi-h, xi+h] разложим функцию f(x) по формуле Тейлора до пятого члена с центром разложения в точке xi. То есть
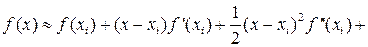
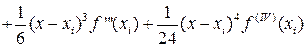 (44)
(44)
Тогда с учётом (43) и (44) получим:
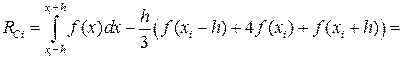
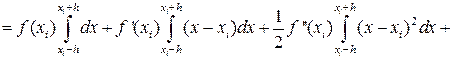
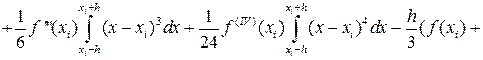
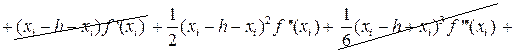
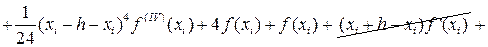
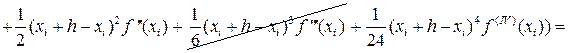
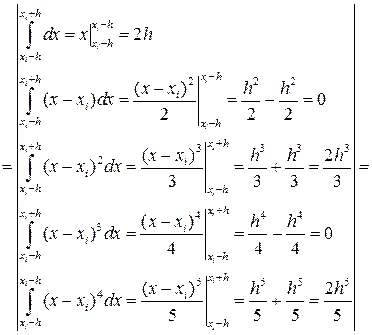
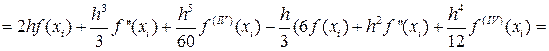
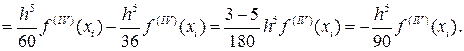
Т.е.
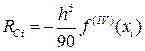
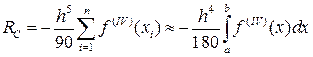 , (45)
, (45)
Сравнив формулы (45), (36), (30) и (19) увидим, что метод Симпсона является наиболее точным из всех описанных методов численного интегрирования.
Учитывая, что для метода Симпсона 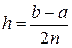 , запишем формулы оценки n и h для заданного ε. Для непрерывной
, запишем формулы оценки n и h для заданного ε. Для непрерывной 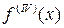 :
:
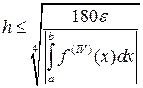 ,
,
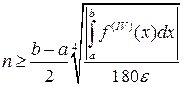 .
.
Мажорантные оценки для кусочно-непрерывной 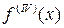 :
:
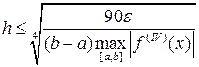 ,
,
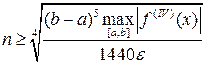 .
.
Построим блок-схему.

Приближение функций
Как известно, функцию можно задать многими способами. Самые распространённые из них – это аналитический, графический и табличный. В первых двух способах функция обычно определена на бесконечном числе точек, третий же способ задаёт лишь их конечное количество, например, экспериментальные данные или результаты сложных вычислений. В связи с этим встаёт вопрос получения промежуточных значений таблично заданной функции. Для их нахождения используют два способа: интерполяция (экстраполяция)* и аппроксимация.
При использовании интерполяции считают табличные значения точными и интерполяционный многочлен должен точно проходить через заданные точки (Рис. 11). Аппроксимирующая же функция лишь приближается как можно ближе к заданным точкам, но не обязательно через них проходит (Рис. 13). Это связано с тем, что табличные данные считаются приближенными, и точное прохождение функции через эти точки будет только увеличивать ошибку.
Интерполяция
Итак, как было сказано выше, задачей интерполяции является поиск такого многочлена, график которого проходит через заданные точки.
Пусть функция y=f(x) задана с помощью таблицы (табл. 1).
Таблица 1
| x | x0 | x1 | x2 | … | xn |
| y | y0 | y1 | y2 | … | yn |
 Необходимо получить многочлен Pn(x) такой, чтобы выполнялось условие:
Необходимо получить многочлен Pn(x) такой, чтобы выполнялось условие:
Pn(xi)=yi. (46)
Для этого зададимся конкретным видом многочлена. Пусть Pn(x) имеет следующий вид:
Pn(xi)=a0+a1x+a2x2+…+anxn. (47)
Для того, чтобы определить коэффициенты a0, a1,… необходимо решить систему из n уравнений с n неизвестными:
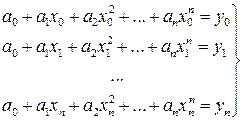 (48)
(48)
Полином с коэффициентами, полученными путём решения системы (48) называют интерполяционным полиномом Лагранжа и обозначают Ln(x). Решение системы (48) весьма трудоёмко, поэтому интерполяционный полином Лагранжа представляют в виде линейной комбинации многочленов степени n:

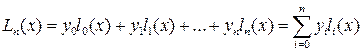 . (49)
. (49)
 Необходимо, чтобы каждый многочлен li(x) обращался в нуль во всех узлах интерполяции, за исключением i -го, в котором он равен 1 (Рис. 12). Если li(x) удовлетворяет таким условиям, то в i -ом узле интерполяции многочлен Ln(x) примет значение yi, что удовлетворяет условию поставленной задачи. Таким условиям удовлетворяет многочлен вида:
Необходимо, чтобы каждый многочлен li(x) обращался в нуль во всех узлах интерполяции, за исключением i -го, в котором он равен 1 (Рис. 12). Если li(x) удовлетворяет таким условиям, то в i -ом узле интерполяции многочлен Ln(x) примет значение yi, что удовлетворяет условию поставленной задачи. Таким условиям удовлетворяет многочлен вида:
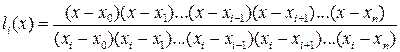 . (50)
. (50)
Таким образом, интерполяционный многочлен Лагранжа можно представить следующей общей формулой:
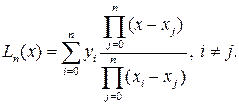 (51)
(51)
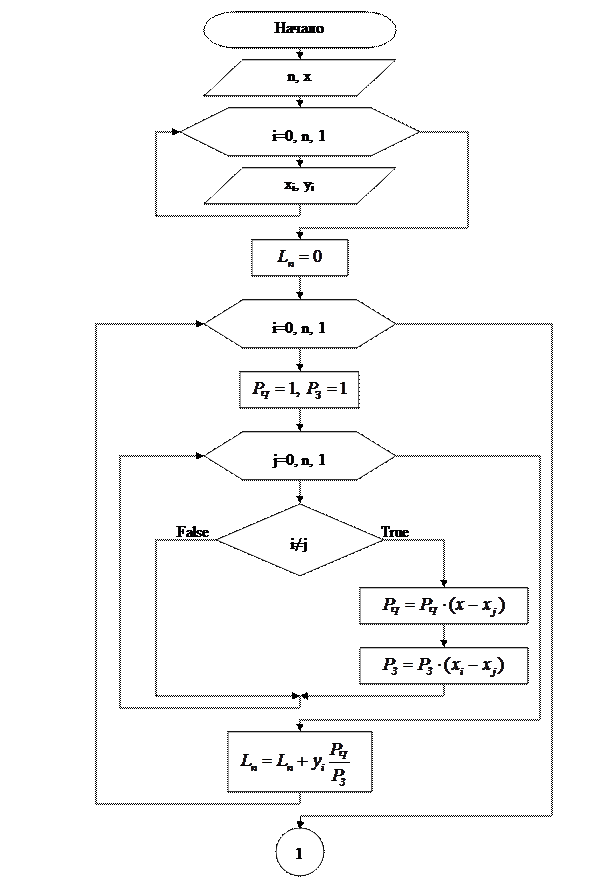
С использованием формулы (51) построим блок-схему алгоритма метода интерполяции функции полиномом Лагранжа.
Аппроксимация

В задачу аппроксимации входит нахождение такой функции y=f(x), что расстояния между заданными точками yi и значениями f(xi) были минимальными (Рис. 13). Обозначим отклонение:
εi=yi-f(xi)
В качестве оценки общего отклонения кривой f(x) от табличных данных (Табл. 1) можно было бы взять сумму отклонений εi, но отклонения могут быть разными по знаку и, не смотря на большие εi их сумма может быть близка к нулю. Очевидно, что необходимо брать сумму абсолютных значений отклонений, но на практике неудобно пользоваться этой функцией, поэтому в качестве критерия оценки отклонения кривой берут сумму квадратов отклонений:
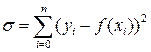 . (52)
. (52)
Для определения функции f(x) необходимо, во-первых, задать её общий вид, например, f(x)=ax+b, во-вторых, подставив f(x) в (52) и минимизировав σ, найти коэффициенты (a и b). Такой метод определения коэффициентов для функции f(x) называется методом наименьших квадратов. Наиболее часто встречающиеся виды функции f(x) для метода наименьших квадратов приведены в таблице 2. Формула y=f(x) называется эмпирической формулой или уравнением регрессии y на x.
Таблица 2
| Общий вид функции | Аналитическая формула | Вид регрессии |
| y=f(x,a,b) | y=ax+b | линейная |
| y=f(x,a,m) | y=axm | степенная |
| y=f(x,a,m) | y=aemx | показательная |
| y=f(x,a,b) | 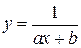
| дробно-линейная |
| y=f(x,a,b) | 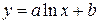
| логарифмическая |
| y=f(x,a,b) | 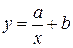
| гиперболическая |
| y=f(x,a,b) | 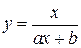
| дробно-рациональная |
Рассмотрим подробнее метод наименьших квадратов на примере линейной регрессии, т.е. общий вид функции такой: f(x)=ax+b. Требуется найти методом наименьших квадратов коэффициенты a и b. Для определения минимального σ необходимо приравнять нулю частные производные этой функции по параметрам a и b. Для случая линейной регрессии формула (52) приводится к следующему виду:
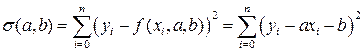 . (53)
. (53)
Условие экстремума запишется так:
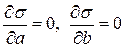 . (54)
. (54)
Отсюда получаем систему из двух уравнений с двумя неизвестными.
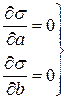 (55)
(55)
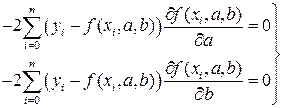 (56)
(56)
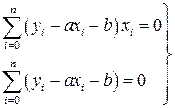
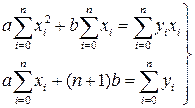
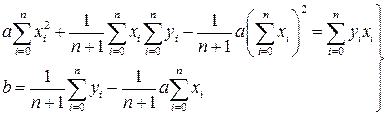
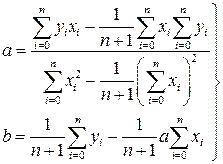
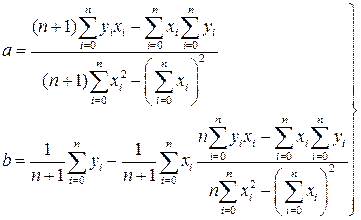
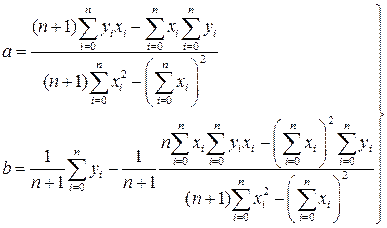
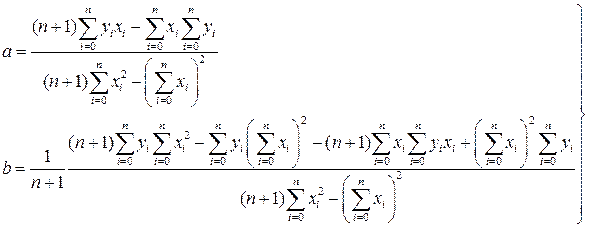
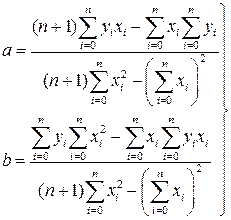 (57)
(57)
Итак, коэффициенты линейной регрессии вычисляются по формулам (57), но для определения параметров других видов регрессии выводить аналогичные формулы необязательно. Можно воспользоваться уже полученными. Для этого будем приводить все виды регрессии к линейному виду.
 2014-02-09
2014-02-09 2332
2332
