Метод половинного деления
Пусть дано уравнение
f(x)= 0, (8.1)
где функция f (х) непрерывна на [а, b] и f(а)f(b)<0.
Для нахождения корня уравнения (8.1), принадлежащего отрезку [а, b], делим этот отрезок пополам. Если 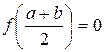 , то
, то 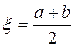 является корнем уравнения. Если
является корнем уравнения. Если 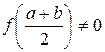 , то выбираем ту из половин
, то выбираем ту из половин 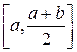 или
или  ,на концах которой функция f(х) имеет противоположные знаки. Новый суженный отрезок [a1 b1] снова делим пополам и проводим то же рассмотрение и т. д. В результате получаем на каком-то этапе или точный корень уравнения (8.1), или же бесконечную последовательность вложенных друг в друга отрезков [а1,b1], [а2, b2],…,[an, bп],... таких, что
,на концах которой функция f(х) имеет противоположные знаки. Новый суженный отрезок [a1 b1] снова делим пополам и проводим то же рассмотрение и т. д. В результате получаем на каком-то этапе или точный корень уравнения (8.1), или же бесконечную последовательность вложенных друг в друга отрезков [а1,b1], [а2, b2],…,[an, bп],... таких, что
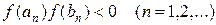 , (8.2)
, (8.2)
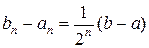 . (8.3)
. (8.3)
Так как левые концы а1, а2,... ап,... образуют монотонную неубывающую ограниченную последовательность, а правые концы b1, b2,…, bп —монотонную невозрастающую ограниченную последовательность, то в силу равенства (8.3) существует общий предел
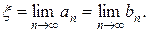
Переходя к пределу при n→∞ в неравенстве (8.2), в силу непрерывности функции f(х) получим [f(ξ)]2 ≤0. Отсюда f(ξ) = 0, т. е. ξ является корнем уравнения (8.1), причем, очевидно,
|
|
|
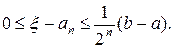 (8.4)
(8.4)
Если корни уравнения (8.1) не оделены на отрезке [а, b], то таким способом можно найти один из корней уравнения (8.1).
Метод половинного деления практически удобно применять для грубого нахождения корня данного уравнения, так как при увеличении точности значительно возрастает объем вычислительной работы.
Заметим, что метод половинного деления легко реализуется на ЭВМ. Программа вычисления составляется так, чтобы машина находила значение правой части уравнения (8.1) в середине каждого из отрезков [ an, bn ] (n=1, 2,...) и выбирала соответствующую половину его.
Пример 8.1. Методом половинного деления уточнить корень уравнения
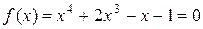 ,
,
лежащий на отрезке [0, 1].
Решение. Последовательно имеем:
f(0)=-1; f(1)=1;
f(0,5)=0,06+0,25-0,5-1=-1,19;
f(0,75)=0,32+0,84-0,75-1=-0,59;
f(0,875)=0,59+1,34-0,88-1=+0,05;
f(0,8125)=0,436+1,072-0,812-1=-0,304;
f(0,8438)=0,507+1,202-0,844-1=-0,135;
f(0,8594)=0,546+1,270-0,859-1=-0,043 и т.д.
Можно принять 
Метод Ньютона (метод касательных)
Пусть корень ξуравнения
f(х) = 0 (8.1)
отделен на отрезке [а, b], причем f ´(х) и f"(x) непрерывны и сохраняют определенные знаки при а≤ х≤b. Найдя какое-нибудь n -е приближенное значение корня xn ≈ξ (a ≤ хп ≤ b ), мы можем уточнить его по методу Ньютона следующим образом. Положим
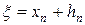 , (8.5)
, (8.5)
где hn считаем малой величиной. Отсюда, применяя формулу Тейлора, получим:
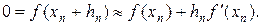
Следовательно, 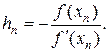
Внеся эту поправку в формулу (8.5), найдем следующее (по порядку) приближение корня
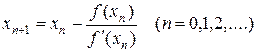 (8.6)
(8.6)
Геометрически метод Ньютона эквивалентен замене небольшой дуги кривой y = f(x) касательной, проведенной в некоторой точке кривой. В самом деле, положим для определенности, что f "(х)>0 при а≤х≤b и f(b)>0 (рис. 5).
|
|
|
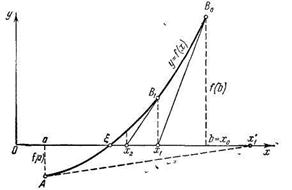 рис.5
рис.5
|
Выберем, например, хо = b, для которого f(х0) f " (х0) > 0. Проведем касательную к кривой у = f(x) в точке В0[х0, f(х0)].
В качестве пeрвого приближения x1 корня ξвозьмем абсциссу точки пересечения этой касательной с осью Ох. Через точку В1[х1, f(х1:)] снова проведем карательную, абсцисса точки пересечения которой даст нам второе приближение х2 корня ξ и т. д. (рис. 5). Очевидно, что уравнение касательной в точке Вп[хп, f(xn)] (n=0, 1, 2,...) есть
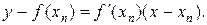
Полагая у = 0, х =хn+1, получим формулу (8.6)
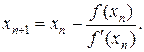
Заметим, что если в нашем случае положить х0 = а и, следовательно, f(х0)f"(х0)<0, то, проведя касательную к кривой y = f(x) в точке А[а, f (а)], мы получили бы точку х1 (рис. 5), лежащую вне отрезка [а, b], т. е. при этом выборе начального значения метод Ньютона оказывается непрактичным. Таким образом, в данном случае «хорошим» начальным приближением х0 является то, для которого выполнено неравенство
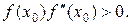
 2014-02-24
2014-02-24 2112
2112
