Графическое изображение электростатических полей

Для графического изображения электростатических полей используют линии вектора 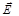- они проводятся так, чтобы в каждой точке вектор 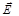был направлен по касательной к ним (рис. 6.2). Линии вектора 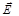нигде не пересекаются, они начинаются на положительных зарядах, заканчиваются на отрицательных или уходят в бесконечность. Примеры графического изображения полей точечных зарядов приведены на рис. 6.2б,в,г.

В случае однородного поля (рис. 6.2∂) в каждой точке которого вектор 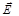одинаков и по модулю, и по направлению, линии 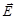представляют собой прямые, параллельные друг другу и отстоящие друг от друга на одинаковом расстоянии.

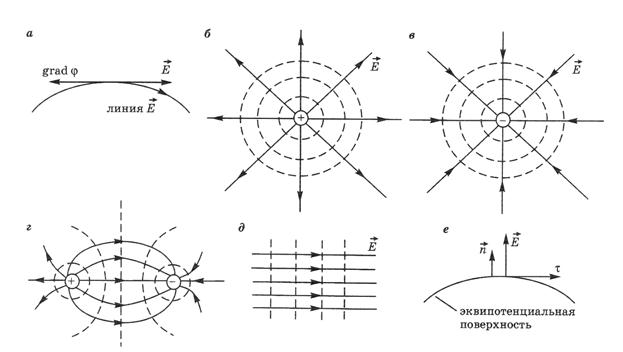
Рис. 6.2

Обычно линии 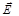проводят так, чтобы их густота в каждой точке поля определяла числовое значение вектора 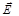. Под густотой линий 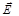понимают количество линий, пронизывающих перпендикулярную к ним плоскую поверхность фиксированной площади.

На рис. 6.2 пунктирными линиями изображены эквипотенциальные поверхности. Эквипотенциальная поверхность – это поверхность равного потенциала, в каждой точке поверхности потенциал φ будет одинаковым. Поэтому элементарная работа по перемещению заряда q по такой поверхности будет равна нулю: d A = – q d φ = 0. Соответственно вектор 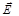в каждой точке поверхности будет перпендикулярен к ней, то есть будет направлен по вектору нормали 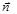(рис. 6.2е).

Условились проводить эквипотенциальные поверхности так, чтобы разность потенциалов между соседними поверхностями была одинаковой.

Лекция 7

7.1. Поток и циркуляция вектора 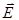электростатического поля.

Теорема Гаусса для вектора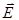

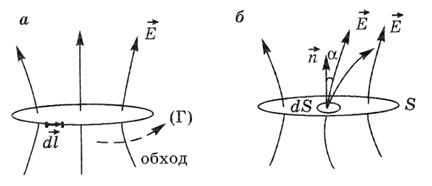
Возьмем произвольный контур Г и произвольную поверхность Sв неоднородном электростатическом поле (см. рис. 7.1а,б).

Рис. 7.1

Тогда циркуляцией вектора 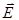по произвольному контуру Г называют интеграл вида

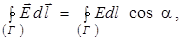(7.1)

а потоком Ф _Е вектора 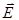через произвольную поверхность S следующее выражение:

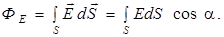(7.2)

Входящие в эти формулы векторы 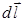и 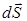определяются следующим образом. По модулю они равны элементарной длине dl контура Г и площади dS элементарной поверхности S. Направление вектора 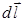совпадает с направлением обхода контура Г, а вектор 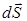направлен по вектору нормали 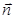к площадке dS (рис. 7.1).

В случае электростатического поля циркуляция вектора 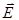по произвольному замкнутому контуру Г в соответствии с формулой (6.4) будет равна нулю:

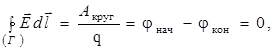(7.1а)

где А _круг – работа сил поля по перемещению точечного заряда qпо этому контуру.

Как отмечено в Прил., этот факт является признаком потенциальности электростатического поля. Следовательно, электрические заряды в электростатическом поле обладают потенциальной энергией.

Уравнение (7.1а) в дифференциальной форме, справедливой для малой окрестности какой-либо точки электростатического поля, можно записать следующим образом (см. Прил.):

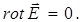(7.1б)

Теорема Гаусса в отсутствии диэлектрика (вакуум) формулируется следующим образом: поток вектора 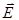через произвольную замкнутую поверхность равен алгебраической сумме свободных зарядов 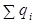, охватываемых этой поверхностью и деленной на ε₀:

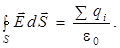(7.2)

Покажем справедливость теоремы для случая поля точечного заряда. Пусть замкнутая поверхность представляет собой сферу радиусом R, в центре которой находится точечный положительный заряд q (рис. 7.2а).

Рис. 7.2

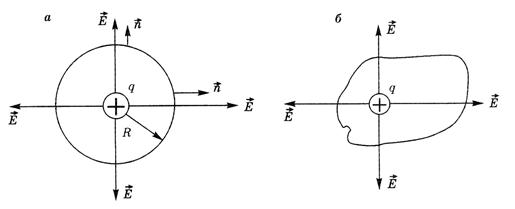
Тогда

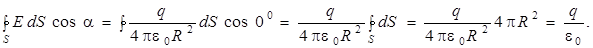(7.3)

Полученный результат не изменится, если вместо сферы выбрать произвольную замкнутую поверхность (рис. 7.2б), так как поток вектора 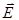численно равен количеству линий 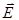, пронизывающих поверхность, а число линий 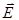в случаях (а)и (б) одинаково.

Подобные рассуждения с использованием принципа суперпозиции электростатических полей можно привести и в случае нескольких зарядов, попадающих внутрь замкнутой поверхности, что и подтверждает теорему Гаусса.

Запишем дифференциальную форму теоремы Гаусса, справедливую для любой малой окрестности какой-либо точки поля. С учетом формулы (П.10) Прил. получим

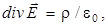(7.4)

где введена объемная плотность ρ свободных электрических зарядов

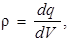
то есть это заряд, содержащийся в единице объема.

7.2. Применение теоремы Гаусса для расчета электростатических полей

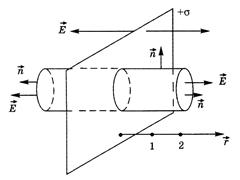
Пример 1. Электрическое поле равномерно заряженной по поверхности бесконечно протяженной плоскости.

Рис. 7.3

1-й этап. Введем поверхностную плотность заряда σ. Для этого на заряженной поверхности вблизи какой-либо ее точки выбирают элементарную площадку площадью dS, содержащую заряд dq, и рассчитывают по формуле

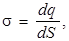
то есть σ представляет собой заряд, приходящийся на единицу поверхности. Если плоскость заряжена равномерно, то тогда во всех ее точках σ будет одинаковой (σ = const), и поэтому поле такой бесконечно протяженной плоскости является однородным – линии 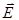представляют прямые, перпендикулярные к ней (рис. 7.3).

2-й этап. Выбираем замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к плоскости (рис. 7.3). Тогда поток Ф _Е через боковую поверхность будет равен нулю (α =90⁰, линии 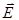не пересекают боковой поверхности), и поэтому остается поток только через основание площади S ₁ = S ₂ = S:

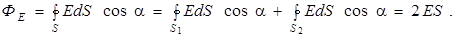
3-й этап. Рассчитаем заряд плоскости, попадающий внутрь цилиндра:

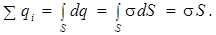
4-й этап. Применяем теорему Гаусса для расчета модуля вектора :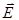

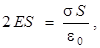
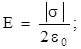(7.5)

здесь учтен случай отрицательно заряженной плоскости.

Формула (7.5) позволяет провести расчет поля плоского конденсатора как поля двух параллельных плоскостей с равными по модулю и противоположными по знаку поверхностными зарядами (рис. 7.4а).

Рис. 7.4

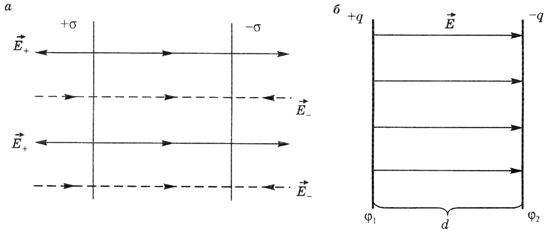
Используя принцип суперпозиции электростатических полей, можно сделать вывод о том, что поле конденсатора существует между его пластинами (рис. 7.4б), а модуль вектора этого поля

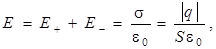(7.6)

где 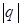- модуль заряда одной из пластин конденсатора площадью S. Между обкладками конденсатора вакуум или газ.

Оценим разность потенциалов φ ₁ – φ ₂ (или напряжение U) между обкладками конденсатора, находящимися на расстоянии d друг от друга. Для этого используем формулы (6.5) и (7.6):

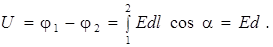(7.7)

Пример 2. Поле равномерно заряженной бесконечно длинной прямолинейной нити.

1-й этап. Введем линейную плотность заряда нити. Для этого на заряженной нити выбираем элемент длины dl, содержащий заряд dq, и рассчитаем τ по формуле

.

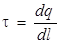Для равномерно заряженной нити во всех ее точках τ будет одинаковой (τ = const), поэтому поле такой нити обладает осевой симметрией: линии 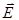представляют собой прямые, выходящие из нити и лежащие в плоскостях, перпендикулярных к ней (рис. 7.5а).

Рис. 7.5

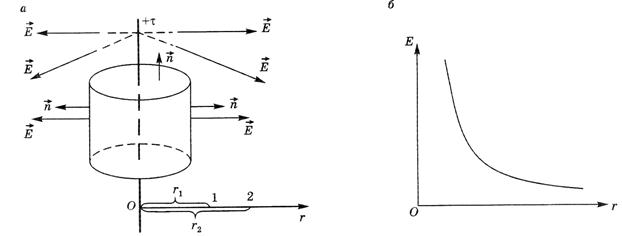
На одинаковых расстояниях от нити, то есть на цилиндрических поверхностях, модуль 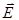будет одинаковым.

2-й этап. Выбираем замкнутую поверхность в виде цилиндра, имеющего высоту H и радиус r, ось цилиндра совпадает с нитью. Поток Ф _Е через основания цилиндра равен нулю (α=90⁰), поэтому остается поток только через боковую поверхность:

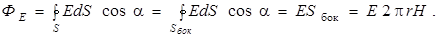
3-й этап. Рассчитаем заряд отрезка нити длины H, попадающий внутрь цилиндра:

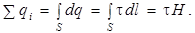
4-й этап. Применяем теорему Гаусса для расчета модуля вектора :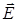

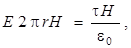
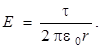(7.8)

Формула (7.8) позволяет оценить разность потенциалов между двумя точками, находящимися на расстояниях r ₁ и r ₂ от нити (рис. 7.5а):

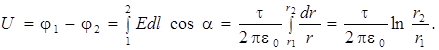(7.9)