Идентификация – единственность соответствия между приведенными и структурными формами модели.
Модели могут быть 3-х видов:
I. идентифицируемые,
II. неидентифицируемые,
III. сверхидентифицируемые,
Модель идентифицируема, если все ее структурные коэффициенты определяются однозначно, единственным образом по коэффициентам приведенной формы модели, т.е. число параметров структурной модели равно числу параметров приведенной формы.
Модель неидентифицируема, если число приведенных коэффициентов меньше числа структурных коэффициентов.
Модель сверхидентифицируема, если число приведенных коэффициентов больше числа структурных коэффициентов. В этом случае на основе коэффициентов приведенной формы можно получить 2 или более значений 1 структурного коэффициента.
Структурная модель всегда представляет собой систему совместных уравнений, каждое из которых требуется проверить на идентифицируемость.
Модель считается идентифицтруемой, если каждое уравнение системы идентифицируемо. Если хотя бы одно уравнение неидентифицируемо, то и вся система считается неидентифицируемой. Если модель содержит хотя бы одно сверхидентифицируемое уравнение, при условии, что все остальные точно идентифицируемы, то вся модель считается сверхидентифицируемой.
Cчетное правило (т.е. необходимое условие идентификации).
H - число эндогенных переменных в уравнении,
D - число предопределенных уравнением переменных, отсутствующих в данном уравнении, но присутствующих в системе
Если D+1=H - система идентифицируема,
Если D+1<H - система неидентифицируема,
Если D+1>H - система сверхидентифицируема.
Пример. Имеется система уравнений:
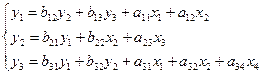
Проверяем необходимое условие идентификации
| уравнение | H | D | неравенство | характеристика уравнения |
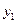 , , , ,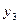
| 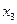 , ,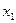
| 2+1=3 | идентифицируема | |
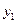 , ,
| 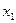 , ,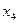
| 2+1>2 | сверхидентифицируема | |
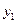 , , , ,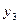
| 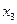
| 1+1<3 | неидентифицируема |
Система неидентифицируема, т.к. уравнение 3 идентифицируемо, и не имеет статистическое решение.
Достаточное условие идентификации
По этому условию более точно определяется идентификация модели.
Определитель матрицы, составленный из коэффициентов при переменных, отсутствующих в уравнении, но присутствующих в системе
(всех переменных: экзогенных и эндогенных), не равен 0 и ранг этой матрицы не менее числа эндогенных переменных системы без 1.
Пример:
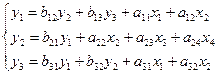
1)Проверим необходимое условие идентификации (его соблюдение)
1 уравнение: H = 3; D = 2, 2+1=3 идентифицируемо
2 уравнение: H = 2; D = 1, 1+1=2 идентифицируемо
3 уравнение: H = 3; D = 1, 2+1=3 идентифицируемо
В соответствии с необходимым условием, модель считается идентифицируемой.
| уравнение | переменные | |
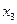
| 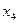
| |
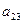
| 
| |
2)Проверим на достаточное условие идентификации 1 уравнение:
 , следовательно, уравнение 1 неидентифицируемо.
, следовательно, уравнение 1 неидентифицируемо.
| уравнение | переменные | |
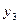
| 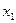
| |
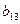
| 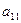
| |
| -1 | 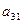
|

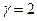 , что соответствует обоим критериям достаточного условия, следовательно уравнение идентифицируемо.
, что соответствует обоим критериям достаточного условия, следовательно уравнение идентифицируемо.
| уравнение | переменные | |
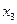
| 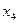
| |
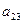
| 
|
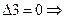 уравнение неидентифицируемо.
уравнение неидентифицируемо.
Структурная модель, идентифицируемая по счетному правилу (по необходимому условию), оказалась неидентифицируема по достаточному условию
Система неидентифицируема.
4. Способ решения точно идентифицированной системы (косвенный МНК)
Коэффициенты структурной формы модели могут быть оценены разным способами в зависимости от вида системы одновременных уравнений. В случае точной идентифицированной структурной модели применяется косвенный МНК, который состоит из следующих этапов:
1) структурная модель преобразуется в приведённую форму.
2) для каждого уравнения приведённой формы обычным МНК оценивается приведённые коэффициенты 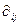 .
.
3) коэффициенты приведённой формы модели трансформируются в параметры структурной модели.
Пример: структурная форма модели.
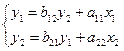
Имеется информация по данным переменным по 5 регионам.
| регион | 
| 
| 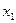
| 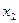
|
| среднее | 6,2 | 2,4 | 3,4 |
1) Приведенная форма модели
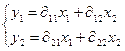
Для каждого уравнения приведённой формы модели используем традиционный МНК и определяем 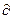 коэффициенты.
коэффициенты.
Для упрощения расчётов будем работать с отклонениями от средних уравнений.
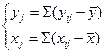
Для I уравнения ПФМ система нормальных уравнений (МНК) составит
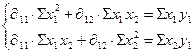
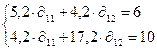
Решив данную систему уравнений, получим

Следовательно:
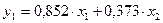
Аналогично, применяя МНК ко II уравнению получаем систему нормальных уравнений (МНК)
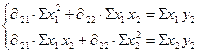 ;
;
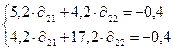
Решая данную систему получаем:
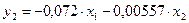
ПФМ имеет вид
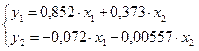
2)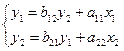 - СФМ.
- СФМ.
Работаем с первым уравнением СФМ, Должны выразить коэффициенты 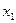 и
и 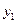 через коэффициенты
через коэффициенты 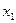 и
и 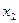 ПФМ.
ПФМ.
В первом уравнении ПФМ нет  , т.е. необходимо исключить
, т.е. необходимо исключить 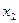 из приведенной формы модели и выразить его через
из приведенной формы модели и выразить его через  .
.
Выразим 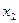 из второго уравнения приведенной формы.
из второго уравнения приведенной формы.
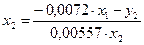
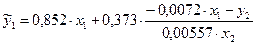
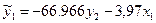
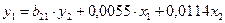
 2014-02-09
2014-02-09 3418
3418