Постановка задачи. Открытая и закрытая модель

Транспортная задача является задачей наиболее рациональ­ного прикрепления пунктов назначения к пунктам отправления, чтобы транспортные издержки были минимальными.

Пример транспортной задачи рассматривался во введении. В общей постановке она выглядит следующим образом.

Имеется m пунктов отправления с запасами a_i единиц груза в каждом. Имеется n пунктов назначения с потребностями в грузах b_j. Стоимость перевозки одной единицы груза по соответствующему маршруту равна c_ij.

Матрица (c_ij)_mxn называется матрицей тарифов (транспортных расходов).

Планом транспортной задачи называется матрица X = (x _ij)_mxn, где каждое число x_ij обозначает количество единиц груза, кото­рое надо доставить из i -го пункта отправления в j -й пункт на­значения. Матрица X называется еще матрицей перевозок. Чаще всего матрицы тарифов и перевозок совмещают в одну двойную матрицу (табл. 2).

Таблица 2.

Матрица стоимости и перевозок общий вид

Пункты назначения Пункты отправления	B1	B2	…	Bj	…	Bn	Запасы груза
A1	с11 х11	с12 х12	…	с1j х1j	…	с1n х1n	a1
А2	с21 х21	с22 х22	…	с2j х2j	…	с2n х2n	a2
…	…	…	…	…	…	…	…
Аi	сi1 хi1	сi2 хi2	…	сij хij	…	сin хin	ai
…	…	…	…	…	…	…	…
Аm	сm1 хm1	сm2 хm2	…	сmj хmj	…	сmn хmn	am
Потребности в грузе	b1	b2	…	bj	…	bn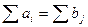

Стоимость перевозок z можно записать в виде двойной суммы

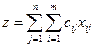. (1)

Это и будет функционалом задачи, для которого надо отыскать минимум.

На искомые перевозки x_ij по смыслу задачи необходимо наложить следующие условия:

1) условия вывоза всех грузов из пунктов отправления (m уравнений):

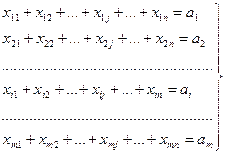(2)

2) условия доставки потребителям необходимого количества грузов (n уравнений):

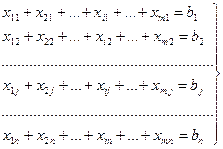(3)

3) условия неотрицательности переменных, исключающие обратные перевозки:

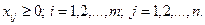(4)

Эти условия образуют систему ограничений. Любой план, ком­поненты которого удовлетворяют этой системе, будет допусти­мым.

Равенство запасов потребностям есть необходимое и доста­точное условие совместности и, следовательно, разрешимости транспортной задачи.

Транспортная задача, в которой выполнено указанное усло­вие, называется сбалансированной (закрытой).

Однако может случиться, что в рассматриваемых пунктах запасы не равны потребностям: или 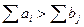, т. е. запасы пре­восходят потребности, или же 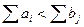— запасы не обеспечи­вают потребностей.

Такая модель задачи называется несбалансированной (открытой). Для нее тоже можно отыскать план с минимумом транспортных расходов, но не будут удовлетворены потребности или не будет вывезен весь груз, так как нельзя подобрать такую систему чисел, которая при суммировании по строкам давала бы один результат, а при суммировании по столбцам — другой.

Для решения задачи поступаем следующим образом.

Первый случай. 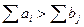. В математическую модель транспортной задачи введем фиктивный (n + 1)-й пункт назна­чения. Для этого в матрице задачи предусмотрим один столбец (табл. 3), для которого потребность будет равна излишку груза:

.

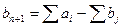Таблица 3

Добавление фиктивного пункта назначения

Пункты назначения Пункты отправления	B1	B2	…	Bn	Bn+1	Запасы груза
A1	с11 х11	с12 х12	…	с1n х1n	0 х1,n+1	a1
А2	с21 х21	с22 х22	…	с2n х2n	0 х2,n+1	a2
…	…	…	…	…	…	…
Аm	сm1 хm1	сm2 хm2	…	сmn хmn	0 хm,n+1	am
Потребности в грузе	b1	b2	…	bn	bn+1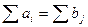

Все тарифы на доставку груза в этот пункт будем считать равными нулю. Получим новую задачу, причем для старой и новой задачи функционал будет один и тот же, так как цены на дополнительные перевозки равны нулю:

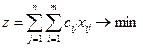
Фиктивный потребитель обеспечивает совместность системы ограничений, не внося искажений в решение.

Второй случай. Если запасов не хватает для удовлетво­рения потребностей, т. е. 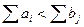, то вводим фиктивный (m + 1)-й пункт отправления, которому приписываем запас груза, равный

,

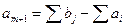тарифы на доставку грузов из этого фиктивного склада опять, полагаем нулевыми. В матрице добавится одна строка (табл. 4)

Таблица 4.

Добавление фиктивного склада

Пункты назначения Пункты отправления	B1	B2	…	Bn	Запасы груза
A1	с11 х11	с12 х12	…	с1n х1n	a1
А2	с21 х21	с22 х22	…	с2n х2n	a2
…	…	…	…	…	…
Аm	сm1 хm1	сm2 хm2	…	сmn хmn	am
Аm+1	0 хm+1,1	0 хm+1,2	…	0 хm+1,n	am+1
Потребности в грузе	b1	b2	…	bn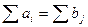

на функционале это не отразится, а система ограничений задачи станет совместной, т. е. станет возможным отыскание оптималь­ного плана на минимум стоимости перевозок.

Транспортная задача имеет такую специфику.

1. Ограничения заданы уравнениями (всего m+n уравнений).

2. Каждое неизвестное плана входит только в два уравне­ния. Неизвестное x_ij входит в уравнение с правой частью a_i и в уравнение с правой частью b_j.

3. Коэффициентами в уравнениях являются единицы.