2014-02-12
3072
Пусть имеем дифференциальное уравнение первого порядка: y′ = f (x, y). Для такого уравнения Теорема о существовании и единственности решения принимает вид:
| Теорема: (1.1) | Если функция и ее частная производная  непрерывны в некоторой области D плоскости OXY, содержащей точку (x 0, y 0), то существует единственное решение этого уравнения y = φ (x), удовлетворяющее условию: φ (x 0)= y 0.
|
Замечание: доказательство Теоремы представлено в Пособии, ее понимание и толкование на экзамене предполагается!
Заметим, что получение решения ДУ в виде явной функции y = φ (x) следует рассматривать как самый простой случай, который не часто наблюдается. Учитывая возможности вычисления неопределенных интегралов, следует учесть также, что «берущихся интегралов» совсем немного. Это значит, что получить аналитическое выражение решения чаще не удается. Мы будем считать, что ДУ решено даже в случае, когда удалось просто расставить символы интегрирования! Все эти случаи объединим одним общим «выражением»:
Ф(x,y,С)=0 – общий интеграл (С – произвольная постоянная).
Имея определение «общего решения», определим понятие «частного» решения ДУ.
| Определение: (1.4) | Частным решением дифференциального уравнения n-го порядка называется: 1). Функция y = y (x,С 1 ,С 2,…, С n) решения ДУ при любых частных значениях постоянных С 1 ,С 2,…, С n; 2). Любая функция, которая обращает ДУ в тождество. |
Выражение Ф(x,y,С)=0 общего интеграла ДУ при С = С 0 называют частным интегралом. Так как на плоскости OXY решение y = y (x,С) при любом значении С изображается кривой, то каждую их них называют интегральной кривой. То же говорят и в случае использования выражения Ф(x,y,С)=0.
Восприятию Теоремы 1.1 способствует использование понятий «поле направлений» и «изоклины». Воспользуемся дифференциальным уравнением в виде: y′ = f (x, y).
Поле направлений: если выделена некоторая точка плоскости (x 0, y 0), то это определяет число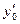 
= k 0= f (x 0, y 0). Учитывая, что геометрический смысл производной – угловой коэффициент касательной к кривой в выделенной точке, можем сказать, что уравнение y′ = f (x, y) определяет «поле направлений» на плоскости OXY. Это поле можно сделать видимым в выделяемых точках, если в каждой точке построить коротенькую черточку.
Изоклины: линия, определяемая уравнением k 0= f (x,y), называется изоклиной, так как в каждой ее точке направление поля, определяемого уравнением y′ = f (x, y), имеет постоянную величину k 0. Использование изоклины для построения поля направлений бывает удобно, так как все «черточки» касательных на ней параллельны!
