Пример 9 классической линейной моделью множественной регрессии

РАЗДЕЛ V. МНОЖЕСТВЕННАЯ ЛИНЕЙНАЯ РЕГРЕССИЯ

Построение функциональной связи между результирующим показателем и двумя и более факторами носит название множественной (многофакторной, многомерной) регрессии. Зависимую переменную обычно называют результативным признаком, а независимые переменные ¾ факторами.

В случае множественной регрессии выбор формы связи оказывается значительно более сложным по сравнению с парной регрессией.

Практика построения многофакторных моделей показывает, что реально существующие в экономике зависимости можно описать, используя следующие типы моделей:

1) линейную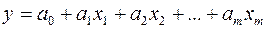

2) степенную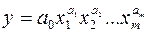

3) экспоненциальную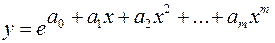

4) параболическую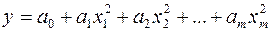

5) гиперболическую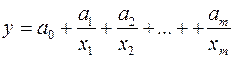

Основное значение имеют линейные модели (относительно параметров регрессии) в силу своей простоты. Нелинейные формы зависимости часто преобразуются к линейным путем линеаризации.

Для модели множественной линейной регрессии должны выполнять следующие предпосылки:

1) математическое ожидание случайного отклонения 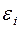(остаток в i -м наблюдении) равно нулю для всех наблюдений;

2) дисперсии отклонений постоянны и равны для всех наблюдений;

3) случайные отклонения независимы друг от друга;

4) случайное отклонение независимо от объясняющих переменных;

5) модель линейна относительно параметров;

6) между факторами отсутствует строгая линейная связь;

7) случайные отклонения 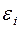распределены нормально с параметрами 0 и .

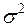Первые четыре условия носят название условия Гаусса-Маркова.

Если для модели выполнены все условия, то она называется классической нормальной моделью множественной регрессии.

Если для модели выполнены все условия, кроме последнего, то она называется классической линейной моделью множественной регрессии.

Следует заметить, что если при построении регрессионной модели добавляются новые значения, то величины 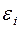могут изменяться, так как при этом будут изменяться коэффициенты регрессии. Поэтому регрессионный анализ включает в себя не только построение самой модели, но и исследование остатков. При этом сами остатки 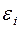рассматриваются как случайные величины.

Пакет MS Excel позволяет при построении уравнения линейной регрессии большую часть работы сделать очень быстро. Важно понять, как интерпретировать полученные результаты.

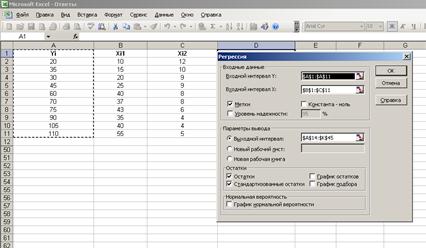
Для построения модели регрессии необходимо выбрать пункт Сервис\Анализ данных\Регрессия. (В Excel 2007 этот режим находится в блоке Данные/Анализ данных/ Регрессия). Появится диалоговое окно, которое нужно заполнить:

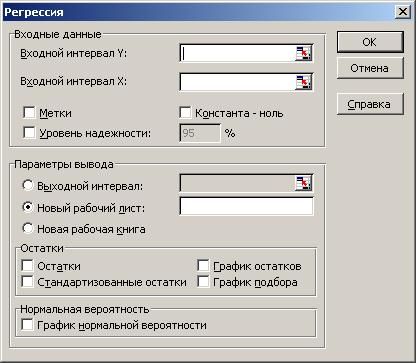
1) Входной интервал Y ¾ содержит ссылку на ячейки, которые содержат значения результативного признака y. Значения должны быть расположены в столбце;

2) Входной интервал X ¾ содержит ссылку на ячейки, которые содержат значения факторов 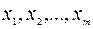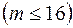. Значения должны быть расположены в столбцах;

3) Признак Метки ставится, если первые ячейки содержат пояснительный текст (подписи данных);

4) Уровень надежности ¾ это доверительная вероятность, которая по умолчанию считается равной 95%. Если это значение не устраивает, то нужно включить этот признак и ввести требуемое значение;

5) Признак Константа-ноль включается, если необходимо построить уравнение, в котором свободная переменная ;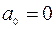

6) Параметры вывода определяют, куда должны быть помещены результаты. По умолчанию строит режим Новый рабочий лист;

7) Блок Остатки позволяет включать вывод остатков и построение их графиков.

В результате выводится информация, содержащая все необходимые сведения и сгруппированная в три блока: Регрессионная статистика, Дисперсионный анализ, Вывод остатка. Рассмотрим их подробнее.

1. Регрессионная статистика:

множественный R определяется формулой 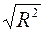(коэффициент корреляции Пирсона);

R -квадрат вычисляется по формуле 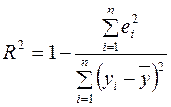(коэффициент детерминации);

Нормированный R -квадрат вычисляется по формуле 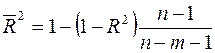(используется для множественной регрессии);

Стандартная ошибка S вычисляется по формуле ;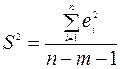

Наблюдения ¾ это количество данных n.

2. Дисперсионный анализ, строка Регрессия:

Параметр df равен m (количество наборов факторов x);

Параметр SS определяется формулой ;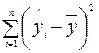

Параметр MS определяется формулой ;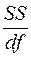

Статистика F определяется формулой ;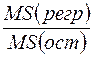

Значимость F. Если полученное число превышает 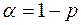, то принимается гипотеза 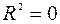(нет линейной взаимосвязи), иначе принимается гипотеза 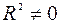(есть линейная взаимосвязь).

3. Дисперсионный анализ, строка Остаток:

Параметр df равен ;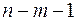

Параметр SS определяется формулой ;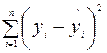

Параметр MS определяется формулой .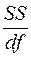

4. Дисперсионный анализ, строка Итого содержит сумму первых двух столбцов.

5. Дисперсионный анализ, строка Y-пересечение содержит значение коэффициента 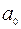, стандартной ошибки 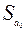и t -статистики .

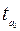P -значение ¾ это значение уровней значимости, соответствующее вычисленным t -статистикам. Определяется функцией СТЬЮДРАСП(t -статистика; 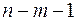). Если P -значение превышает 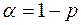, то соответствующая переменная статистически незначима и ее можно исключить из модели.

Нижние 95% и Верхние 95% ¾ это нижние и верхние границы 95-процентных доверительных интервалов для коэффициентов теоретического уравнения линейной регрессии. Если в блоке ввода данных значение доверительной вероятности было оставлено по умолчанию, то последние два столбца будут дублировать предыдущие. Если пользователь ввел свое значение доверительной вероятности, то последние два столбца содержат значения нижней и верхней границы для указанной доверительной вероятности.

6. Дисперсионный анализ, строки 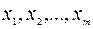содержат значения коэффициентов, стандартных ошибок, t -статистик, P -значений и доверительных интервалов для соответствующих .

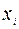7. Блок Вывод остатка содержит значения предсказанного y (в наших обозначениях это 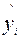) и остатки .

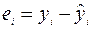Предполагается, что объем предложения товара y линейно зависит от цены товара 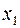и зарплаты сотрудников 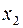. Статистические данные приведены в таблице:

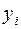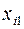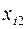а) построить методом МНК уравнение регрессии;

б) найти стандартную ошибку регрессии и стандартные ошибки коэффициентов;

в) найти доверительные интервалы коэффициентов теоретического уравнения линейной регрессии, доверительная вероятность 95%;

г) определить статистическую значимость коэффициентов теоретического уравнения линейной регрессии, доверительная вероятность 95%;

д) проверить общее качество уравнения линейной регрессии, доверительная вероятность 95%.

Решение.

Вводим заданные значения 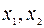и y, затем выбираем пункт меню Сервис\Анализ данных/Регрессия. Далее указываем интервалы значений x и y, включаем режим Метки, оставляем уровень надежность по умолчанию, указываем выходной интервал и включаем вывод остатков:

Получаем результат:

д)

б)

д)

г)

в)

б)

а)

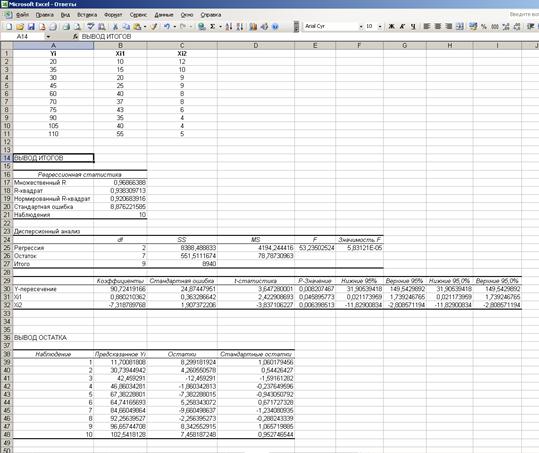
а) Коэффициенты уравнения 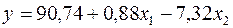, соответствуют данным столбца Коэффициенты.

б) Стандартная ошибка регрессии, равная 8,88, соответствует значению Стандартная ошибка блока Регрессионная статистика.

Стандартные ошибки коэффициентов 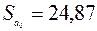, , 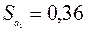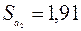соответствуют значениям столбца Стандартная ошибка блока Дисперсионный анализ.

в) Доверительные интервалы соответствуют интервалам

; ; .

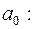
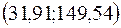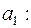
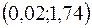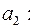
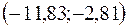г) Статистическая значимость коэффициентов уравнения определяется с помощью P-значений из соответствующего столбца. Они все меньше значения a = 0,05, следовательно, все коэффициенты статистически значимы.

д) Коэффициент детерминации равен 0,94 (в блоке Регрессионная статистика он называется R-квадрат). Это означает, что наша модель объясняет 94% общего разброса значений результативного признака. Скорректированный (нормированный) коэффициент детерминации равен 0,92. Это означает, что наша модель объясняет 92% общего разброса значений результативного признака с учетом поправки на число степеней свободы.

Проверяем статистическую значимость коэффициента детерминации с помощью значения Значимость F, которое меньше значения a = 0,05. Следовательно, коэффициент детерминации статистически значим.

Итог: полученное уравнение объясняет 92% общего разброса значений результативного признака, что с вероятностью 95% является качественным результатом. Данную модель можно использовать для прогнозирования.