2015-01-30
8227
Пример 8.1 В семи случаях из десяти фирма-конкурент компании "А" действовала на рынке так, как будто ей заранее были известны решения, принимаемые фирмой "А". На уровне значимости 0,05 определите, случайно ли это, или в фирме "А" работает осведомитель фирмы-конкурента?
Решение. Для того чтобы ответить на вопрос данной задачи, необходимо проверить статистическую гипотезу о том, совпадает ли данное эмпирическое распределение числа действий фирмы-конкурента с равномерным теоретическим распределением?
Если ходы, предпринимаемые конкурентом, выбираются случайно, т.е. в фирме "А" - нет осведомителя (инсайдера), то число "правильных" и "неправильных" ее действий должно распределиться поровну, т.е. по 5 (10/2). А это и есть отличительная особенность равномерного распределения.
Этот вид статистических гипотез относится к гипотезам о виде закона распределения генеральной совокупности. 
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
|
|
|
Н0: Х~R(a; b) - случайная величина Х подчиняется равномерному распределению с параметрами (a; b) (в контексте задачи - "в фирме "А" - нет осведомителя (инсайдера)"; "распределение числа удачных ходов фирмы-конкурента - случайно").
Н1: Случайная величина Х не подчиняется равномерному распределению (в контексте задачи - "в фирме "А" - есть осведомитель (инсайдер)"; "распределение числа удачных ходов фирмы-конкурента - не случайно").
В качестве критерия для проверки статистических гипотез о неизвестном законе распределения генеральной совокупности используется случайная величина c2. Этот критерий называют критерием Пирсона.
Его наблюдаемое значение (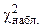
) рассчитывается по формуле:
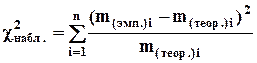, (8.1)
где m(эмп.)i - эмпирическая частота i-той группы выборки;
m(теор.)i - теоретическая частота i-той группы выборки.
Составим таблицу распределения эмпирических и теоретических частот:
| m(эмп.)i | ||
| m(теор.)i |
Найдем наблюдаемое значение :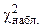
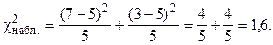
Критическое значение (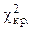
) следует определять по таблице распределения c2 (см. приложение 4) по уровню значимости a и числу степеней свободы k.
По условию a = 0,05, а число степеней свободы рассчитывается по формуле:
k = n - l - 1,
где k - число степеней свободы;
n - число групп выборки;
l - число неизвестных параметров предполагаемой модели, оцениваемых по данным выборки (если все параметры предполагаемого закона известны точно, то l = 0).
По условию задачи число групп выборки (n) равно 2, т.к. могут быть только два варианта действий фирмы-конкурента: "удачные" и "неудачные", а число неизвестных параметров равномерного распределения (l) равно 0.
|
|
|
Отсюда, k = 2 - 0 - 1 = 1.
Найдем 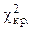по уровню значимости a = 0,05 и числу степеней свободы k=1.
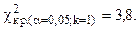
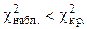, следовательно, на данном уровне значимости нулевую гипотезу нельзя отклонить, расхождения эмпирических и теоретических частот - незначимые. Данные наблюдений согласуются с гипотезой о равномерном распределении генеральной совокупности.
Это означает, что для утверждения о том, что действия фирмы-конкурента на рынке неслучайны; на уровне значимости a = 0,05 можно утверждать, что в фирме "А" нет платного осведомителя фирмы-конкурента.
Ответ. на уровне значимости a = 0,05 можно утверждать, что в фирме "А" нет платного осведомителя фирмы-конкурента.
Пример 8.2 На уровне значимости a = 0,025 проверить гипотезу о нормальном распределении генеральной совокупности, если известны эмпирические и теоретические частоты:
| m(эмп.)i | ||||||
| m(теор.)i |
Решение. Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: Х~N(a; s2) - случайная величина Х подчиняется нормальному закону распределения с параметрами а и s2.
Н1: Случайная величина Х не подчиняется нормальному закону распределения с параметрами а и s2.
В качестве критерия для проверки нулевой гипотезы используем критерий Пирсона c2.
Найдем наблюдаемое значение ():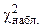
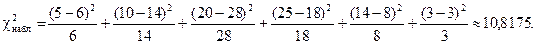
Найдем критическое значение критерия (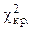) по таблице распределения c2 (приложение 4) по уровню значимости a и числу степеней свободы k.
По условию a = 0,025; число степеней свободы найдем по формуле:
k = n - l - 1,
где k - число степеней свободы;
n - число групп выборки;
l - число неизвестных параметров предполагаемой модели, оцениваемых по данным выборки.
По условию задачи число групп выборки (n) равно 6, а число неизвестных параметров нормального распределения (l) равно 2.
Отсюда, k = 6 - 2 - 1 = 3.
Найдем 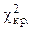по уровню значимости a = 0,025 и числу степеней свободы k=3.
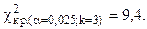
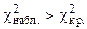, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей, расхождения эмпирических и теоретических частот - значимые. Данные наблюдений не согласуются с гипотезой о нормальном распределении генеральной совокупности.
Ответ. На уровне значимости a = 0,025 данные наблюдений не согласуются с гипотезой о нормальном распределении генеральной совокупности.
Пример 8.3 Техническая норма предусматривает в среднем 40 сек. на выполнение определенной технологической операции на конвейере по производству часов. От работниц, работающих на этой операции, поступили жалобы, что они в действительности затрачивают на эту операцию больше времени. Для проверки данной жалобы произведены хронометрические измерения времени выполнения этой технологической операции у 16 работниц, занятых на этой операции, и получено среднее время выполнения операции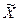 
= 42 сек. Можно ли по имеющимся хронометрическим данным на уровне значимости a = 0,01 отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, если:
а) исправленное выборочное среднее квадратическое отклонение s составило 3,5 сек.;
б) выборочное среднее квадратическое отклонение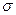 
составило 3,5 сек.?
Решение. а) Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна определенному числу, когда дисперсия генеральной совокупности неизвестна ( выборка мала, т.к. n = 16, меньше 30).
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: a = а0 = 40 - неизвестное математическое ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) равно гипотетическому предполагаемому числовому значению а0 (применительно к условию данной задачи - время выполнения технологической операции соответствует норме).
|
|
|
Н1: a > 40 - неизвестное математическое ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) больше числовому значению а0 (применительно к условию данной задачи - время выполнения технологической операции больше установленной нормы).
Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.
В качестве критерия для сравнения неизвестного математического ожидание а (нормально распределенной генеральной совокупности с неизвестной дисперсией) с гипотетическим числовым значением а0, используется случайная величина t - критерий Стьюдента:
Его наблюдаемое значение (tнабл.) рассчитывается по формуле:
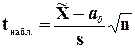. (8.2)
где 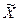- выборочная средняя;
а0 - числовое значение генеральной средней;
s - исправленное среднее квадратическое отклонение;
n - объем выборки.
Найдем наблюдаемое значение tнабл.:
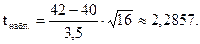
Критическое значение (tкр.) следует находить по таблице распределения Стьюдента (приложение 5) по уровню значимости a и числу степеней свободы k.
По условию a = 0,01; число степеней свободы найдем по формуле:
k = n - 1,
где k - число степеней свободы;
n - объем выборки.
k = 16 - 1 = 15.
Найдем tкр. по уровню значимости a = 0,01 (для односторонней критической области) и числу степеней свободы k = 15:
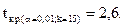
Заметим, что при левосторонней конкурирующей гипотезе Н1: a < 40 tкр. следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для односторонней критической области) и числу степеней свободы k = n - 1 и присваивать ему "минус";
При двусторонней конкурирующей гипотезе Н1: a ¹ 40 tкр. следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для двусторонней критической области) и числу степеней свободы k = n - 1).
tнабл. < tкр, следовательно, на данном уровне значимости нет оснований отклонить нулевую гипотезу.
Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 нельзя отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме. Следовательно, жалобы работниц - необоснованны.
|
|
|
 |
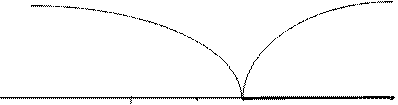Область допустимых Критическая
значений область
t
0 tнабл.= 2,29 tкр.= 2,6
Рис 8.4.
Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нет оснований отклонить нулевую гипотезу.
б) Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна определенному числу, когда дисперсия генеральной совокупности неизвестна.
Алгоритм решения задачи будет тот же, что и в первом случае. Однако наблюдаемое значение tнабл. будет рассчитывается по формуле:
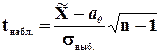. (8.3)
где 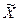- выборочная средняя;
а0 - числовое значение генеральной средней;
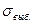- выборочное среднее квадратическое отклонение;
n - объем выборки.
Найдем наблюдаемое значение (tнабл.):
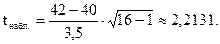
Критическое значение (tкр.) следует находить по таблице распределения Стьюдента (приложение 5) по уровню значимости a и числу степеней свободы k.
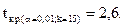
tнабл. < tкр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу, жалобы работниц - необоснованны.
Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 нельзя отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, жалобы работниц - необоснованны.
Пример 8.4 Изменим условие предидущей задачи. Техническая норма предусматривает в среднем 40 сек. на выполнение определенной технологической операции на конвейере по производству часов. От работниц, работающих на этой операции, поступили жалобы, что они в действительности затрачивают на эту операцию больше времени. Для проверки данной жалобы произведены хронометрические измерения времени выполнения этой технологической операции у 36 работниц, занятых на этой операции, и получено среднее время выполнения операции 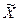= 42 сек. Можно ли (предполагая время выполнения технологической операции случайной величиной, подчиняющейся нормальному закону) по имеющимся хронометрическим данным на уровне значимости a = 0,01 отклонить гипотезу о том, что среднее время выполнения этой операции соответствует норме, если известно, что среднее квадратическое отклонение генеральной совокупности s составляет 3,5 сек.?
Решение. Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная средняя нормальной совокупности точно равна числовому значению, когда дисперсия генеральной совокупности известна (большая выборка, т.к. n = 36, больше 30).
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: a = а0 = 40 - неизвестная генеральная средняя нормально распределенной совокупности с известной дисперсией равна числовому значению (применительно к условию данной задачи - время выполнения технологической операции соответствует норме).
Н1: a > 40 - неизвестная генеральная средняя нормально распределенной совокупности с известной дисперсией больше числового значения (применительно к условию данной задачи - время выполнения технологической операции больше установленной нормы).
Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.
В качестве критерия для сравнения выборочной средней с гипотетической генеральной средней нормальной совокупности, когда дисперсия генеральной совокупности известна, используется случайная величина U:
Его наблюдаемое значение (uнабл.) рассчитывается по формуле:
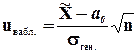. (8.4)
где 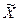- выборочная средняя;
а0 - числовое значение генеральной средней;
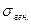- выборочное среднее квадратическое отклонение;
n - объем выборки.
Найдем наблюдаемое значение (uнабл.):
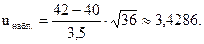
Так как конкурирующая гипотеза - правосторонняя, критическое значение uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства:
Ф0(uкр) = (1 - 2a) / 2.
По условию a = 0,01.
Отсюда:
Ф0(uкр) = (1 - 2·0,01) / 2 = 0,49.
По таблице функции Лапласа (приложение 2) найдем при каком uкр. Ф0(uкр) = 0,49.
F0(2,33) = 0,49.
Следовательно: uкр. = 2,33.
Заметим, что при левосторонней конкурирующей гипотезе Н1: a < 40 uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(uкр) = (1 - 2a) / 2 и присваивать ему "минус".
При двусторонней конкурирующей гипотезе Н1: a ¹ 40 uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(uкр) = (1 - a) / 2).
uнабл. > uкр, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей. По имеющимся хронометрическим данным с более чем 99%-ной надежностью можно утверждать, что среднее время выполнения этой операции превышает норму. Следовательно, жалобы работниц - обоснованны.
Область допустимых Критическая
значений область
U
0 uкр.= 2,33 uнабл.= 3,43
Рис. 8.5.
Наблюдаемое значение критерия попадает в критическую область, следовательно, нулевая гипотеза отвергается в пользу конкурирующей.
Ответ. По имеющимся хронометрическим данным на уровне значимости a = 0,01 можно утверждать, что среднее время выполнения этой операции превышает норму, жалобы работниц - обоснованны.
Пример 8.5 Экономический анализ производительности труда предприятий отрасли позволил выдвинуть гипотезу о наличии двух типов предприятий с различной средней величиной показателя производительности труда. Выборочное обследование 42-х предприятий первой группы дало следующие результаты: средняя производительность труда 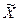составила 119 деталей. По данным выборочного обследования 35-и предприятий второй группы средняя производительность труда 
составила 107 деталей. Генеральные дисперсии известны: D(X) = 126,91 (дет.2); D(Y) = 136,1 (дет.2). Считая, что выборки извлечены из нормально распределенных генеральных совокупностей Х и Y, на уровне значимости 0,05 проверьте, случайно ли полученное различие средних показателей производительности труда в группах или же имеются два типа предприятий с различной средней величиной производительности труда.
Решение. Для решения данной задачи необходимо сравнить две средние нормально распределенных генеральных совокупностей, генеральные дисперсии которых известны (большие независимые выборки). В данной задаче речь идет о больших выборках, так как nx = 42 и ny = 35 больше 30. Выборки - независимые, так как из контекста задачи видно, что они извлечены из непересекающихся генеральных совокупностей.
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: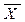 
= 
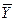- генеральные средние двух нормально распределенных совокупностей с известными дисперсиями равны (применительно к условию данной задачи - предприятия двух групп относятся к одному типу предприятий, - средняя производительность труда в двух группах - одинакова).
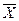Н1: 
¹ 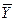- генеральные средние двух нормально распределенных совокупностей с известными дисперсиями не равны (применительно к условию данной задачи - предприятия двух групп относятся к разному типу предприятий, - средняя производительность труда в двух группах - неодинакова).
Выдвигаем двустороннюю конкурирующую гипотезу, так как из условия задачи не следует, что необходимо выяснить больше или меньше производительность труда в одной из групп предприятий по сравнению с другой.
Так как конкурирующая гипотеза - двусторонняя, то и критическая область - двусторонняя.
В качестве критерия для сравнения двух средних генеральных совокупностей, дисперсии которых известны (большие независимые выборки), используется случайная величина Z.
Его наблюдаемое значение (zнабл.) рассчитывается по формуле:
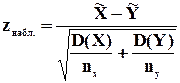, (8.5)
где 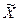- выборочная средняя для X;
- выборочная средняя для Y;
D(X) - генеральная дисперсия для X;
D(Y) - генеральная дисперсия для Y;
nx - объем выборки для X;
ny - объем выборки для Y.
Найдем наблюдаемое значение (zнабл.):
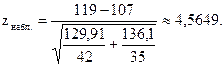
Так как конкурирующая гипотеза - двусторонняя, критическое значение (zкр.) следует находить по таблице функции Лапласа (приложение 2) из равенства:
Ф0(zкр) = (1 - a) / 2.
По условию a = 0,05.
Отсюда:
Ф0(zкр) = (1 - 0,05) / 2 = 0,475.
По таблице функции Лапласа (приложение 2) найдем при каком zкр. Ф0(zкр) = 0,475.
F0(1,96) = 0,475.
Учитывая, что конкурирующая гипотеза - двусторонняя, находим две критические точки:
zкр.(прав.) = 1,96; zкр.(лев.) = - 1,96.
Заметим, что при левосторонней конкурирующей гипотезе Н1: 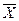< 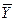zкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(zкр) = (1 - 2a) / 2 и присваивать ему "минус".
При правосторонней конкурирующей гипотезе Н1: 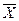> 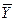zкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(zкр) = (1 - 2a) / 2).
zнабл. > zкр, следовательно, на данном уровне значимости нулевая гипотеза отвергается в пользу конкурирующей. На уровне значимости a = 0,05 можно утверждать, что полученное различие средних показателей производительности труда в группах - неслучайно, имеются два типа предприятий с различной средней величиной производительности труда.
 |
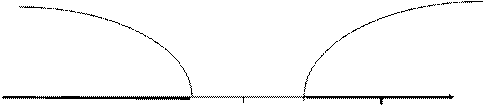Критическая Область допустимых Критическая
область значений область
Z
-zкр. = -1,96 0 zкр.= 1,96 zнабл.= 4,565
Рис. 8.6.
Наблюдаемое значение критерия попадает в критическую область, следовательно, нулевая гипотеза отвергается в пользу конкурирующей.
Ответ. На уровне значимости a = 0,05 можно утверждать, что полученное различие средних показателей производительности труда в группах - неслучайно, имеются два типа предприятий с различной средней величиной производительности труда.
Пример 8.6 Предполагается, что применение нового типа резца сократит время обработки некоторой детали. Хронометраж времени обработки 9 деталей, обработанных старым типом резцов, дал следующие результаты: среднее время обработки детали 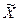составило 57 мин., исправленная выборочная дисперсия 
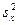= 186,2 (мин.2). Среднее время обработки 15 деталей, обработанных новым типом резца, по данным хронометражных измерений составило 52 мин., а исправленная выборочная дисперсия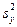 
= 166,4 (мин.2). На уровне значимости a = 0,01 ответьте на вопрос, позволило ли использование нового типа резцов сократить время обработки детали?
Решение. Для решения данной задачи необходимо сравнить две средние нормально распределенных генеральных совокупностей, генеральные дисперсии которых неизвестны, но предполагаются одинаковыми (малые независимые выборки). В данной задаче речь идет о малых выборках, так как nx = 9 и ny = 15 меньше 30. Выборки - независимые, так как из контекста задачи видно, что они извлечены из непересекающихся генеральных совокупностей.
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: 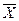= 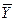- генеральные средние двух нормально распределенных совокупностей с неизвестными дисперсиями (но предполагаемыми одинаковыми) равны (применительно к условию данной задачи - среднее время, затрачиваемое на обработку детали резцами нового и старого типа - одинаково, т.е. использование нового типа резца не позволяет снизить время на обработку детали).
Н1: 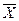> 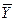- генеральная средняя для Х больше, чем генеральная средняя для Y (применительно к условию данной задачи - среднее время, затрачиваемое на обработку детали резцами старого типа больше, чем - нового, т.е. использование нового типа резца позволяет снизить время на обработку детали).
Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.
Приступать к проверке гипотезы о равенстве генеральных средних двух нормально распределенных совокупностей с неизвестными дисперсиями можно лишь в том случае, если генеральные дисперсии равны. В противном случае, данная задача в теории неразрешима.
Поэтому, прежде чем проверять эту гипотезу, проверим гипотезу о равенстве генеральных дисперсий нормальных совокупностей.
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: D(X) = D(Y) - генеральные дисперсии двух нормально распределенных совокупностей равны.
Н1: D(X) > D(Y) - генеральная дисперсия для X больше генеральной дисперсии для Y. Выдвигаем правостороннюю конкурирующую гипотезу, так как исправленная выборочная дисперсия для Х значительно больше, чем исправленная выборочная дисперсия для Y.
Так как конкурирующая гипотеза - правосторонняя, то и критическая область - правосторонняя.
В качестве критерия для сравнения двух дисперсий нормальных генеральных совокупностей используется случайная величина F - критерий Фишера-Снедекора.
Его наблюдаемое значение (fнабл.) рассчитывается по формуле:
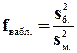, (8.6)
где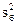 
- большая (по величине) исправленная выборочная дисперсия;
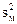- меньшая (по величине) исправленная выборочная дисперсия.
Найдем fнабл.:
.
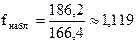Критическое значение (fкр.) следует находить по таблице распределения Фишера-Снедекора (приложение 6) по уровню значимости a и числу степеней свободы k1 и k2.
По условию a = 0,01; число степеней свободы найдем по формуле:
k1 = n1 - 1; k2 = n2 - 1,
где k1 - число степеней свободы большей (по величине) исправленной дисперсии;
k2 - число степеней свободы меньшей (по величине) исправленной дисперсии;
n1 - объем выборки большей (по величине) исправленной дисперсии;
n2 - объем выборки меньшей (по величине) исправленной дисперсии.
Найдем k1 и k2:
k1 = 10 - 1 = 8;
k2 = 15 - 1 = 14.
Определяем fкр. по уровню значимости a = 0,01 и числу степеней свободы k1=9 и k2=14:
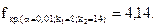
fнабл. < fкр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу о равенстве генеральных дисперсий нормальных совокупностей.
Следовательно, можно приступить к проверке гипотезы о равенстве генеральных средних двух нормально распределенных совокупностей.
В качестве критерия для проверки этой гипотезы, используется случайная величина t - критерий Стьюдента:
Его наблюдаемое значение (tнабл.) рассчитывается по формуле:
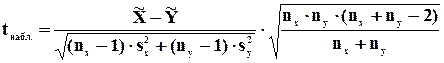, (8.7)
где 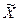- выборочная средняя для X;
- выборочная средняя для Y;
D(X) - генеральная дисперсия для X;
D(Y) - генеральная дисперсия для Y;
nx - объем выборки для X;
ny - объем выборки для Y.
Найдем tнабл.:
.
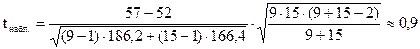Критическое значение (tкр.) следует находить по таблице распределения Стьюдента (приложение 5) по уровню значимости a и числу степеней свободы k.
По условию a = 0,01; число степеней свободы найдем по формуле:
k = nx + ny - 2,
где k - число степеней свободы;
nx - объем выборки для X;
ny - объем выборки для Y.
k = 9 + 15 - 2 = 22.
Найдем tкр. по уровню значимости a = 0,01 (для односторонней критической области) и числу степеней свободы k = 22:
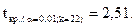
Заметим, что при левосторонней конкурирующей гипотезе 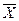< 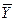tкр. следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для односторонней критической области) и числу степеней свободы k = nx + ny - 2 и присваивать ему "минус";
При двусторонней конкурирующей гипотезе 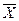¹ 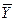tкр следует находить по таблицам распределения Стьюдента (приложение 5) по уровню значимости a (для двусторонней критической области) и числу степеней свободы k = nx + ny - 2).
tнабл. < tкр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу. По имеющимся хронометрическим данным на уровне значимости a = 0,01 нельзя отклонить гипотезу о том, что генеральные средние равны, т.е. среднее время, затрачиваемое на обработку детали старым и новым типом резцов отличается незначимо, расхождения между средними - случайны, использование нового типа резцов не позволяет снизить время обработки детали.
 |
Область допустимых Критическая
значений область
T
0 tнабл.= 0,9 tкр.= 2,51
Рис 8.7.
Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нулевую гипотезу нельзя отвергнуть.
Ответ. На уровне значимости a = 0,01 нельзя утверждать, что использование нового типа резцов позволило сократить время обработки детали.
Пример 8.7 Партия изделий принимается в том случае, если вероятность того, что изделие окажется соответствующим стандарту, составляет не менее 0,97. Среди случайно отобранных 200 изделий проверяемой партии оказалось 193 соответствующих стандарту. Можно ли на уровне значимости a = 0,02 принять партию?
Решение. Для решения данной задачи необходимо проверить гипотезу о том, что неизвестная генеральная доля точно равна определенному числу.
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: р = р0 = 0,97 - неизвестная генеральная доля р равна р0 (применительно к условию данной задачи - вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, равна 0,97; то есть партию изделий можно принять).
Н1: р < 0,97 - неизвестная вероятность р меньше гипотетической вероятности р0 (применительно к условию данной задачи - вероятность того, что деталь из проверяемой партии окажется соответствующей стандарту, меньше 0,97; то есть партию изделий нельзя принять).
Так как конкурирующая гипотеза - левосторонняя, то и критическая область - левосторонняя.
В качестве критерия для сравнения наблюдаемой относительной частоты с гипотетической вероятностью появления события используется случайная величина U:
Его наблюдаемое значение (uнабл.) рассчитывается по формуле:
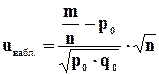, (8.8)
где m / n - относительная частота (частость) появления события;
р0 - гипотетическая вероятность появления события;
q0 - гипотетическая вероятность непоявления события;
n - объем выборки.
По условию: m = 193; n = 200; p0 = 0,97; q0 = 1 - p0 = 0,03; a = 0,02.
Найдем наблюдаемое значение (uнабл.):
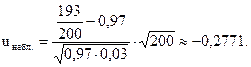
Так как конкурирующая гипотеза - левосторонняя, то критическое значение (uкр.) следует находить по таблице функции Лапласа (приложение 2) из равенства:
Ф0(uкр) = (1 - 2a) / 2.
По условию a = 0,02.
Отсюда:
Ф0(uкр) = (1 - 2 · 0,02) / 2 = 0,48.
По таблице функции Лапласа (приложение 2) найдем при каком uкр. Ф0(uкр) = 0,48.
F0(2,05) = 0,48.
Учитывая, что конкурирующая гипотеза - левосторонняя, критическому значению необходимо присвоить знак "минус".
Следовательно: uкр. = - 2,05.
Заметим, что при правосторонней конкурирующей гипотезе Н1: р > 0,97 uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(uкр) = (1 - 2a) / 2.
При двусторонней конкурирующей гипотезе Н1: p ¹ 0,97 uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(uкр) = (1 - a) / 2).
uнабл. > uкр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу. По имеющимся данным на уровне значимости a = 0,02 нельзя отклонить гипотезу о том, что вероятность того, что изделие окажется соответствующим стандарту, составляет 0,97. Следовательно, партию изделий принять можно.
 |
Критическая Область допустимых
область значений
U
-uкр.= - 2,05 uнабл. = - 0,28 0
Рис.8.8.
Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нет оснований отклонить нулевую гипотезу.
Ответ. На уровне значимости a = 0,02 партию изделий принять можно.
Пример 8.8 Два завода изготавливают однотипные детали. Для оценки их качества извлечены выборки из продукции этих заводов и получены следующие результаты:
| Завод №1 | Завод №2 | |
| Объем выборки | n1 | n2 |
| Число бракованных деталей | m1 | m2 |
На уровне значимости a = 0,025 определите, имеется ли существенное различие в качестве изготавливаемых этими заводами деталей?
Решение. Для решения данной задачи необходимо сравнить две вероятности биномиальных распределений.
Сформулируем нулевую и конкурирующую гипотезы согласно условию задачи.
Н0: р1 = р2 - вероятности появления события в двух генеральных совокупностях, имеющих биномиальное распределение, равны (применительно к условию данной задачи - вероятность того, что деталь изготовленная на первом заводе, окажется бракованной, равна вероятности того, что деталь изготовленная на втором заводе, окажется бракованной).
Н1: р1 ¹ р2 - вероятности появления события в двух генеральных совокупностях, имеющих биномиальное распределение, не равны (применительно к условию данной задачи - вероятность того, что деталь изготовленная на первом заводе, окажется бракованной, не равна вероятности того, что деталь изготовленная на втором заводе, окажется бракованной; заводы изготавливают детали разного качества). Так как по условию задачи не требуется проверить, на каком заводе качество изготавливаемых деталей выше, выдвигаем двустороннюю конкурирующую гипотезу.
Так как конкурирующая гипотеза - двусторонняя, то и критическая область - двусторонняя.
В качестве критерия для сравнения двух вероятностей биномиальных распределений используется случайная величина U:
Его наблюдаемое значение uнабл. рассчитывается по формуле:
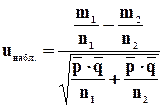, (8.9)
где m1 / n1 - относительная частота (частость) появления события в первой выборке;
m2 / n2 - относительная частота (частость) появления события во второй выборке;
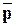- средняя частость появления события;
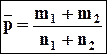
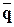- средняя частость непоявления события;
;
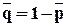n1 - объем первой выборки;
n2 - объем второй выборки.
По условию: m1 = 20; n1 = 200; m2 = 15; n2 = 300; a = 0,025.
Найдем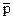 
- среднюю частость появления события:
.
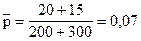Найдем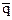 
- среднюю частость непоявления события:
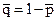= 1 - 0,07 = 0,93.
Найдем uнабл.:
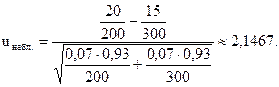
Так как конкурирующая гипотеза - двусторонняя, критическое значение (uкр.) следует находить по таблице функции Лапласа (приложение 2) из равенства:
Ф0(uкр) = (1 - a) / 2.
По условию a = 0,025.
Отсюда:
Ф0(uкр) = (1 - 0,025) / 2 = 0,4875.
По таблице функции Лапласа (приложение 2) найдем при каком uкр. Ф0(uкр) = 0,4875.
F0(2,24) = 0,4875.
Учитывая, что конкурирующая гипотеза - двусторонняя, находим две критические точки:
uкр.(прав.) = 2,24; uкр.(лев.) = - 2,24.
Заметим, что при правосторонней конкурирующей гипотезе Н1: р1 > р2 uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(uкр) = (1 - 2a) / 2.
При левосторонней конкурирующей гипотезе Н1: р1 < р2 uкр. следует находить по таблице функции Лапласа (приложение 2) из равенства Ф0(uкр) = (1 - 2a) / 2 и присваивать ему знак "минус").
-uкр. < uнабл. < uкр, следовательно, на данном уровне значимости нет оснований отвергнуть нулевую гипотезу. По имеющимся данным на уровне значимости a = 0,025 нет оснований отклонить нулевую гипотезу. Следовательно, заводы изготавливают детали одинакового качества.
 |
Критическая Область допустимых Критическая
область значений область
U
-uкр. = -2,24 uнабл.= 2,15 uкр.= 2,24
Рис.8.9.
Наблюдаемое значение критерия попадает в область допустимых значений, следовательно, нет оснований отклонить нулевую гипотезу.
Ответ. Нет оснований отклонить нулевую гипотезу, то есть имеющееся различие в качестве изготавливаемых этими заводами деталей - случайно, незначимо.
