Полная энергия электрона в атоме. Свет. Излучение и поглощение фотонов

Полная энергия электрона в атоме не изменяется, пока он находится на своей орбитали. Поэтому для каждой орбитали любого атома можно указать точную величину полной энергии находящегося на ней электрона (рис. 73). Промежуточные значения энергии для электрона "запрещены". Например, в атоме кислорода энергия электрона может соответствовать орбитали 1s или2s, но не может быть промежуточной между ними.

Электроны могут захватывать частицы света - фотоны. В результате захвата фотона энергия электрона увеличивается, и он "перескакивает" на другую орбиталь, соответствующую новому значению его полной энергии. Разумеется, электрон может поглотить не любой фотон, а лишь такой, энергия которого в сумме с энергией этого электрона составляет "разрешенную" величину, то есть позволяет "перепрыгнуть" на определенную орбиталь, занятую в этот момент не более чем одним другим электроном. Совершив такой "прыжок", электрон недолгое время (порядка триллионной доли секунды) находится на новой орбитали, а затем "проваливается" обратно, излучая в случайном направлении точно такой же фотон, какой захватил раньше. Точнее говоря, возможен и "ступенчатый" спуск на исходную орбиталь через одну или несколько промежуточных, при этом суммарная энергия излученных фотонов в точности равна энергии поглощенного фотона.

36. В 1924 г. де Бройль выдвинул гипотезу (предположение), что дуализм (двойственность) не являются особенностью одних только оптических явлений (см. лекцию 8), а имеет универсальное значение, т.е. де Бройль выдвинул гипотезу о всеобщности корпускулярно-волнового дуализма. Согласно де Бройлю каждой частице, независимо от ее природы, следует поставить в соответствии волну, длина которой l связана с импульсом частицы соотношением (формула де Бройля) 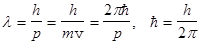, (1)

а частота

v=E/h или w=2pv=E / 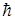, (2)

т.е. определяется энергией Е частицы.

Найдем длину волны де Бройля, соответствующую движущемуся электрону. Кинетическая энергия, приобретенная электроном в ускоряющем поле равна

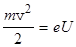(3)

и скорость

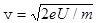(4)

Из (1) и (4) следует (учитывая, что е= 1.6×10^-19 Кл, m= 9.1×10^-31 кг, напряжение U выражается в вольтах)

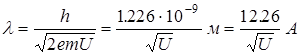. (5)

В обычных электронных приборах используют напряжение 1¸10⁴ В. Соответствующие длины волн летящих электронов составляют 10¸0.1 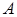, т.е. изменяются в диапазоне длин волн обычных рентгеновских лучей (см. параграф 2.5).

По гипотезе де Бройля не только фотоны [см.(8.4)], но и все «обыкновенные частицы» (электроны, протоны, нейтроны и др.) обладают волновыми свойствами, которые, в частности, должны проявляться в явлениях интерференции, дифракции.

Гипотеза де Бройля вскоре была подтверждена экспериментально. Девиссон и Джермер в 1927 г. наблюдали дифракцию электронов на монокристалле никеля. Узкий пучок электронов направлялся на поверхность монокристалла никеля. Отраженные электроны улавливались цилиндрическим электродом (см. рис.1), присоединенным к гальванометру. Интенсивность отраженного пучка оценивалась по силе тока, текущего через гальванометр. Ожидали получить дифракционную картину, аналогичную картине возникающей при дифракции рентгеновских лучей на том же кристалле, поскольку длина волны де Бройля для электронов изменялась в диапазоне длин волн рентгеновских лучей. Ожидание подтвердилось.

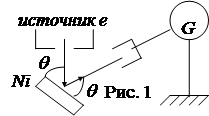Согласно формуле Вульфа-Брегга [см. лекции 4, 5 формула (13)] условие дифракционного максимума имеет вид

2dsinq=ml,(6)

где d – расстояние между атомными плоскостями, q – угол скольжения, m= 1, 2, 3 ...

Для никеля d=2.03 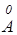, опыт проводился при q = 80°;с учетом этого и формулы (5) из (6) следует

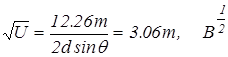. (7)

Все это подтвердилось на опыте, особенно при больших значениях m (m = 6, 7, 8). При определенных дискретных напряжениях, определяемых согласно (7), гальванометр фиксировал максимальный ток (рис. 2).

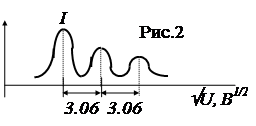Итак, опыт Девиссона-Джермера подтвердил гипотезу де Бройля – движущиеся электроны ведут себя как волны. Позднее были поставлены другие опыты, подтверждающие волновые свойства микромира.

Заметим, что волны де Бройля имеют специфическую квантовую природу, не имеющую аналогии с волнами в классической физике, т.е. они «не похожи ни на что из того, что вам когда-нибудь приходилось видеть» (Фейнман).

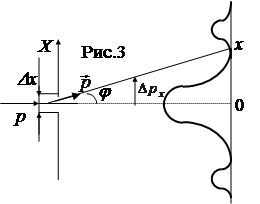В классической физике «понять» означало составить себе наглядный образ объекта или процесса. Квантовую физику нельзя понять в таком смысле слова и поэтому следует отказаться от попыток строить наглядные модели поведения квантовых объектов.

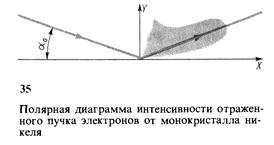
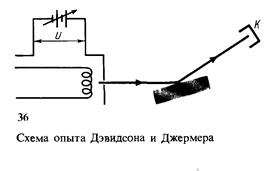
Опыты Дэвидсона и Джермера.

Дэвидсон и Джермер наблюдали отражение электронного пучка от поверхности кристалла. В первом опыте на монокристалл никеля направляли электроны с энергией в несколько десятков электрон-вольт. Затем, изменяя угол падения электронов на поверхность кристалла, фиксировали изменение интенсивности отраженного пучка. Зависимость интенсивности отраженного

пучка от угла скольжения а показана на рис. 35. На полярной диаграмме отчетливо виден максимум интенсивности отражения при угле a₀.

Во втором опыте при фиксированном угле падения электронного пучка на кристалл измерялась интенсивность отраженного пучка в зависимости от энергии Интенсивность пучка отраженных электронов измерялась по силе тока от коллектора электронов К (рис. 36).

Результаты эксперимента показаны на рис. 37.

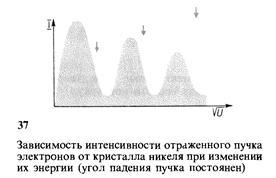
Результаты опытов Дэвидсона и Джермера получили объяснение (1927) как проявление волновой природы электронов и дали количественное подтверждение справедливости формул де Бройля.

В теоретическом плане анализ дифракции электронных волн полностью совпадает с дифракцией рентгеновских лучей. Расчет длины волны по дифракционной картине совпадает с длиной волны предсказанной Луи-де- Бройля.

Опыт Бибермана – Сушкина - Фабриканта.

Определение координат и импульса микрочастицы

Во второй половине XX столетия немалые усилия ученых, работающих в

области физики микрочастиц, были посвящены возможности

экспериментального подтверждения одного из основных положений квантовой

механики – принципа неопределенности Гейзенберга. Для этого было

необходимо осуществить эксперименты, которые позволяли бы наглядно

установить координаты и импульс микрочастиц. Серьезный успех при решении

этой фундаментальной задачи имел опыт, осуществленный советскими

физиками Л. Биберманом, Н. Сушкиным и В. Фабрикантом. Принципиальная

схема устройства, позволяющего прямым путем определять положение

электрона, представлена на рис. 22. На экран со щелью AB шириной ∆x,

Рис. 22. Определение положения электрона с помощью экрана со щелью.

который можно рассматривать как соответствующую диафрагму, слева падает

электрон в направлении, перпендикулярном к плоскости этой диафрагмы.

Пусть ось OX направлена параллельно диафрагме, а ось OY расположена

перпендикулярно к ней. Если на флуоресцирующем экране, расположенном

справа от диафрагмы, по характерным сцинтилляциям удается обнаружить

электрон, то можно утверждать, что он прошел через щель AB. В этом случае

«место электрона» в момент прохождения через щель можно определить как

положение щели относительно других частей прибора, поскольку положение

щели в диафрагме будет фиксированным относительно данной системы

отсчета. Следовательно, положение электрона в момент прохождения через

щель будет известно с погрешностью ∆x, которая равна ширине щели. Сужая

щель, можно повышать точность определения положения электрона, причем

предела для повышения точности теоретически не существует.

На первый взгляд может показаться, что и импульс электрона можно

установить со всей определенностью. Если принять во внимание, что

направление движения электрона слева от диафрагмы перпендикулярно ее

плоскости (рис. 22), то x – составляющая импульса слева от экрана равна нулю,

а y – составляющая равна p. Таким образом, в такой ситуации имеет импульс

электрона определенное значение. Однако при прохождении через щель

плоская волна де Бройля, описывающая движение свободного электрона,

испытывает дифракцию. Если вместо одного электрона в направлении оси OY

через диафрагму будет двигаться параллельный поток микрочастиц, тогда на

фотопластине или флуоресцирующем экране появляется дифракционная

картина, состоящая из размытого главного максимума и более слабых по

интенсивности максимумов более высоких порядков, расположенных

симметрично относительно оси OY (рис. 22). Характер дифракционной картины

свидетельствует, что после прохождения через щель большинство электронов

продолжает двигаться в первоначальном направлении. Тем не менее,

появляются электроны, которые изменяют свое направление и попадают в

различные точки фотопластинки с изменяющейся вероятностью. Безусловно,

что всей очевидностью такая дифракционная картина возникает тогда, когда

через щель одновременно проходит большое число электронов.

Советские физики Л. Биберман, Н. Сушкин и В. Фабрикант

экспериментально доказали, что при прохождении через дифрагирующую

систему отдельных электронов поодиночке (такие электроны ведут себя

абсолютно независимо друг от друга) через относительно большие промежутки

времени при достаточной продолжительности опыта возникает дифракционная

картина, в точности совпадающая с той, которую дают потоки с

интенсивностью в десятки миллионов электронов. В этом опыте промежуток

времени между двумя последовательными прохождениями электронов через

дифрагирующую систему примерно в 30000 раз превышал длительность

прохождения всего прибора одним отдельным электроном. Это

свидетельствует о том, что изменение направления полета электрона, ведущее к

возникновению характерной дифракционной картины, происходит при

индивидуальном прохождении электронов через дифрагирующую систему.

В этом опыте установка позволяет измерить положение микрочастицы с

неопределенностью ∆x, которую в принципе можно сделать сколь угодно

малой величиной. Однако при жестко закрепленной диафрагме невозможно

учесть отдачу, испытываемую диафрагмой при прохождении электрона.

Поэтому добавочный импульс, приобретаемый частицей, остается в известных

пределах ∆px неопределенным. Можно доказать, что неопределенности ∆x и

∆px связаны соотношением ∆x⋅∆px ≥ 2πħ.

Из рис. 22 видно, что

2π

∆px = p sin α = sin α (11-1)

λ

Если учитывать попадания электрона на фотопластину в пределах только

главного дифракционного максимума, угол α будет углом между осью OY и

направлением к первому дифракционному минимуму. Положение этого

минимума определяется условием, чтобы разность хода волн,

дифрагированных от верхнего и нижнего краев диафрагмы, равнялась длине

волны λ. Отсюда получаем (см. рис. 22)

∆x sin α = λ (11-2)

или

λ

∆x = (11-2а)

sin α

Перемножая левые и правые части соотношений (11-1) и (11-2а), получаем

2π λ

∆x ⋅ ∆px = sin α ⋅ = 2π (11-3)

λ sin α

Если учесть побочные дифракционные максимумы, то вместо условия (11-3)

придется записать

∆x ⋅ ∆px = n2π (11-4)

Следовательно, в общем виде

∆x ⋅ ∆px ≥ 2π (11-5)

Соотношение (11-5) отражает принцип неопределенности Гейзенберга.

Таким образом, опыт Биберман - Сушкина – Фабриканта является

экспериментальным подтверждением одного из основных положений

квантовой механики – принципа неопределенности Гейзенберга.

37. Волновая функция и ее физический смысл.

Из содержания предыдущих двух параграфов следует, что с микрочастицей сопоставляют волновой процесс, который соответствует ее движению, поэтому состояние частицы в квантовой механике описывают волновой функцией, которая зависит от координат и времени y(x,y,z,t). Конкретный вид y -функции определяется состоянием частицы, характером действующих на нее сил. Если силовое поле, действующее на частицу, является стационарным, т.е. не завися­щим от времени, то y -функцию можно представить в виде произведения двух сомножителей, один из которых зависит от времени, а другой – от координат:

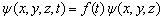(3.1)

В дальнейшем будем рассматривать только стационарные состояния. y-функция является вероятностной характеристикой состояния частицы. Чтобы пояснить это, мысленно выделим достаточно малый объем 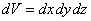, в пределах которого значения y-функции будем считать одинаковыми. Тогда вероятность нахождения dW частицы в данном объ­еме пропорциональна ему и зависит от квадрата модуля y-функции (квадрата модуля амплитуды волн де Бройля):

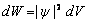(3.2)

Отсюда следует физический смысл волновой функции:

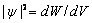. (3.3)

Квадрат модуля волновой функции имеет смысл плотности вероят­ности, т.е. определяет вероятность нахождения частицы в единичном объеме в окрестности точки с координатами х, у, z.

Интегрируя выражение (3.2) по объему, определяем вероятность нахождения частицы в этом объеме в условиях стационарного поля:

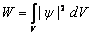(3.4)

Если известно, что частица находится в пределах объема V, то инте­грал выражения (3.4), взятый по объему V, должен быть равен единице:

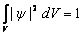(3.5)

– условие нормировки y-функции.

Чтобы волновая функция являлась объективной характеристикой со­стояния микрочастиц, она должна быть конечной, однозначной, непре­рывной, так как вероятность не может быть больше единицы, не может быть неоднозначной величиной и не может изменяться скачками. Таким образом, состояние микрочастицы полностью определяется волновой функцией. Частица может быть обнаружена в любой точке пространства, в которой волновая функция отлична от нуля.