Тема 2. Численные методы решения систем линейных уравнений

Содержание лекции

Содержание лабораторной работы

Точные и приближенные методы решения систем линейных уравнений. Полные метрические пространства. Теорема о сжимающих отображениях в полном метрическом пространстве и ее следствия. Применение теоремы о сжимающих отображениях при решении системы линейных уравнений: простые итерации, метод Зейделя. Погрешности округления при практической реализации итерационного процесса. Число операций при решении системы линейных уравнений методом Гаусса. Оценка погрешности решения системы линейных алгебраических уравнений. Понятие об обусловленности. Метод прогонки, трехдиагональная матрица. Релаксация.

Решение систем линейных уравнений. Метод Гаусса. Метод простой итерации/ Оценка погрешности решения системы линейных алгебраических уравнений. Понятие об обусловленности. Метод прогонки, трехдиагональная матрица. Релаксация.

Задание

Дана система трех линейных уравнений с тремя неизвестными:

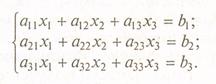
1. Решите систему методом Гаусса:

а) используя «ручную» схему единственного деления, двумя
способами: без перестановки строк; с перестановкой строк; расчеты выполняйте с тремя знаками после запятой (с применением
калькулятора); подставьте найденные решения в исходную систему, вычислите невязки и сравните полученные решения; выбрав
ведущие элементы схемы единственного деления, найдите значение определителя системы;

б) с помощью программы для ЭВМ с пооперационным учетом ошибок.

2. Решите систему методом простой итерации с точностью е = 10~4 с помощью программы для ЭВМ.

Исполнение: применить а) метод Гаусса; б) метод простой итерации используя любой инструментальный пакет.

Лабораторная установка: Персональный компьютер с ОС Windows, MS Office, MathCad.

Оценка: Сопоставление полученных результатов, решаемых различными методами.

Время выполнения работы: 4 часа.

Методические указания

Табличный процессор Excel

В табличном процессоре Excel для решения систем уравнений есть два варианта: реализация алгоритмов в электронной таблице с помощью основных средств табличного процессора и использование специальных средств.

Первый вариант проиллюстрирован на примере системы уравнений

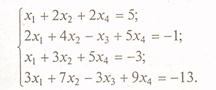
На рис. приведены идентичные тексты в Excel, но один — в режиме отображения формул, а другой — значений. Из них прекрасно видно устройство алгоритма.

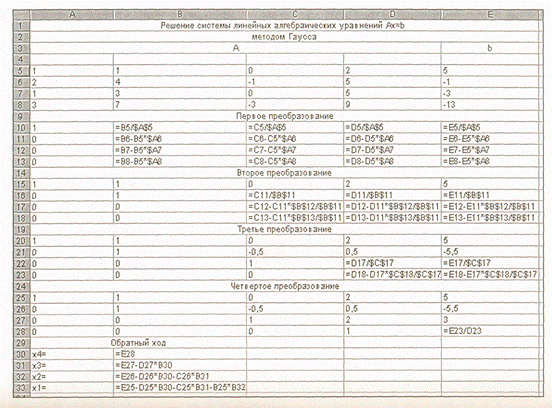
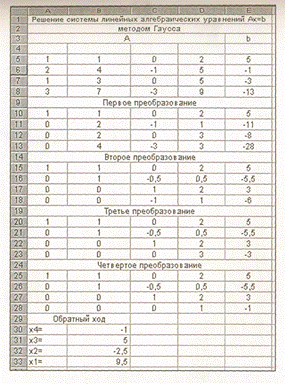
Рис.1

Второй вариант не столь очевиден. Среди встроенных в Excel математических программ программы решения систем уравнений, строго говоря, нет.

Неточно так же, как для решения уравнений было использовано средство Подбор параметра, для решения систем может быть использовано средство, предназначенное совсем для другой цели (для решения задач оптимизации).

Это средство - Поиск решения. Поясним его использование и приведем примеры применения.

Средство Поиск решения активируется в меню Сервис (если это средство не установлено, то это необходимо сделать).

Предварительно проводят следующую подготовительную работу.

Отводят для каждой переменной по ячейке.

Вводят формулы для вычисления правых частей уравнений
системы (по одной формуле в ячейку).

После этого запускают Поиск решения. Возможный вид экрана для подготовки к решению той же системы, что и выше, приведен на рис. На этом рисунке под переменные отведены ячейки A2:D2, под формулы — ячейки А4, А6, А8 и А10. Какие именно числовые значения переменных будут введены в ячейки A2:D2, при решении системы линейных уравнений значения не имеет (итерационная процедура, заложенная в Поиск решения, стартует с этих значений).

Еще один элемент в таблице — целевая функция. Она в данном случае особой роли не играет, но какую-нибудь формулу ввести необходимо, иначе Поиск решения работать не может (напомним, что эта программа нацелена на другой класс задач). Точно так же неважно, как установлен флажок: «максимальному значению» или «минимальному значению».

Теперь необходимо ввести то, что в форме на рис. 2 именуется ограничениями. Щелкнув по кнопке Добавить, получают другую форму (рис.3).

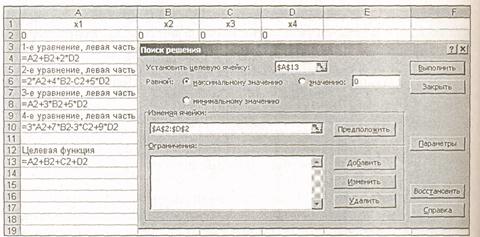
Рис2.

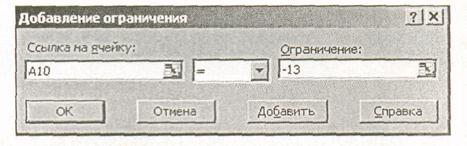
Рис3.

В форму, изображенную на рис. 3. надо ввести четыре условия (по числу уравнений системы). На рисунке отражено последнее условие. Ссылка на ячейку А10 обусловлена тем, что в ней -формула для левой части 4-го уравнения, знак '=' выбран из меню, число (-13) введено с клавиатуры (правая часть 4-го уравнения). После ввода последнего ограничения нажимают кнопку ОК и возвращаются в основную форму Поиск решения. Щелкнув по кнопке Выполнить, получают результат (рис. 4).

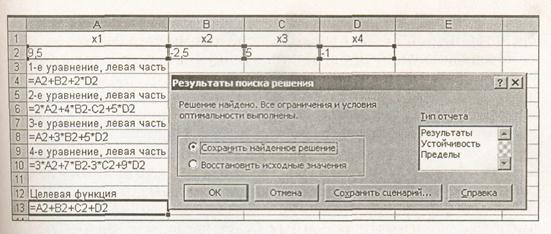
Рис4.

Каким методом это решение получено, можно узнать, щелкнув по кнопке Параметры (см. рис. 2). Там, в частности, есть знакомый нам метод Ньютона (наверняка сильно видоизмененный, поскольку применяется на самом деле к решению гораздо более сложной задачи).

Поиск решения можно попытаться применить и к решению систем нелинейных уравнений. В этом случае выбор начального приближения очень важен, в зависимости от него решение может быть получено или не получено и могут быть получены разные решения.

Система Maple

Решение систем линейных уравнений (см. пример 1) матричным методом в Maple (рис. 5) реализуют два класса функций:

1) функции для задания векторов и матриц:

matrix(n,m,lisf) — возвращает матрицу размерности п х т с заданными списком элементами, которые перечисляются через запятую построчно (элементы каждой строки заключается в квадратные скобки, а строки разделяются запятыми);

vector(n,lisf) — возвращает вектор с п элементами, заданными списком;

2) функции для работы с векторами и матрицами:

multiply(A,B) -- возвращает произведение матриц А и В;

inverse(A) — возвращает матрицу, обратную А.

Решение представляет собой список элементов вектора х.

Этот же метод используется функцией linsolve(A,B), аргументами которой являются матрица А и матрица (или вектор) В (рис. 6) для решения матричного уравнения вида Ах = В.

Рис5.

Рис6.

Для решения систем линейных и нелинейных уравнений может быть применена функция solve({eql,eq2,..,},{varl,var2,...}), где eq — уравнение, var — переменная, по которой ищется решение. Уравнения и список переменных задаются в виде множества, поэтому результат будет получен также в виде множества в аналитическом виде (символьной форме).

Краткая теория метода итераций

Рассмотрим систему линейных алгебраических уравнений

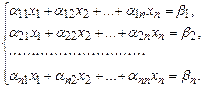(1)

Систему уравнений можно записать в матричном виде

Рx=b, (2)

где

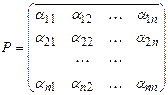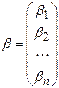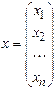, , . (3)

В выражении (2) матрица Р и вектор b заданы, вектор x является искомым решением задачи.

Если все диагональные коэффициенты 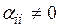(i=1,2,…,n), то систему (1) можно представить в так называемом приведенном виде:

(4)

где

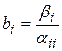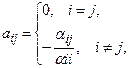, i,j=1, 2, …, n. (4')

Введем обозначение

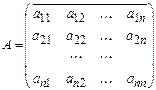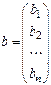
и перепишем систему (4) в виде матричного уравнения

x=Ax+b. (5)

Метод итераций заключается в нахождении последовательных приближений решения x. Возьмем в качестве начального приближения x0 вектор b и подставим его в правую часть уравнения (5), получим вектор x1. Продолжая аналогичные вычисления, придем к векторной последовательности приближений:

x1=Ax0+b,

x2=Ax1+b,

……..

xk+1=Axk+b,

………

Процесс вычисления последовательных приближений продолжают до тех пор, пока полученные значения на двух последовательных шагах существенно отличаются друг от друга. В таком случае условие прекращения вычислений можно записать так

d=max{|x ik+1- x ik|}<e, i=1,2,..n.

Для того чтобы описанным методом можно было найти решение системы уравнений (1) матрица Р должна удовлетворять достаточному условию сходимости метода итераций. Матрица Р должна быть с диагональным преобладанием, т.е. в каждой стоке элемент, стоящий на главной диагонали, по модулю должен быть больше суммы модулей остальных элементов строки. В случае, когда матрица не имеет диагонального преобладания, необходимо провести преобразования.

Теорема. Если матрица P является симметричной положительно-определенной матрицей, то итерационный процесс (6) сходится к решению уравнения (5) при произвольном x0.

Замечание. Для того, чтобы преобразовать исходное уравнение к виду с симметричной положительно-определенной матрицей, необходимо умножить уравнение (2) на транспонированную матрицу PT.

Контрольные вопросы и задания

1) Запустить программу Excel, открыть рабочую книгу лабораторных работ. Создать в ней новый лист, дать ему имя «Мет.итераций».

2) Оформить рабочий лист.

Значения коэффициентов матрицы P и вектора b взять по своему варианту, таблица 4 Приложения.

3) Привести систему к виду (4).

4) Умножить матрицу P и вектор b на транспонированную матрицу P^T. Преобразовать коэффициенты по формулам (4'). В формулах вычисления коэффициентов a_ij и b_i (i ¹ j) использовать абсолютную адресацию. Коэффициенты a_ii задать равными нулю.

5) Для начала итерационного процесса задать значение вектора x⁰ равным b. Ввести формулы для вычисления x^k⁺¹ и d. При ссылке на матрицу А можно использовать абсолютные адреса, для вектора b удобно ячейкам с элементами вектора присвоить имена и в формулах ссылаться на них:

	=H24+v_b1
x^k+1=	=H25+v_b2
	=H26+v_b3
	=H27+v_b4

Ячейкам со значениями величин e и d также следует присвоить имена для использования в формулах.

Для переноса значений x^k⁺¹ на следующий шаг в ячейки x^k необходимо использовать функцию ЕСЛИ с условием e< d.

6) Копировать ячейки, относящиеся к одному шагу итераций до тех пор, пока e< d.

7) Выделить в отдельные ячейки окончательный ответ с 3 десятичными знаками. Сравнить полученные значения с точным решением системы уравнений и решением, полученным выше.

Таблица 4

№ варианта	Система линейных алгебраических уравнений	корни системы	№ варианта	Система линейных алгебраических уравнений	корни системы
1.		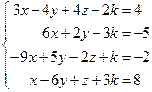	2.		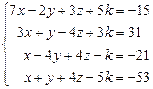-2 -4 -8
3.		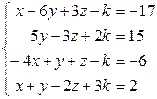-1	4.		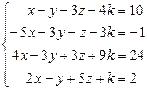-5 -2
5.		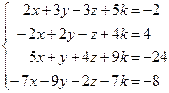-2 -2	6.		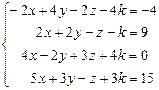-2 -4 -1
7.		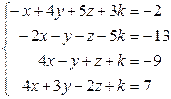-2 -4	8.		-3 -1 -5 -2
9.		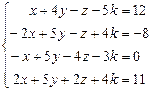-1	10.		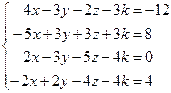-1 -5
11.		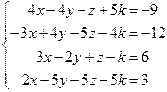-1 -2 -2	12.		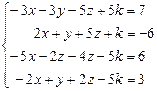-3 -1
13.		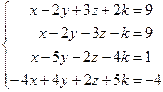-2 -2	14.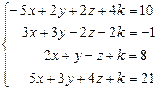
15.		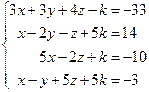-3 -5 -2	16.		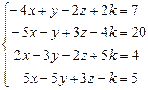-3 -3
17.		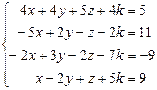-2 -3	18.		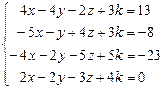-2 -1
19.		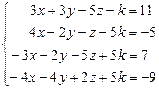-2 -2 -1	20.		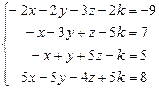-2 -3
21.		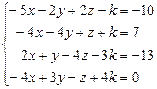-3 -1	22.		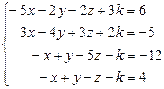-5 -2 -5
23.		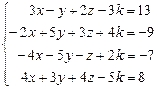-2	24.		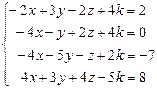-3 -3
25.		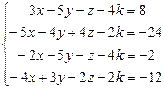-2 -4	26.		-2 -2 -1 -1