При изучении любого типа задач оптимизации важное место занимает вопрос об условиях оптимальности или, как говорят, условиях экстремума. Различают необходимое условие оптимальности, т.е. условия, которым должна удовлетворять точка, являющаяся решением задачи, и достаточные условия оптимальности, т.е. условия, из которых следует, что данная точка является решением задачи.
Замечания:
1. Если функция обладает свойством унимодальности, то локальный минимум автоматически является глобальным минимумом.
2. Если функция не является унимодальной, то возможно наличие нескольких локальных оптимумов, при этом глобальный минимум можно определить путём нахождения всех локальных оптимумов и выборе наименьшего из них.
Теорема 4.1. (необходимое условие минимума первого порядка): Пусть функция ¦ дифференцируема в точке 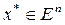 . Если
. Если 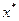 – локальное решение задачи (4.1), то
– локальное решение задачи (4.1), то
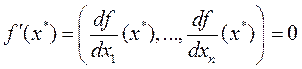 (4.5)
(4.5)
или
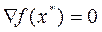 ,
,
где 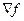 – градиент функции.
– градиент функции.
Точка х *, удовлетворяющая условию (4.5), называется стационарной точкой функции ¦ или задачи (4.1). Ясно, что стационарная точка не обязана быть решением, т.е. (4.5) не является достаточным условием оптимальности. Такие точки являются подозрительными на оптимальные.
Пример 4.1. Рассмотрим, например, функцию f (x) = x 3 (рис. 4.4). Эта функция удовлетворяет необходимому условию оптимальности, однако, не имеет ни максимума, ни минимума при х * = 0, т.е. 
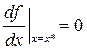 и точка х * – стационарная точка.
и точка х * – стационарная точка.
Если стационарная точка не соответствует локальному оптимуму (минимуму или максимуму), то она является точкой перегиба или седловой точкой. Для тогочтобы провести различия между случаями, когдастационарная точка соответствует локальному минимуму, локальному максимуму или является точкой перегиба, необходимо построить достаточные условия оптимальности.
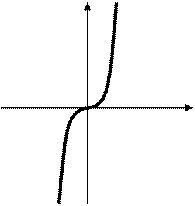
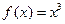
x* x
Рис. 4.6. График функции, имеющей точку перегиба
Теорема 4.2. (необходимое условие минимума второго порядка): Пусть функция ¦ дважды дифференцируема в точке 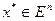 . Если х * – локальное решение задачи (4.1), то матрица
. Если х * – локальное решение задачи (4.1), то матрица 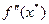 неотрицательно определена, т.е.
неотрицательно определена, т.е.
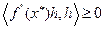
 h
h 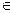 En, (4.6)
En, (4.6)
где 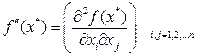 – гессиан функции ¦ в точке
– гессиан функции ¦ в точке 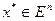 .
.
Достаточное условие локальной оптимальности содержит характерное усиление требований на матрицу 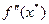 .
.
Теорема 4.3. (достаточное условие минимума второго порядка): Пусть функция ¦ дважды дифференцируема в точке 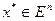 . Предположим, что
. Предположим, что 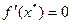 , а матрица
, а матрица 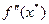 положительно определена, т.е.
положительно определена, т.е.
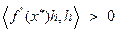 ,
, 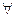 h
h 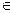 En, h ≠ 0. (4.7)
En, h ≠ 0. (4.7)
Тогда х * – строгое локальное решение задачи (4.1). Для функции числового аргумента (n = 1) условия (4.6) и (4.7) означают, что вторая производная 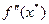 как скалярная величина не отрицательна и положительна соответственно.
как скалярная величина не отрицательна и положительна соответственно.
Итак, для функции ¦ числового аргумента не является гарантией наличие оптиума при выполнении условий 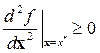 − минимум;
− минимум; 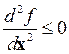 − максимум.
− максимум.
Для того чтобы стационарная точка была точкой экстремума, необходимо выполнение достаточных условий локального экстремума. Достаточным условием является следующая теорема.
Теорема 4.4. Пусть в точке х * первые (n −1) производные функции обращаются в нуль, а производная n -го порядка отлична от нуля:
1) Если n − нечетное, то х * – точка перегиба;
2) Если n − четное, то х * – точка локального оптимума.
Кроме того:
а) если эта производная положительная, то х * – точка локального минимума;
б) если эта производная отрицательна, то х * – точка локального максимума.
Для того чтобы применить эту теорему 4.4 к функции f (x) = x 3 (пример 4.1), вычислим:
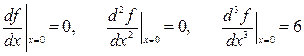 .
.
Так как порядок первой отличной от нуля производной равен 3 (нечётное число), точка х = 0 является точкой перегиба.
Пример 4.2. Рассмотреть функцию, определенную на всей действительной оси и определить особые точки:

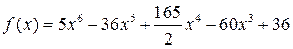 .
.
 2015-02-04
2015-02-04 2806
2806
