Метод перебора

Численные методы решения задач одномерной оптимизации

Задача оптимизации, в которой целевая функция задана функцией одной переменной, относится к наиболее простому типу оптимизационных задач. Это связано не только с тем, что именно такие задачи обычно решаются в инженерной практике, но и с тем, что одномерные методы оптимизации часто используются для анализа подзадач, которые возникают при реализации итеративных процедур, ориентированных на решение многомерных задач оптимизации.

Для решения задачи минимизации функции ¦(x) на отрезке [ a; b ] на практике, как правило, применяют приближенные методы. Они позволяют найти решение этой задачи с необходимой точностью в результате определения конечного числа значений функции ¦(x) и ее производных в некоторых точках отрезка [ a; b ]. Методы, использующие только значения функции и не требующие вычисления ее производных, называются прямыми методами минимизации.

Прямые методы

Большим достоинством прямых методов является то, что от целевой функции не требуется дифференцируемости и, более того, она может быть не задана в аналитическом виде. Единственное, на чем основаны алгоритмы прямых методов оптимизации, это возможность определения значений ¦(x) в заданных точках.

Рассмотрим наиболее распространенные на практике прямые методы поиска точки минимума. Самым слабым требованием на функцию ¦(x), позволяющим использовать эти методы, является ее унимодальность. Поэтому далее будем считать функцию ¦(x) унимодальной на отрезке [ a; b ].

Метод перебора

Метод перебора (пассивная стратегия поиска) является простейшим из прямых методов оптимизации.

Пусть

¦(x) Î Q [ a; b ],

где Q [ a; b ] – множество унимодальных функций на отрезке [ a; b ]. Требуется найти какую–либо из точек минимума x функции ¦(x) на отрезке [ a; b ] с абсолютной погрешностью e >. Разобьем [ a; b ] на n равных частей точками деления

x 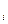= a + i 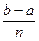, i = 0, 1, 2,…, n,

где n ³ .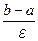

Вычислив значения ¦(x) в этих точках, путем сравнения найдем точку x , для которой

¦(x 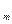) = min¦(x 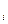), 0 £ i £ n.

Далее полагаем x 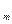» x , ¦ » ¦(x 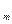). При этом максимальная погрешность e 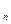определения точки x равна e 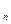= (b - a)/ n.

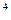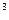Пример 5.1. Найти минимальное значение ¦ и точку минимума x функции ¦(x) = x + 8 x - 6 x 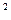- 72 x на отрезке [1,5; 2,0]. Точку x найти с погрешностью e = 0,05.

¦(x)Î Q [1,5; 2,0], так как ¦¢¢(x) = 12 x 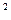+ 48 x – 12 > 0 при x Î [1,5; 2].

Выбрав n = 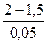= 10, вычислим значения ¦(x ), x 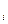= 1,5 + i 0,05, i = 0,1,…,10, поместив их в таблицу 5.1.

хi	1,50	1,55	1,60	1,65	1,70	1,75	1,80	1,85	1,90	1,95	2,00
¦(x 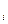)	-89,4	-90,2	-91,2	-91,8	-92,08	-92,12	-91,9	-91,4	-90,5	-89,4	-88,0

Таблица 5.1

Значения функции f (x_i)

Из таблицы 5.1 находим x » 1,75, ¦ » -92,12.