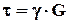
где G – модуль сдвига или модуль упругости II-го рода
Упругие постоянные материала связаны зависимостью:
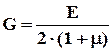 где m - коэффициент Пуассона.
где m - коэффициент Пуассона.
Он равен отношению поперечной деформации 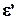 бруса к продольной деформации
бруса к продольной деформации 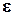 , взятого по модулю.
, взятого по модулю.
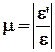
m стали = 0,25 –0,35
5. Основные гипотезы, допущения, принципы, принимаемые в курсе сопротивления материалов
Методы расчета на прочность и жесткость конструкции в сопротивлении материалов основаны на применении следующих гипотез и допущений.
1. Материал конструкции считается сплошным и однородным. Атомистическая теория строения вещества в расчет не принимается.
Исключение: допущение неприемлемо при рассмотрении усталостной природы разрушения металлов.
2. Материал конструкции считается анизотропным, то есть обладает одинаковыми свойствами во всех направлениях.
Исключение: дерево, прокатный материал.
3. Материал конструкции подчиняется закону Гука
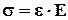 - для линейных деформаций;
- для линейных деформаций;
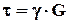 - при деформациях сдвига.
- при деформациях сдвига.
4. Материал тела считается абсолютно упругим.
5. Поперечные и нормальные к оси сечения бруса до приложения нагрузки остаются плоскими и нормальными после приложения нагрузки (Гипотеза Бернулли или гипотеза плоских сечений).
6.
|
|


|


 Принцип суперпозиции. Результат действия на конструкцию суммы нагрузок равен сумме результатов действия каждой нагрузки отдельно (рис. 5.1).
Принцип суперпозиции. Результат действия на конструкцию суммы нагрузок равен сумме результатов действия каждой нагрузки отдельно (рис. 5.1).
| |||||||||
 | |||||||||
 | |||||||||
 | |||||||||
 |
Рис. 5.1 Принцип суперпозиции
7.
|


|
|

 Принцип Сен-Венана. На расстоянии равном размеру поперечного сечения бруса способ приложения нагрузки не оказывает влияния на напряженно деформированное состояние бруса (рис. 5.2).
Принцип Сен-Венана. На расстоянии равном размеру поперечного сечения бруса способ приложения нагрузки не оказывает влияния на напряженно деформированное состояние бруса (рис. 5.2).  |
Рис. 5.2 Принцип Сен-Венана
8. Деформации конструкции малы и не влияют на взаимное положение точек приложения внешних сил и изменение размеров конструкции.
6. Расчеты на прочность и жесткость при растяжении и сжатии
Растяжение – такой вид нагружения, при котором в поперечном сечении стержня возникают только нормальные силы N, а все остальные внутренние силовые факторы (поперечные силы, крутящий и изгибающий моменты) равны нулю.
Приложение нормальных сил к стержню может быть различным, но в любом случае система внешних сил образует равнодействующую Р, направленную вдоль оси стержня, то есть во всех поперечных сечениях стержня возникают нормальные силы N, равные силе Р: N=P.
При расчетах в сопротивлении материалов сжатие отличается от растяжения формально только знаком силы N.
Таким образом, при рассмотрении задач сохраняется единство подхода к вопросам растяжения и сжатия.
Если для нагруженного по концам растянутого однородного стержня напряжения остаются постоянными как по сечению, так и по длине, то такое напряженное состояние называется однородным.
Рассмотрим задачу о распределении напряжений 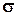 и
и 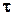 при растяжении (сжатии) в поперечном сечении стержня (рис. 6.1).
при растяжении (сжатии) в поперечном сечении стержня (рис. 6.1).
Три стороны задачи о растяжении и сжатии стержня.
 2015-02-27
2015-02-27 2329
2329
