Сравнение алгоритмов на основе функции трудоемкости

Итак, под трудоемкостью алгоритма для данной конкретной проблемы, заданной множеством D, понимают количество элементарных операций, задаваемых алгоритмом в принятой модели вычислений. В качестве модели вычислений рассматривают абстрактную машину, имеющую процессор с фон- Неймановской архитектурой, адресную память и набор элементарных операций, соответствующий языкам высокого уровня. Такая модель вычислений называется машиной с произвольным доступом к памяти (RAM).

Функция трудоемкости f_A (D) – это отношение, которое связывает входные данные с количеством элементарных операций. Значением этой функции является целое положительное число.

Опыт показывает, что количество элементарных операций, задаваемых алгоритмом, то есть значение f_A (D) на входе длины n, где n=|D|, не всегда совпадает с количеством операций на другом входе такой же длины. (потому что существует много множеств D длины n – то есть может быть много различных входных наборов данных)

Поэтому при анализе алгоритмов различают худший случай, лучший случай, и средний случай.

Худший случай – это наибольшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.

Лучший случай – это наименьшее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.

Средний случай – среднее количество операций, совершаемых алгоритмом А для решения конкретных проблем размерности n.

Для получения значений функции трудоемкости f_A (D) определили элементарные операции, используемые в языках высокого уровня, которые необходимо учитывать при расчетах.

Такими операциями являются:

Операция присваивание: а = b;

Одномерная индексация a[i]: (адрес (a)+i*длина элемента);

Арифметические операции: (*, /, -, +);

Операции сравнения: a < b;

Логические операции {or, and, not};

Конструкция «Следование» Трудоемкость конструкции есть сумма трудоемкостей блоков, следующих друг за другом, где k – количество блоков.

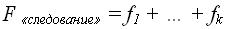
Конструкция «Ветвление»

if(условие) then (блок с трудоемкостью f_then и вероятностью p)

else (блок с трудоемкостью f_else и вероятностью (1-p)

Общая трудоемкость конструкции «Ветвление» требует анализа вероятности выполнения переходов на блоки «then» и «else» и определяется как:

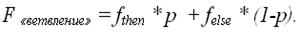
К этому придется еще добавить трудоемкость вычисления условия.

Для анализа худшего случая выбирается тот блок ветвления, который имеет большую трудоемкость, а для лучшего – тот, трудоемкость которого минимальна.

Конструкция “Цикл”

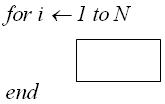
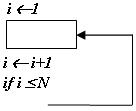
Общая трудоемкость определяется как

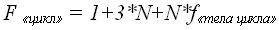
Примеры анализа трудоемкости алгоритмов.

Пример 1 Задача суммирования элементов квадратной матрицы

SumM (A, n; Sum)

Sum =0 // 1 операция

For i = 1 to n // 3 операции на один проход цикла

For j = 1 to n // 3 операции на один проход цикла

Sum =Sum + A[i,j] // 4 операции

End for j

End for i

Return (Sum)

End.

Алгоритм выполняет одинаковое количество операций при фиксированном значении n, и, следовательно, является количественно-зависимым. Его функция трудоемкости зависит только от размерности конкретного входа. Применение методики анализа конструкции «Цикл» дает:

f_A(n)=1+1+ n *(3+1+ n *(3+4))=7*n²+4* n +2 = (n²),

где внутренний цикл: f₁(n) = 1+3*n+4*n

внешний цикл: f₂(n)= 1+3*n+n*f₁(n)

замечание по задаче:

под n понимается линейная размерность матрицы, в то время как на вход алгоритма подается n² значений.

Общее замечание:

Количественно-зависимые по трудоемкости алгоритмы - это алгоритмы, функция трудоемкости которых зависит только от размерности конкретного входа, и не зависит от конкретных значений:

Fa(n), n=f(N)

К ним можно отнести алгоритмы для стандартных операций с массивами и матрицами – умножение матриц, умножение матрицы на вектор и т.д.

Пример 2 Задача поиска максимума в массиве

MaxS (S,n; Max)

Max = S[1] // 2 операции

For i = 2 to n // 3 операции на один проход цикла

if Max < S[i] // 2 операции

then Max =S[i] // 2 операции

end for

return Max

End

Данный алгоритм является количественно-параметрическим.

Трудоемкость таких алгоритмов определяется количеством данных на входе и значениями этих данных:

Fa(n), n=f(N,р1…,рi)

В данном конкретном случае трудоемкость зависит от размера входа и от порядка расположения однородных элементов. Зависимость от значений не может быть полностью исключена, но она не является существенной, поэтому для фиксированной размерности исходных данных необходимо проводить анализ для худшего, лучшего и среднего случая. Примерами такого класса могут служить алгоритмы сортировки сравнениями, алгоритмы поиска минимума и максимума в массиве.

А). Худший случай

Максимальное количество переприсваиваний максимума (на каждом проходе цикла) будет в том случае, если элементы массива отсортированы по возрастанию. Трудоемкость алгоритма в этом случае равна:

f_A(n)=1+1+1+ (n-1) (3+2+2)=7 n - 4 = (n).

Б) Лучший случай

Минимальное количество переприсваивания максимума (ни одного на каждом проходе цикла) будет в том случае, если максимальный элемент расположен на первом месте в массиве. Трудоемкость алгоритма в этом случае равна:

f_A(n)=1+1+1+ (n-1) (3+2)=5 n - 2 = (n).

В) Средний случай

Алгоритм поиска максимума последовательно перебирает элементы массива, сравнивая текущий элемент массива с текущим значением максимума. На очередном шаге, когда просматривается к-ый элемент массива, переприсваивание максимума произойдет, если в подмассиве из первых “к” элементов максимальным элементом является последний. Очевидно, что в случае равномерного распределения исходных данных, вероятность того, что максимальный из к элементов расположен в определенной (последней) позиции равна 1/к. Тогда в массиве из n элементов общее количество операций переприсваивания максимума определяется как:

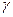-постоянная Эйлера

Величина Hn называется n-ым гармоническим числом. Таким образом, точное значение (математическое ожидание) среднего количества операций присваивания в алгоритме поиска максимума в массиве из n элементов определяется величиной Hn (при очень большом количестве испытаний)), тогда:

f_A(n)=1 + (n-1) (3+2) + 2 (ln (n) + 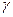)=5 n +2 ln(n) - 4 +2 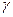= (n).

(В сущности это есть математическое ожидание среднего количества операций присваивания в алгоритме поиска максимума в массиве их n элементов. При этом мы предполагаем, что значения элементов распределены равномерно)

[Анализ сложности рекурсивных алгоритмов будет разобран на практике №3-4 для задачи вычисления факториала для некоторого значения n (n – параметр алгоритма, а не количество слов на входе)]