Описание движения частицы в квантовой механике. Волновая функция

Центральным понятием квантовой механики является волновая функция 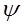, которая по аналогии с гармоническими колебаниями и волнами характеризует амплитуду (распределение) стоячих волн в пространстве. Данное понятие было введено в квантовую механику Э. Шрёдингером. Волновая функция зависит от координат 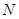частиц, т.е. от радиус-векторов 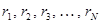и в общем случае от времени 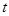и обозначается 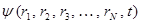, тогда общее решение дифференциального уравнения для гармонического осциллятора в показательной форме вида:

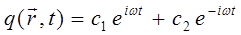
может быть записано в виде:

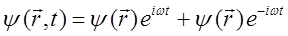
где выражения:

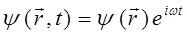
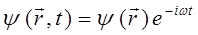
частные решения соответствующего дифференциального уравнения. Необходимо отметить, что одно из частных решений будет комплексно сопряжённым другому. При этом суперпозиция соответствующих частных решений, образуют стоячую волну, состоящую из двух бегущих волн. Поскольку волновая функция 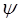- комплексная величина, т.е.

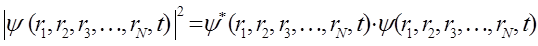
то физический смысл будет иметь не сама волновая функция 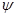, а квадрат её модуля 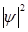. По аналогии со световыми волнами, квадрат амплитуды 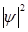пропорционален интенсивности волны. Интенсивность волны, с точки зрения квантовой теории света, равнозначна числу световых квантов (фотонов) в единице объёма, а для единичного фотона – вероятности его нахождения в единице объёма. Проводя аналогию между светом и веществом далее, можно считать, что интенсивность волны де Бройля или 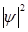определяет число частиц в единице объёма. Если рассматривать единичную частицу, то квадрат амплитуды 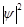даёт вероятность нахождения частицы в единице объёма или плотность вероятности:

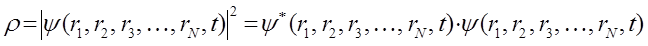
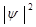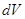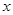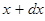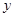Очевидно, произведение плотности вероятности на элементарный объём - есть вероятность нахождения частицы в элементарном объёме, т.е. в области с координатами и 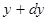, 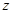и , и 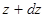. Таким образом, амплитуда волны де Бройля получает статистическое истолкование, а для единичной частицы – вероятностное толкование. Квадрат амплитуды волны де Бройля 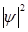равен вероятности нахождения частицы в единице объёма, её плотности вероятности. Аналитически данное положение, являющееся одним из постулатов квантовой механики, задаётся выражением вида:

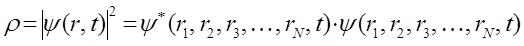
откуда соответственно:

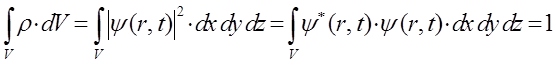
Этот постулат был выдвинут впервые в 1928 г. М. Борном. Таким образом, волны де Бройля – это волны вероятности, они не материальны, т.е. не связаны с каким-либо переносом энергии. Отсюда становится понятным, почему при рассмотрении волнового процесса, в качестве модели выбирают так называемые стоячие волны, распространение которых не связано с переносом энергии и потому являющиеся стабильными, постоянными во времени. Итак, в квантовой механике описание состояния частицы (или системы частиц) выполняется с помощью волновой функции 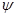, которая описывает распределение вероятностей нахождения этой частицы (или системы частиц) в пространстве. Статистическая интерпретация 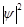как вероятности нахождения частицы в элементе объёма 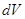, находится в полном соответствии с принципом неопределённости Гейзенберга. В оптике волновая функция находится как решение дифференциального уравнения волны. Аналогично в квантовой механике существует дифференциальное уравнение для волн де Бройля, из которого находят волновую функцию описывающую распределение электронной плотности в микросистемах. Для вывода такого уравнения на основании оптико-механической аналогии Гамильтона, найдём изначально стационарные решения волнового уравнения, строго зависящие от частоты 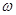, имеем соответственно:

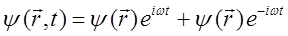
При этом получаемые решения должны удовлетворять требованиям регулярности и граничному условию. К требованиям регулярности относят: конечность, однозначность, и непрерывность волновой функции. Требование конечности означает, что величины 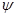и 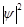не могут принимать бесконечно большие значения. Однозначность волновой функции означает, что вероятность найти частицу в данном элементарном объёме 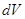- всегда строго определённая, большая или малая, но всегда одна. Непрерывность волновой функции 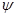означает, что нет такого элементарного объёма 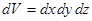, где нельзя было бы определить вероятность нахождения микрочастицы. Граничное условие – обращение волновой функции 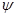в нуль на бесконечности. Данное условие означает, что частицу всегда можно найти в каком-то строго локализованном участке пространства. Кроме того, волновая функция должна подчиняться условиям нормировки и ортогональности. Ортогональные и нормированные волновые функции называют также ещё ортонормированными. Условие одновременной ортогональности и нормированности волновой функции 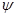можно записать также с использованием символа Кронекера. Тогда исходя из физического смысла таких понятий как нормировка и ортогональность векторов состояния в так назщываемом непрерывном представлении, можно записать, что:

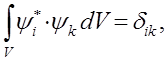
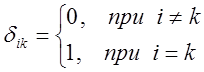
Основываясь на хорошо известной из математики теореме о полной вероятности, можно утверждать, что вероятность обнаружить частицу во всём объёме равна сумме вероятностей во всех точках этого пространства и равна единице:

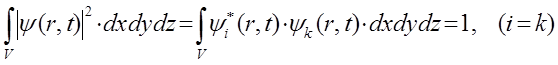
Таким образом, условие нормировки является следствием этой математической теоремы. Действительно, если электрон находится в некотором объёме и известна волновая функция электрона 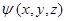. Тогда при разбиении объёма 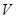на бесконечно малое число элементарных объёмов 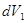, , 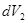, 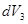…, , 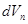вероятность обнаружить электрон в каждом из элементарных объёмов будет очевидно определяться выражениями вида:

.……………………….

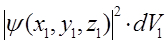
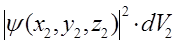
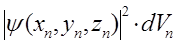
Поскольку вероятность достоверного события равна единице, то очевидно полная вероятность (вероятность нахождения электрона во всём объёме 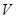) равна сумме вероятностей отдельных событий и равна единице:

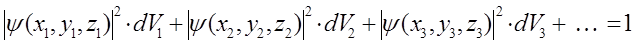
Переходя к бесконечно малым элементам объёма, суммирование можно заменить интегралом вида:

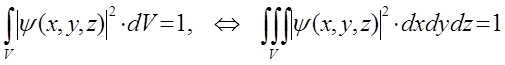
Из условия нормировки также следует, что волны вероятност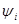и и 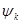соответствуют одинаковым состояниям микрочастицы. Нормированность волновой функции показывает, что вероятность нахождения микрочастицы в элементарном объёме 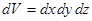всегда конечна и равна единице. Ортогональность волновых функций определяется выражением вида:

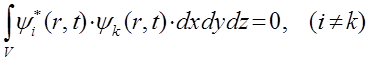
откуда следует, что волны вероятност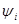и и 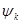соответствуют различным состояниям микрочастицы. Ортогональность волновых функций определяет их линейную независимость, т.е. не одна из них не содержит в себе примеси другой, в чём хорошо проявляется принцип суперпозиции состояний системы. Таким образом, состояние частицы (системы частиц) в любой момент времени полностью описывается волновой функцией, характеризующей распределение стоячих волн в пространстве. Поскольку по определению волновая функция 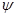должна быть конечной, т.е. величины 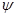и 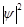не могут принимать бесконечно большие значения, тогда в соответствии с принципом конечности, стационарное (не зависящее от времени), решение выбираем в виде:

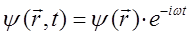
Рассматривая для простоты выкладок одномерный случай, будем иметь соответственно:

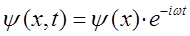
Легко показать, что выбранное в соответствии с описанными выше физически осмысленными условиями решение, соответствует уравнению плоской волны де Бройля, имеющей вид:

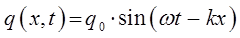
Итак, имеем соответственно:

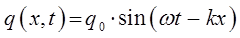
или в экспоненциальном виде:

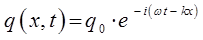
откуда следует соответственно, что:

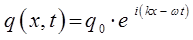
Учитывая, что величине смещения 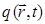, амплитуды волны в квантовой механике соответствует волновая функция 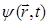, тогда соответственно:

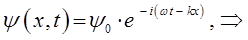
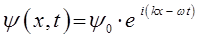
Из полученного уравнения достаточно хорошо видно, что волновая функция 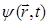есть произведение координатной волновой функции на член, выражающий зависимость её от времени, т.е.

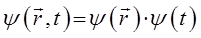
тогда соответственно выражение:

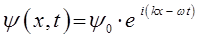
может быть представлено к виду:

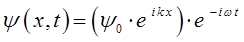
и далее соответственно:

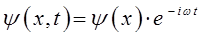
Итак, как было показано выше, выражение для волновой функции 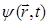может быть представлено выражением вида:

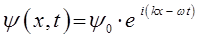
Учитывая, что:

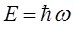
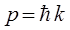
откуда:

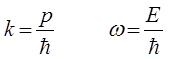
имеем соответственно:

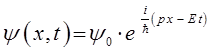
выражение волновой функции де Бройля для свободной частицы, движущейся вдоль оси Ox. Аналогично, для частицы, движущейся вдоль некоторого направления 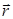с постоянным радиальным импульсом 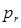, волновая функция де Бройля, очевидно, будет иметь вид:

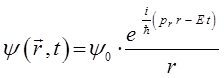
Если же учесть, что 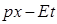совпадает с действием 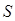для свободной частицы:

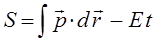
и вспомнить более общее соотношение вида:

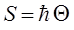
предлагаемое оптико-механической аналогией, то можно было бы ожидать, что для произвольного (несвободного) движения волновая функция 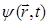получается из выражения:

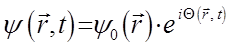
тогда с учётом уравнения:

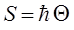
откуда:

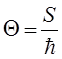
имеем соответственно:

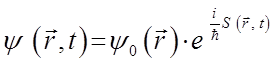
Однако волновая функция, взятая в таком виде, не могла привести к пониманию свойств электронов в атомах и более сложных структурах – молекулах, кристаллах, кластерах, плёнках. Это связано с тем, что в полученном выражении по-прежнему сохранялись классические концепции – действие и механическая траектория частицы. Анализ процедуры измерения для микрочастиц показал невозможность сохранения понятия траектории в микромире. Следующее наглядное рассуждение, принадлежащее Гейзенбергу и Бору, поясняет общий принцип, известный как принцип неопределённости Гейзенберга.