Последовательность независимых испытаний (схема Бернулли)

Рассмотрим некоторое испытание и связанное с ним случайное событие А. Пусть это испытание повторяется многократно при неизменных условиях. В таком случае говорят, что производится последовательность независимых испытаний (иногда это называется схемой Бернулли).

Примером является игра двух сторон на определенных условиях (бросание монеты или кубика, шахматы, карточные игры, лотереи, тотализаторы и т.п.), событие А – это выигрыш одной из сторон в данной игре. В схеме Бернулли принято событие А называть “успехом”, а противоположное ему событие `А – “неудачей”.

Предположим, что производится серия из n независимых испытаний с двумя исходами (“успех” или “неудача”) в каждом испытании; р – вероятность “успеха”; q=1-р – вероятность “неудачи” (обычно р и q либо заданы, либо легко вычисляются). Обозначим через k число успехов в этой серии, которое может принимать любые значения от 0 до n. Событие M_k, состоящее в том, что число успехов в нашей серии испытаний окажется равным именно числу k, является случайным. Его вероятность Р (M_k) (обозначают через Р_n(k)) может быть найдена по формуле Бернулли (Якоб Бернулли (1654 – 1705) – швейцарский математик):

P_n(k)=C^k_np^kq^n–k

(доказательство формулы Бернулли можно получить, используя формулы сложения и умножения вероятностей).

Рассмотрим некоторые примеры.

Задача 1. Монету бросают 10 раз. Найти вероятность того, что число выпавших “орлов” и “решек” будут одинаковым.

Решение. Пусть успех – это, например, выпадение орла при одном бросании, тогда р=q=1/2. Общее число испытаний n=10, число успехов k равно 5. Значит, по формуле Бернулли:

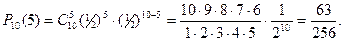
Задача 2. Кубик бросают 4 раза. Какова вероятность того, что не меньше двух раз выпадет цифра, большая четырех?

Решение. Будем понимать под успехом выпадение на кубике при одном бросании цифры, большей четырех (т.е. 5 или 6). Очевидно, вероятность успеха р=2/6=1/3; (q=2/3). Общее число испытаний n=4. Число успехов k должно быть равно 2, 3 или 4. Поэтому, применяя три раза формулу Бернулли, получим искомую вероятность

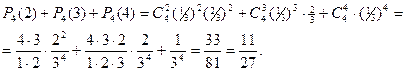
Задача 3. Вероятность попадания в цель при одном выстреле равна р=1/2. Известно, что для полного поражения цели требуется не менее трех попаданий. Какое минимальное количество выстрелов нужно произвести, чтобы с вероятностью не менее, чем 0.9, можно было утверждать, что цель поражена.

Решение. Предположим, что по цели произведено n выстрелов. Тогда вероятность поражения цели будет равна:

р_n(3)+р_n(4)+... +р_n(n)=1-p_n(0)-p_n(1)-p_n(2).

Минимальное число выстрелов, очевидно, определяется неравенством:

р_n(3)+р_n(4)+... +р_n(n)³0,9 или

р_n(0)+р_n(1)+р_n(2)£0,1.

Отсюда по формуле Бернулли:

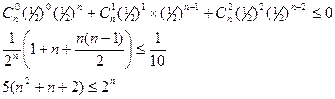
Легко убедиться в том, что это неравенство будет выполняться, начиная с n=9. Таким образом, минимальное число выстрелов для поражения цели с вероятностью 0.9 будет равно 9.

Из рассмотренных примеров видно, что формулой Бернулли нетрудно пользоваться, если число испытаний n невелико. На практике же встречаются серии из нескольких десятков, сотен и даже тысяч испытаний. В таких случаях формула Бернулли практически непригодна и вместо нее используют приближенные формулы, о которых пойдет речь несколько позже.