Решение системы нелинейных уравнений с двумя неизвестными с помощью средства Поиск решения

Надстройка Поиск решения позволяет находить решение системы нелинейных уравнений с двумя неизвестными:

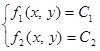, (18)

где f_i (x,y), i = 1,2 – нелинейная функция от переменных х и у;

С_i, i = 1,2 – произвольная постоянная.

Известно, что пара (х, у) является решением системы уравнении (18) тогда и только тогда, когда она является решением следующегонелинейного уравнения с двумя неизвестными:

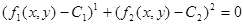. (19)

С другой стороны, решение системы (18) – это точки пересечения двух кривых: f₁(x, y) = C₁ и f₂(х, у) = С₂ на плоскости XOY.

Из этого следует метод нахождения корней системы нелинейных уравнений.

1. Определить (хотя бы приближенно) интервал существования решения системы уравнений (18) или уравнения (19). Здесь необходимо учитывать вид уравнений, входящих в систему, область определения каждого их уравнений и т.п. Иногда применяется подбор начального приближения решения.

2. Протабулировать решение уравнения (19) по переменным х и у на выбранном интервале, либо построить графики функций f₁(х, у) = С₁ и f₂(x, y) = C₂ (система (18).

3. Локализовать предполагаемые корни системы уравнений – найти несколько минимальных значений из таблицы табулирования корней уравнения (19), либо определить точки пересечения кривых, входящих в систему (18).

4. Найти корни для системы уравнений (18) с помощью надстройки Поиск решения.

Пример 4. Решить следующую систему нелинейных уравнений:

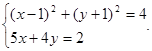
Решение. Решением системы уравнений являются точки пересечения окружности (с радиусом 2 и центром (1, -1) и прямой

у = 0,5-1,25 x.

Данную систему заменим равносильным уравнением:

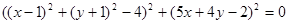для которого будем искать решения с помощью надстройки Поиск решения.

1. Исходя из графиков уравнений интервал локализации корней определим в границах от -3 до 3 (рис. 28). Ячейки В3:В43 содержат значения Х.

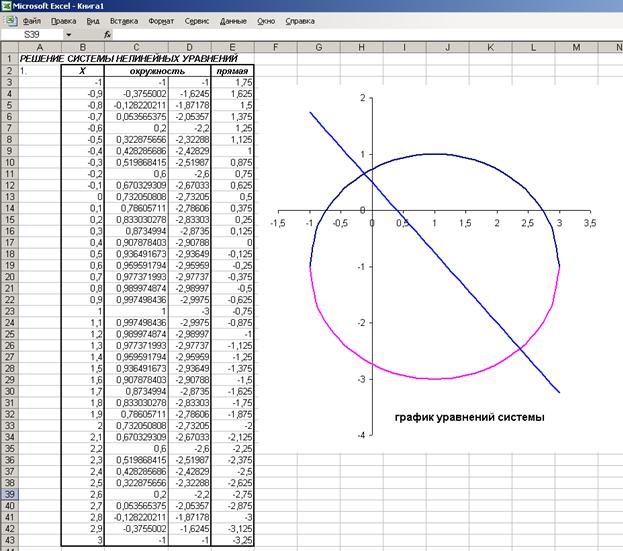
Рис. 28. Графическое решение системы нелинейных уравнений

Формулы для построения графиков:

- в ячейки С3:

= -1+КОРЕНЬ(4-(B3-1)^2;

- в ячейки D3:

= -1-КОРЕНЬ(4-(B3-1)^2);

- в ячейки E3:

= (2-5*B3)/4.

2. Табулируем равносильное уравнение на отрезке [-3; 3] c шагом 0,5 (рис. 29).

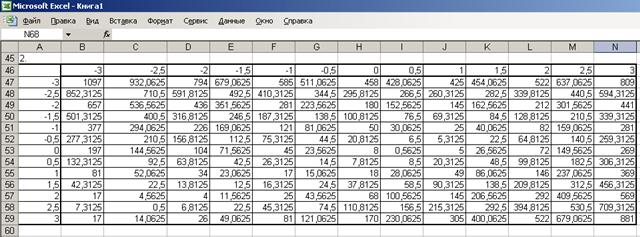
Рис. 29. Табулирование функции для нахождения решения

системы уравнений

3. Локализуем корни равносильного уравнения (рис. 30):

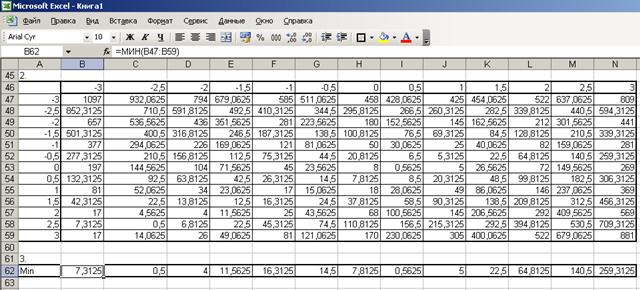
Рис. 30. Локализация корней системы уравнений

- ячейки A47:A59 cодержат значения Х на отрезке [-3; 3] с шагом 0,5;

- ячейки В46:N46 содержат значения Y на отрезке [-3; 3] с шагом 0,5;

- формула для ячейки В47 (копируем на диапазон B47:N59):

=(($A47-1)^2+(B$46+1)^2-4)^2+(5*$A47+4*B$46-2)^2;

- формула для ячейки В62 (копируем на диапазон B62:N62):

= МИН(B47:B59)

Исходя из результатов вычислений следующие пары предполагаемых корней уравнения: (-2,5; -2,5), (2; -2), (0; 0,5) и (0;1).

4. Найдем корни равносильного уравнения (рис. 31) – для этого поместим пары значений для предполагаемых корней в ячейки D69:E72. В ячейку G69 введем формулу для равносильного уравнения (копируется на диапазон G69:G72):

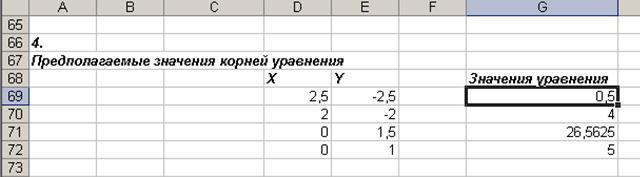
Рис. 31. Подготовка листа рабочей книги для нахождения корней нелинейной системы уравнений

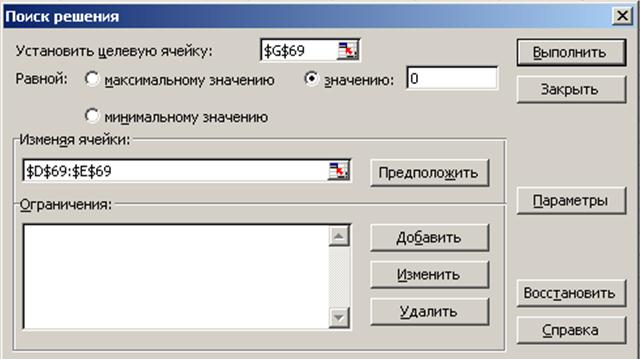
Рис. 32. Ввод данных в окно Поиск решения для задачи нахождения корней системы уравнений

С помощью надстройки Поиск решения (в окне Параметры поиска решения (рис. 32) флажок Линейная модель должен быть снят) установим необходимые параметры для поиска корня равносильного уравнения (рис. 33), затем выполним поиск решения. Процедуру повторим для всех имеющихся пар корней.

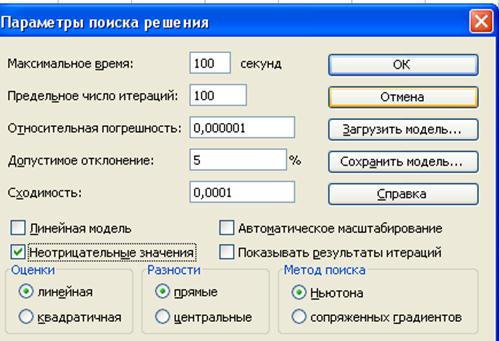
Рис. 33. Окно Параметры поиска решения

Результаты поиска решения (рис. 34) позволяют сделать вывод о том, что система имеет 2 решения: (2,3675745729901; -2,45934248863711) и (-0,123564081639673; 0,654434224216163).

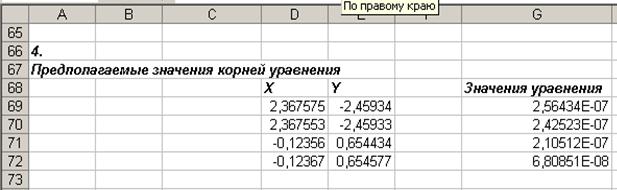
Рис. 34. Результаты поиска решения для нелинейной системы уравнений

5. Балансовые модели

5.1. Экономико-математическая модель межотраслевого баланса (модель Леонтьева)

Рассмотрим наиболее простой вариант модели межотраслевого баланса (ее называют моделью Леонтьева, или моделью «затраты – выпуск»).

Алгебраическая теория анализа модели «затраты – выпуск» сводится к решению системы линейных уравнений, в которых параметрами являются коэффициенты затрат на производство продукции.

Пусть весь производственный сектор народного хозяйства разбит на п «чистых» отраслей. «Чистая» отрасль – это условное понятие, некоторая часть народного хозяйства, более или менее цельная (например, энергетика, машиностроение, сельское хозяйствои т.п.).

Пусть X_ij – объем продукции отрасли i, расходуемый в отрасли j; Х_i – объем производства отрасли i за данный промежуток времени (так называемый валовой выпуск продукции i); Y_i – объем потребления продукции отрасли i в непроизводственной сфере (объем конечного потребления); Ζ_ј – условно чистая продукция, которая включает в себя оплату труда, чистый доход и амортизацию.

Единицы измерения всех указанных величин могут быть или натуральными (кубометры, тонны, штуки и т.п.), или стоимостными. В зависимости от этого различают натуральный и стоимостной межотраслевые балансы. Ниже мы будем рассматривать стоимостной баланс. В таблице 8 представлена принципиальная схема межотраслевого баланса в стоимостном выражении.

Таблица 8

Матрица межотраслевого баланса (в общем виде)

Производящие отрасли	Потребляющие отрасли	Конечный продукт	Валовой продукт
1	2	…	n
1	Х₁₁	Х₁₂	…	Х_1n	Y₁	Х₁
2	Х₂₁	Х₂₂	…	Х_2n	Y₂	Х₂
…	…	…	…	…	…	…
n	Х_n1	Х_n2	…	Х_nm	Y₃	Х_n
Условно чистая продукция	Z₁	Z₂	…	Z_n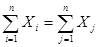
Валовой продукт	Х₁	Х₂	…	X_n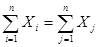

Рассматривая схему баланса по столбцам, можно заметить, что итог материальных затрат любой потребляющей отрасли и ее условно чистой продукции равен валовой продукции этой отрасли. Данный вывод можно записать в виде соотношения:

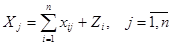. (20)

Напомним, что величина условно чистой продукции Ζ_ј равна сумме амортизации, оплаты труда и чистого дохода отрасли j. Данноесоотношение охватывает систему из п уравнений, отражающих стоимостный состав продукции всех отраслей материальной сферы.

Рассматривая схему МОБ по строкам для каждой производящей отрасли, замечаем, что валовая продукция той или иной отрасли равна сумме материальных затрат потребляющих ее продукцию отраслей и конечной продукции данной отрасли:

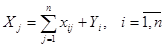. (21)

Формула (21) описывает систему из n уравнений, которые называются уравнениями распределения продукции отраслей материального производства по направлениям использования.

Балансовый характер таблицы выражается в том, что

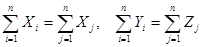Коэффициенты прямых материальных затрат. Основу экономико-математической модели МОБ составляет технологическая матрица коэффициентов прямых затрат А (а_ij).

Коэффициент прямых материальных затрат а_ij показывает, сколько необходимо единиц продукции отрасли i для производства единицы продукции отрасли j, если учитывать только прямые затраты:

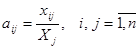. (22)

Сделаем два важных предположения, необходимых для дальнейшего рассмотрения модели Леонтьева.

1. Сложившуюся технологию производства считаем неизменной. Таким образом, матрица А = (а_ij) постоянна.

2. Постулируем свойство линейности существующих технологий: для выпуска отраслью j любого объема продукции X_j необходимо затратить продукцию отрасли i в количестве a_ijX_j, т.е. материальные издержки пропорциональны объему производимой продукции:

x_ij = a_ijX_j. (23)

Подставляя (23) в балансовое соотношение (21), получаем

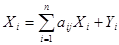, (24)

или в матричной форме

X=AX+Y. (25)

С помощью этой модели можно выполнять три вида плановых расчетов:

– задавая для каждой отрасли величины валовой продукции (X_i), можно определить объемы конечной продукции каждой отрасли (Y_i):

Y= (Е - А)Х; (26)

– задавая величины конечной продукции всех отраслей (Y_i), можно определить величины валовой продукции каждой отрасли (X_i):

Х = (Е - А)^-1Y; (27)

– задавая для ряда отраслей величины валовой продукции, а для всех остальных отраслей – объемы конечной продукции, можно найти величины конечной продукции первых отраслей и объемы валовой продукции вторых.

В формулах (26) и (27) символ Е обозначает единичную матрицу порядка n, а (Е - А)^-I – матрицу, обратную к матрице (Е - А).

Если определитель матрицы (Е - А) не равен нулю, т.е. эта матрица невырожденная, то существует обратная к ней матрица. Обозначим обратную матрицу через В = (Е - А)^- ¹, тогда систему уравнений в матричной форме (8) можно записать в виде Х = ВY.

Элементы матрицы В называются коэффициентами полных материальных затрат. Они показывают, сколько всего нужно произвести продукции отрасли i для выпуска в сферу конечного использования единицы продукции отрасли j. Плановые расчеты по модели Леонтьева можно выполнять, если соблюдается условие продуктивности.

Неотрицательную матрицу А будем называть продуктивной, если существует такой неотрицательный вектор Х ≥ 0, что

Х > АХ. (28)

Очевидно, что условие (9) означает существование положительного вектора конечной продукции Y > 0 для модели межотраслевого баланса (25).

Для того чтобы матрица коэффициентов прямых материальных затрат А была продуктивной, необходимо и достаточно, чтобы выполнялось одно из перечисленных ниже условий:

1) матрица (Е - А) неотрицательно обратима, т.е. существует обратная матрица (Е - А)^-1≥ 0;

2) матричный ряд Е + А + А² + А^З +... = 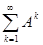сходится, причемего сумма равна обратной матрице (Е - A)^-1:

В = (Е – А) ^-I = Е + А + А² + А^З +...; (29)

3) наибольшее по модулю собственное значение λматрицы А, т.е. решение характеристического уравнения │λ Е–А │= 0 строго меньше единицы;

4) все главные миноры матрицы (Е – А), т.е. определители матриц, образованные элементами первых строк и первых столбцов этой матрицы, порядка от 1 до n положительны.

Более простым способом проверки продуктивности матрицы А является ограничение на величину её нормы, в данном случае на величину наибольшей из сумм элементов матрицы в каждом столбце. Если норма матрицы А строго меньше единицы, то эта матрица продуктивна. Данное условие является достаточным, но не необходимым условием продуктивности, поэтому матрица А может оказаться продуктивной и в случае, когда её норма больше единицы.

Пример 5. Даны коэффициенты прямых затрат а_ij и конечный продукт Y_j для трехотраслевой экономической системы:

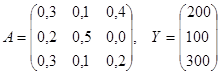
Требуется определить:

1) коэффициенты полных затрат;

2) вектор валового выпуска;

3) межотраслевые поставки продукции;

4) проверить продуктивность матрицы А;

5) заполнить схему межотраслевого баланса.

Для решения задачи воспользуемся функциями Excel.

В таблице 9 приведены результаты решения задачи по первым трем пунктам.

1. Вычислим матрицу коэффициентов полных затрат В = (Е – А)^-1.

Таблица 9

Решение модели межотраслевого баланса

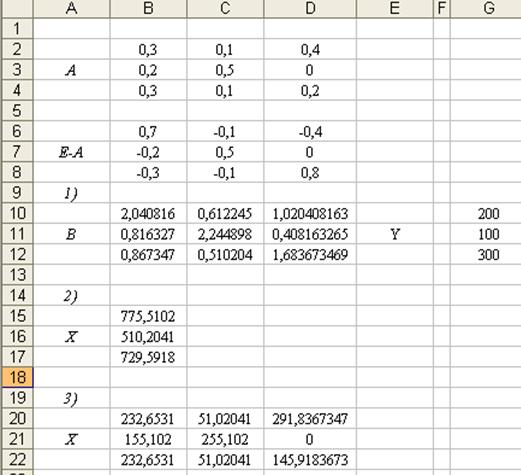
Для вычисления обратной матрицы необходимо:

•выделить диапазон ячеек для размещения обратной матрицы;

•выбрать функцию МОБР в категории Математические;

•ввести диапазон ячеек, где содержится матрица Е – А;

•нажать клавиши CTRL+SHIFT+ENTER.

В ячейки B6:D8 запишем элементы матрицы Е – А. Массив Е – А задан как диапазон ячеек. Выделим диапазон B10:D12 для размещения обратной матрицы В = (E — A)^-1 и введем формулу для вычислений МОБР (B6:D8). Затем следует нажать клавиши CTRL+SHIFT+ENTER.

Все элементы матрицы коэффициентов полных затрат В неотрицательны, следовательно, матрица А продуктивна (это ответ на пункты 1 - 3).

2. Вычислим вектор валового выпуска X по формуле X = BY.

Для умножения матриц необходимо:

выделить диапазон ячеек для размещения результата умножения матриц;

выбрать функцию МУМНОЖ в категории Математические;

ввести диапазоны ячеек, где содержатся матрицы В и Y;

нажать клавиши CTRL+SHIFT+ENTER.

В ячейки G10:G12 запишем элементы вектора конечного продукта Y. Выделим диапазон В15:В17 для размещения вектора валового выпуска X, вычисляемого по формуле Х= (Е – А)^-1 Y. Затем вводим формулу для вычислений МУМНОЖ (B10:D12, G10:G12). Далее следует нажать клавиши CTRL+SHIFT+ENTER.

3. Межотраслевые поставки x_ij вычисляем по формуле x_ij = a_ijX_j.

4.Заполняем схему МОБ (табл. 10).

Таблица 10

Схема межотраслевого баланса

Производящие отрасли Потребляющие отрасли Конечный продукт Валовой продукт

1 2 3

1 232,6 51,0 291,8 775,3

2 155,1 255,0 0,0 510,1

3 232,6 51,1 145,9 729,6

Условно чистая продукция 155,0 153,1 291,9

Валовой продукт 775,3 510,1 729,6

Найдем условно чистую продукцию Z:

1) рассчитать полученную сумму в потребляющих отраслях;

2) найти разницу между объемом валового продукта потребляющей отрасли и объем потребления в каждой отрасли.

Найдем баланс в общем распределении продукции между производящими и потребляющими отраслями:

1) в балансе конечный продукт должен быть равен условно чистой продукции;

2) валовой продукт в потребляющих отраслях должен быть равен валовой продукции в производящих отраслях.

5.2. Межотраслевые балансовые модели в анализе экономических показателей

К числу важнейших аналитических возможностей данного балансового метода относится определение прямых и полных затрат труда на единицу продукции и разработка на этой основе балансовых продуктово-трудовых моделей. При этом исходной моделью служит отчетный межпродуктовый баланс в натуральном выражении. В отдельной строке баланса дается распределение затрат живого труда в производстве всех видов продукции. Предполагается, что трудовые затраты выражены в единицах труда одинаковой степени сложности.

Пусть Lj – затраты живого труда в производстве продукта j, а Х_j – объем производства этого продукта (валовой выпуск). Тогда прямые затраты труда на единицу продукции вида j (коэффициент прямой трудоемкости) можно задать следующей формулой:

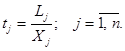(1)

Введем понятие полных затрат труда как суммы прямых затрат живого труда и затрат овеществленного труда, перенесенных на продукт через израсходованные средства производства. Если обозначить величину полных затрат труда на единицу продукции вида j через T_j, то произведения вида a_ijT_i отражают затраты овеществленного труда, перенесенного на единицу продукта j через средство производства i. Предположим, что коэффициенты прямых материальных затрат a_ij выражены в натуральных единицах. Тогда полные трудовые затраты на единицу продукции вида j (коэффициент полной трудоемкости) будут равны

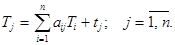(2)

Введем вектор-строку коэффициентов прямой трудоемкости 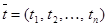и вектор-строку коэффициентов полной трудоемкости 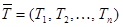. Тогда с помощью матрицы коэффициентов прямых материальных затрат А (в натуральном выражении) систему (2) можно переписать в матричном виде

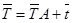. (3)

Произведя очевидные матричные преобразования с использованием единичной матрицы Е

,

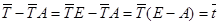получим следующее соотношение для вектора коэффициентов полной трудоемкости:

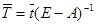. (4)

Матрица (Е - А) ^-1 нам уже знакома, это матрица коэффициентов полных материальных затрат – В, поэтому равенство (4) можно переписать в виде:

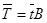. (5)

Обозначим через L величину совокупных затрат живого труда по всем видам продукции, которая с учетом формулы (1) будет равна

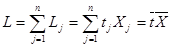. (6)

Используя соотношения (X>AX), (5) и (6), приходим к следующему равенству:

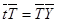. (7)

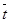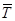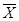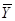Здесь и – векторы-строки коэффициентов прямой и полной трудоемкости, а и – векторы-столбцы валовой и конечной продукции соответственно.

Соотношение (7) представляет собой основное балансовое равенство в теории межотраслевого баланса труда. В данном случае его конкретное экономическое содержание заключается в том, что стоимость конечной продукции, оцененной по полным затратам труда, равна совокупным затратам живого труда. Сопоставляя потребительский эффект различных взаимозаменяемых продуктов с полными трудовыми затратами на их выпуск, можно судить о сравнительной эффективности их производства. Показатели полной трудоемкости выявляют структуру затрат на выпуск различных видов продукции, и, прежде всего, соотношение между затратами живого и овеществленного труда.

На основе коэффициентов прямой и полной трудоемкости могут быть разработаны межотраслевые и межпродуктовые балансы затрат труда и использования трудовых ресурсов. Схематически эти балансы строятся по общему типу матричных моделей, однако все показатели в них (межотраслевые связи, конечный продукт, условно чистая продукция и др.) выражены в трудовых измерителях.

5.3. Модель международной торговли

В модели международной торговли процесс взаимных закупок товаров анализируется с использованием понятий собственного числа и собственного вектора матрицы А. Будем полагать, что бюджеты п стран, которые мы обозначим, соответственно, x₁, х₂,..., х_п, расходуются на покупку товаров. Обозначим:

х_i – национальный доход страны i;

а_ij – доля национального дохода страны j, которую она расходует на закупку товаров страны i;

р_i – общая выручка страны от внутренней и внешней торговли.

Предположим, что государство расходует весь свой национальный доход на закупку товаров внутри страны и на импорт из других стран. Это означает, что

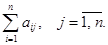
Матрица А, элементами которой являются коэффициенты а_ij, называется структурной матрицей торговли. Сумма элементовкаждого столбца этой матрицы равна единице.

Предположим, что в течение некоторого фиксированного промежутка времени не меняется структура международной торговли (т.е. структурная матрица торговли остается постоянной), тогда как национальные доходы торгующих стран могут измениться. Требуется определить, какими могут быть национальные доходы, чтобы международная торговля осталась сбалансированной, т.е. чтобы сумма платежей всех государств была равна суммарной выручке от внешней и внутренней торговли.

Для любой страны выручка от внутренней и внешней торговли составит

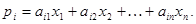
В сбалансированной системе международной торговли не должно быть дефицита, т.е. у каждой страны выручка от торговли должна быть не меньше ее национального дохода: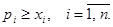

Последнее неравенство справедливо только в случае, когда 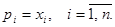т.е. у всех торгующих стран выручка от внешней и внутренней торговли должна совпадать с национальным доходом. В матричной записи это означает, что имеет место равенство: 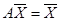, где А – структурная матрица международной торговли, а Х – вектор национальных доходов.

Вектор Х является собственным вектором структурной матрицы торговли А, а соответствующее собственное значение равно единице. Отсюда следует, что баланс в международной торговле будет достигнут, если собственное значение структурной матрицы международной торговли равно единице, а вектор национальных доходов торгующих стран является собственным вектором, отвечающим этому единичному собственному значению.

Пример 6. Требуется найти национальные доходы Х₁, Х₂, Х_з торгующих стран в сбалансированной системе международной торговли. Структурная матрица торговли трех стран имеет вид

.

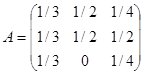Решение. Найдем собственный вектор Х, отвечающий собственному значению λ = 1, решив уравнение (А - λ Е) = 0. Система уравнений имеет вид

.

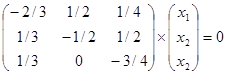С помощью метода Жордана-Гаусса найдем общее решение этой системы

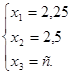
Из приведенных вычислений следует, что сбалансированность торговли трех стран достигается при векторе национальных доходов Х = (2,25 с; 2,5 с; с), т.е. при соотношении национальных доходов стран 2,25:2,5:1, или 9:10:4.

5.4. Модель Неймана

Модель Неймана является обобщенной моделью Леонтьева, поскольку допускает производство одного продукта разными способами (в модели Леонтьева каждая отрасль производит один продукт и никакая другая отрасль не может производить этот продукт).

В модели представлено п продуктов и т способов их производства, каждый способ j задается вектором-столбцом затрат a_j и вектором-столбцом выпусков b_j в расчете на единицу интенсивности процесса

, .

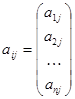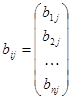Из векторов затрат и выпуска образуются матрицы затрат и выпуска

А = (a₁, a₂, …, a_m), В = (b₁, b₂,..., b_m).

Коэффициенты затрат a_ij и выпуска b_ij неотрицательны. Предположим, что для реализации любого процесса необходимы затраты хотя бы одного продукта, т.е. для каждого j найдется хотя бы одно i, такое что

a_ij > 0, (31)

и каждый продукт может быть произведён хотя бы одним способом, т.е. для каждого i существует некоторое j, такое что

b_ij >0. (32)

Из (31) и (32) следует, что каждый столбец матрицы А и каждая строка матрицы В должны иметь по крайней мере один положительный элемент.

Обозначим через x_t неотрицательный вектор-столбец интенсивности производственных процессов

,

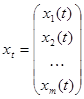а через р_t – вектор-строку неотрицательных цен p_t = (p ₁ (t), p ₂ (t),…, p_m(t)).

Вектор у_t = А x_t – это вектор затрат при заданном векторе интенсивности процессов x_t, а вектор z_t = B x_t – вектор выпусков.

Модель Неймана описывает замкнутую экономику в том смысле, что для производства продукции в следующем производственном цикле, т.е. в год (t –1):

А х_t ≤ В х_t_- ₁, x_t > 0, 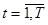. (32)

При этом предполагается, что задан первоначальный вектор запасов В х₀ ≥ 0, В х₀ ≠ 0. Система (32) – это модель Неймана в натуральной форме.

6. Экономические модели и статистические методы

Основы математической статистики

Статистические методы являются составной частью эконометрики – науки, изучающей экономические явления с количественной точки зрения. Эконометрика устанавливает и исследует количественные закономерности в экономике на основе методов теории вероятности и математической статистики, адаптированных к обработке экономических данных.

Закономерности в экономике выражаются в виде связей и зависимостей экономических показателей, математических моделей их поведения. Такие зависимости и модели могут быть получены только путем обработки реальных статистических данных, с учетом внутренних механизмов связи и случайных факторов.

Эконометрический анализ дает возможность обосновать и уточнить форму зависимостей в рассматриваемых макроэкономических моделях, лучше понять механизмы взаимосвязи макроэкономических показателей. Основным элементом экономического исследования является анализ и построение взаимосвязей экономических переменных. Изучение таких взаимосвязей осложнено тем, что они, особенно в макроэкономике, не являются строгими функциональными зависимостями. Во-первых, всегда очень трудно определить все основные факторы, влияющие на данную переменную. Во-вторых, многие такие воздействия носят случайный характер, т.е. содержат случайную составляющую.

Любое эконометрическое исследование всегда предполагает объединение теории (экономической модели) и практики (статистических данных).

Целью сбора экономических данных является получение информационной базы для принятия решений. Анализ данных и принятие решения проводится на основе какой-либо интуитивной (неявной) или количественной (явной) экономической модели.

Использование инструментов Пакета анализа

В пакете Excel помимо мастера функций имеется набор более мощных инструментов для работы с несколькими выборками и углубленного анализа данных, называемый Пакет анализа, который может быть использован для решения задач статистической обработки выборочных данных.

Для установки раздела Анализ данных в пакете Excel сделайте следующее:

- в меню Сервис выберите команду Надстройки;

- в появившемся списке установите флажок Пакет анализа.

Ввод данных. Исследуемые данные следует представить в виде таблицы, где столбцами являются соответствующие показатели. При создании таблицы Excel формация вводится в отдельные ячейки. Совокупность ячеек, содержащих анализируемые данные, называется входным диапазоном. Необходимо соблюдать последовательность обработки данных. Для использования статистического пакета анализа данных следует:

- указать курсором мыши на пункт меню Сервис и щелкнуть левой кнопкой мыши;

- в раскрывающемся списке выбрать команду Анализ данных (если команда Анализ данных отсутствует в меню Сервис, то необходимо установить в Excel пакет анализа данных);

- выбрать необходимую строку в появившемся списке Инструменты анализа;

- ввести входной и выходной диапазоны и выбрать необходимые параметры.

Нахождение основных выборочных характеристик. Для определения характеристик выборки используется процедура Описательная статистика. Процедура позволит получить статистический отчет, содержащий информацию о центральной тенденции и изменчивости входных данных. Для выполнения процедуры необходимо:

- выполнить команду Сервис → Анализ данных;

- в появившемся списке Инструменты анализа выбрать строку Описательная статистика и нажать кнопку ОК (рис. 35);

Рис. 35. Окно выбора метода обработки данных

- в появившемся диалоговом окне указать входной диапазон, то есть ввести ссылку на ячейки, содержащие анализируемые данные. Для этого следует навести указатель мыши на левую верхнюю ячейку данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к правой нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

- указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной диапазон (навести указатель мыши и щелкнуть левой клавишей), далее навести указатель мыши в поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши;

- в разделе Группировка переключатель установить в положение по столбцам;

- установить флажок в поле Итоговая статистика;

- нажать кнопку ОК.

В результате анализа в указанном выходном диапазоне для каждого столбца данных выводятся следующие статистические характеристики: среднее, стандартная ошибка (среднего), медиана, мода, стандартное отклонение, дисперсия выборки, эксцесс, асимметричность, интервал, минимум, максимум, сумма, счет, наибольшее, наименьшее, уровень надежности.

6.1. Проверка статистических гипотез

Помимо описательной статистики важной областью является также аналитическая статистика. Как уже указывалось в разделе «Понятие математической статистики», аналитическая статистика, или теория статистических выводов, ориентирована на обработку данных, полученных в ходе эксперимента, с целью формулировки выводов, имеющих прикладное значение. Здесь решается вопрос, отражают ли наблюдаемые данные объективно существующую реальность. Указанный вопрос решается проверкой соответствующих статистических гипотез. При этом могут выявляться достоверности различий между выборками, взаимосвязи между выборками, влияющие факторы и т.п.

Принятие статистических решений

Статистическая гипотеза – это предположение о виде или отдельных параметрах распределения вероятностей, которое подлежит проверке на имеющихся данных.

Проверка статистических гипотез – это процесс формирования решения о возможности принять или отвергнуть утверждение (гипотезу), основанный на информации, полученной из анализа выборки. Методы проверки гипотез называются критериями.

В большинстве случаев рассматривают так называемую нулевую гипотезу (нуль-гипотезу Н₀), состоящую в том, что все события произошли случайно, естественным образом. Альтернативная гипотеза (Н₁) состоит в том, что события случайным образом произойти не могли, и имело место воздействие некого фактора.

Обычно нулевая гипотеза формулируется таким образом, чтобы на основании эксперимента или наблюдений ее можно было отвергнуть с заранее заданной вероятностью ошибкиα. Эта заранее заданная вероятность ошибки называется уровнем значимости.

Уровень значимости – максимальное значение вероятности появления события, при котором событие считается практически невозможным. В статистике наибольшее распространение получил уровень значимости, равный α = 0,05. Поэтому если вероятность, с которой интересующее событие может произойти случайным образом р < 0,05, то принято считать это событие маловероятным, и если оно все же произошло, то это не было случайным. В наиболее ответственных случаях, когда требуется особая уверенность в достоверности полученных результатов, надежности выводов, уровень значимости принимают равным α = 0,01 или даже α = 0,001.

Величину Р, равную 1- α, называют доверительной вероятностью (уровнем надежности), то есть вероятностью, признанной достаточной для того, чтобы уверенно судить о принятом статистическом решении. Соответственно, в качестве доверительных вероятностей выбирают значения 0,95, 0,99 и 0,999. Интервал, в котором с заданной доверительной вероятностью Р = 1-α находится оцениваемый параметр, называется доверительным интервалом. В соответствии с доверительными вероятностями на практике используются 95-, 99-, 99,9%-ные доверительные интервалы. Граничные точки доверительного интервала называют доверительными пределами.

Выбор того или иного уровня значимости, выше которого результаты отвергаются как статистически не подтвержденные, или, соответственно, доверительной вероятности, в общем случае является произвольным. Окончательное решение зависит от исследователя, традиций и накопленного практического опыта в данной области исследований.

Анализ одной выборки

Анализ однородности выборки. Одним из важных вопросов, возникающих при анализе выборки, является вопрос: относится та или иная варианта к данной статистической совокупности? Решение вопроса не представляет сложности, если распределение в этой совокупности является нормальным. Для этого достаточно использовать правило трех сигм. Согласно этому правилу в пределах М ± 3σ находится 99,7% всех вариант. Поэтому если варианта попадает в этот интервал, то она считается принадлежащей к данной совокупности. Если не попадает, то она может быть отброшена. Хотя этот метод и предполагает нормальность исходного распределения, на практике он успешно работает и может быть использован в большинстве других случаев.

При числе элементов в выборке п < 30 способ более точного определения границ доверительного интервала рассчитан по формуле

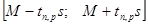, (39)

где М – среднее значение;

s – стандартное отклонение;

t_n_,_p – табличное значение распределения Стьюдента с числом степеней свободы п и доверительной вероятностью р.

Построение доверительных интервалов для среднего. Еще одной важной задачей, возникающей при анализе одной выборки, является сравнение выборочного среднего арифметического со средним значением генеральной совокупности. Эта задача решается с помощью статистических критериев. При этом выясняется, значимо ли отличие выборочного среднего значения от среднего значения генеральной совокупности, из которой предположительно взята выборка, или наблюдаемое различие является случайным.

Действительно, средние значения, получаемые по выборочным данным, обычно не совпадают с генеральным средним (математическим ожиданием). В связи с этим возникает вопрос: можно ли по результатам выборочной оценки судить о свойствах всей генеральной совокупности?

Поскольку каждую оценку, полученную в отдельной выборке, можно рассматривать как случайную величину, то при увеличении числа выборок распределение отдельных оценок будет принимать характер нормального распределения. Это значит, что в случае средних арифметических значения выборочных средних относительно генерального среднего распределяются по нормальному закону, то есть так же как относительные отклонения нормально распределенных вариант от среднего арифметического выборки.

Отсюда, в частности, следует, что 68,3% всех выборочных средних находятся в пределах ∆ = М ± т, где ∆ – предельная ошибка выборки, М – среднее выборочное, m – стандартное отклонение среднего значения. Иными словами, имеется вероятность 0,683, что выборочное среднее отличается от генерального не более, чем на ± m. Здесь 0,683 – доверительная вероятность,

1 – 0,683 = 0,317 – уровень значимости α, ∆ = М ± т – 68%-ный доверительный интервал.

Для принятой в большинстве исследований доверительной вероятности 0,95 доверительный интервал для средних при достаточно большом числе наблюдений (n > 30) примерно равен ± 2 т. При доверительной вероятности 0,99, доверительный интервал составит примерно ± 3 т. Дляболее точного определения границ доверительного интервала можно воспользоваться формулой

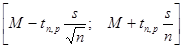, (40)

где М – среднее значение;

s – стандартное отклонение;

t_n_,_p – табличное значение распределения Стьюдента с числом степеней свободы п и доверительной вероятностью p;

п – количество элементов в выборке.

В MS Excel для более точного вычисления границ доверительного интервала и при числе элементов в выборке п < 30 можно воспользоваться функцией ДОВЕРИТ или процедурой Описательная статистика.

Функция ДОВЕРИТ (альфа;станд_откл;размер) определяет полуширину доверительного интервала и содержит следующие параметры:

- Альфа – уровень значимости, используемый для вычисления доверительной вероятности. Доверительная вероятность равняется 100*(1 – альфа) % процентам, или, другими словами, альфа, равное 0,05, означает 95%-ный уровень доверительной вероятности;

- Станд_откл – стандартное отклонение генеральной совокупности для интервала данных, предполагается известным;

- Размер – это размер выборки.

Пример 1. Найти границы 95%-ного доверительного интервала для среднего значения, если у 25 телефонных аккумуляторов среднее время разряда в режиме ожидания составило 140 часов, а стандартное отклонение — 2,5 часа.

Решение:

1. Откройте новую рабочую таблицу. Установите табличный курсор в ячейку А1.

2. Для определения границ доверительного интервала необходимо на панели инструментов Стандартная нажать кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию ДОВЕРИТ, после чего нажмите кнопку ОК.

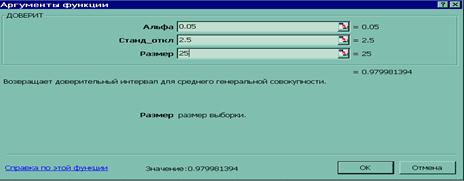
Рис. 36. Пример заполнения диалогового окна ДОВЕРИТ

3. В рабочие поля появившегося диалогового окна ДОВЕРИТ с клавиатуры введите условия задачи: Альфа равна 0,05; Станд_откл – 2,5; Размер – 25 (рис. 36). Нажмите кнопку ОК.

4. В ячейке А1 появится полуширина 95%-ного доверительного интервала для среднего значения выборки – 0,979981. Другими словами, с 95%-ным уровнем надежности можно утверждать, что средняя продолжительность разряда аккумулятора составляет 140 ± 0,979981 часа, или от 139,02 до 140,98 часа.

Использование инструмента Пакет анализа для выявления различий между выборками

Для анализа двух выборок с помощью t -теста Стьюдента могут быть использованы следующие процедуры: Парный двухвыборочный t -тест для средних; Двухвыборочный t -тест с одинаковыми дисперсиями и Двухвыборочный t -тест с различными дисперсиями. В общем случае необходимо воспользоваться процедурой Двухвыборочный t -тест с различными дисперсиями, так как процедуры Парный двухвыборочный t -тест для средних и Двухвыборочный t -тест с одинаковыми дисперсиями относятся к частным, специальным случаям.

Для выполнения процедуры анализа необходимо:

- выполнить команду Сервис → Анализ данных;

- в появившемся списке Инструменты анализа выбрать строку Двухвыборочный t-тест с различными дисперсиями, щелкнуть левой кнопкой мыши и нажать кнопку ОК;

- в появившемся диалоговом окне указать Интервал переменной 1, то есть ввести ссылку на первый диапазон анализируемых данных, содержащий один столбец данных. Для этого следует навести указатель мыши на верхнюю ячейку первого столбца данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

- указать Интервал переменной 2, то есть ввести ссылку на второй диапазон анализируемых данных, содержащий один столбец данных. Для этого следует навести указатель мыши в поле ввода Интервал переменной 2 и щелкнуть левой кнопкой мыши, затем навести указатель мыши на верхнюю ячейку второго столбца данных, нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши;

- указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить флажок в левое поле Выходной диапазон (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной диапазон и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные;

- нажать кнопку ОК.

Результаты анализа. В выходной диапазон будут выведены: средняя, дисперсия и число наблюдений для каждой переменной, гипотетическая разность средних, df (число степеней свободы), значение t -статистики, Р(Т<= t) одностороннее, t критическое одностороннее, Р(Т<= t) двухстороннее, t критическое двухстороннее.

Интерпретация результатов. Если величина вероятности случайного появления анализируемых выборок (P(T<=t) двухстороннее) меньше уровня значимости (α = 0,05), принято считать, что различия между выборками не случайные, то есть различия достоверные.

Пример 7. Рассматривается заработная плата основных групп работников агропромышленной компании: обслуживающего персонала и работников низшего звена.

Можно ли по этим данным сделать вывод о большей зарплате работников низшего звена?

Персонал Работники низшего звена

Решение. Для решения задач такого типа используются так называемые критерии различия, в частности, t -критерий Стьюдента.

1. Введите данные: для персонала – в диапазон А1:А8; работников ресторана – в диапазон В1:В6.

2. Выбор процедуры осуществляется из трех вариантов t- теста. Поскольку данные не имеют попарного соответствия, число их различно, и говорить о равенстве дисперсий затруднительно, выберите процедуру Двухвыборочный t-тест с различными дисперсиями.

Для реализации процедуры в пункте меню Сервис выберите строку Анализ данных и далее укажите курсором мыши на строку Двухвыборочный t-тест с различными дисперсиями.

3. В появившемся диалоговом окне задайте Интервал переменной 1. Для этого наведите указатель мыши на верхнюю ячейку столбца (А1), нажмите левую кнопку мыши и, не отпуская ее, протяните указатель мыши к нижней ячейке (А8), затем отпустите левую кнопку мыши.

4. Аналогично укажите Интервал переменной 2, то есть введите ссылку на диапазон второго столбца В1:В6.

5. Далее укажите выходной диапазон. Для этого поставьте переключатель в положение выходной диапазон (наведите указатель мыши и щелкните левой кнопкой), затем наведите указатель мыши на правое поле ввода выходной диапазон и, щелкнув левой кнопкой мыши, указатель мыши наведите на левую верхнюю ячейку выходного диапазона (С1).Щелкните левой кнопкой мыши и нажмите кнопку ОК.

Результаты анализа. В выходном диапазоне С1:Е13 появятся результаты процедуры Двухвыборочный t-тест с различными дисперсиями (рис. 37).

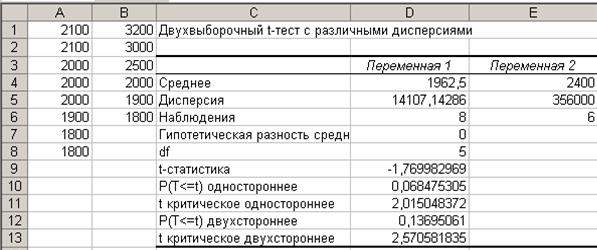
Рис. 37. Исходные данные (А1:В8) и результаты анализа (С1:Е13)

Интерпретация результатов. Средние значения заработной платы (1962 руб. – для персонала и 2400 руб. – для работников низшего звена) довольно сильно отличаются. Тем не менее нулевая гипотеза о том, что разницы между группами нет (то средние выборок равны между собой), отвергнута быть не может. Это следует из того, что вероятность реализации нулевой гипотезы достаточно велика (р = 0,1389, что больше, чем уровень значимости 0,05, то есть р > 0,05) и величина вероятности случайного появления анализируемых выборок (Р(Т<=t) двухстороннее) больше уровня значимости (α = 0,05). А это позволяет говорить, что различия между выборками могут быть случайными, то есть различия недостоверные.

Таким образом, из полученных результатов исследования вытекает, что на основании приведенных данных нельзя сделать вывод о достоверно большей зарплате работников низшего звена.

6.2. Дисперсионный анализ

В случае необходимости оценить достоверность различия между несколькими группами наблюдений (выборками) используют методы дисперсионного анализа.

Дисперсионный анализ предназначен для исследования задачи о действии на измеряемую случайную величину (отклик) одного или нескольких независимых факторов, имеющих несколько градаций. Причем в однофакторном, двухфакторном и т.д. анализе влияющие на результат факторы считаются известными, и речь идет только о выяснении существенности или оценке этого влияния.

Применение дисперсионного анализа возможно, если можно предполагать соответствие выборочных групп генеральным совокупностям с нормальным распределением и независимость распределений наблюдений в группах.

В дальнейшем ограничимся рассмотрением простейшего случая дисперсионного анализа – однофакторного анализа. При этом задача заключается в том, чтобы сравнить дисперсию, обусловленную случайными причинами, с дисперсией, вызываемой наличием исследуемого фактора. Если они значимо различаются, то считают, что фактор оказывает статистически значимое влияние на исследуемую переменную. Значимость различий проверяется по критерию Фишера.

Влияние случайной составляющей характеризуют внутригрупповая дисперсия, а влияние изучаемого фактора – межгрупповая. Внутригрупповая дисперсия рассчитывается по формуле:

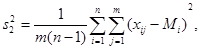(41)

межгрупповая:

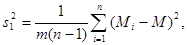(42)

где М – общее среднее: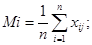

т – количество групп;

п – количество элементов в группе.

В MS Excel для проведения однофакторного дисперсионного анализа используется процедура Однофакторный дисперсионный анализ.

Для проведения дисперсионного анализа необходимо:

- ввести данные в таблицу, так чтобы в каждом столбце оказались данные, соответствующие одному значению исследуемого фактора, а столбцы располагались в порядке возрастания (убывания) величины исследуемого фактора;

- выполнить команду Сервис → Анализ данных;

- в появившемся диалоговом окне Анализ данных в списке Инструменты анализа выбрать процедуру Однофакторный дисперсионный анализ, указав курсором мыши и щелкнув левой кнопкой мыши. Затем нажать кнопку ОК;

- в появившемся диалоговом окне задать Входной интервал, то есть ввести ссылку на диапазон анализируемых данных, содержащий все столбцы данных. Для этого следует навести указатель мыши на верхнюю левую ячейку диапазона данных нажать левую кнопку мыши и, не отпуская ее, протянуть указатель мыши к нижней правой ячейке, содержащей анализируемые данные, затем отпустить левую кнопку мыши (рис. 38);

- в разделе Группировка переключатель установить в положение по столбцам;

- указать выходной диапазон, то есть ввести ссылку на ячейки, в которые будут выведены результаты анализа. Для этого следует поставить переключатель в положение Выходной интервал (навести указатель мыши и щелкнуть левой кнопкой), далее навести указатель мыши на правое поле ввода Выходной интервал и щелкнуть левой кнопкой мыши, затем указатель мыши навести на левую верхнюю ячейку выходного диапазона и щелкнуть левой кнопкой мыши. Размер выходного диапазона будет определен автоматически, и на экран будет выведено сообщение в случае возможного наложения выходного диапазона на исходные данные;

- нажать кнопку ОК.

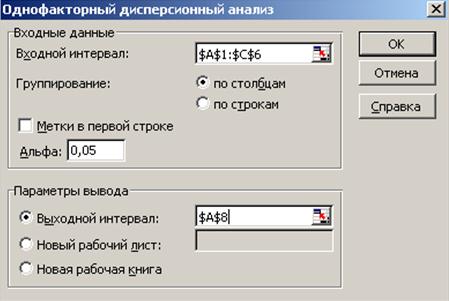
Рис. 38. Пример заполнения окна Однофакторный дисперсионный анализ

Результаты анализа. Выходной диапазон будет включать в себя результаты дисперсионного анализа: средние, дисперсии, критерий Фишера и другие показатели.

Интерпретация результатов. Влияние исследуемого фактора определяется по величине значимости критерия Фишера, которая находится в таблице Дисперсионный анализ на пересечении строки Между группами и столбца Р-Значение. В случаях, когда Р-Значение < 0,05, критерий Фишера значим и влияние исследуемого фактора можно считать доказанным.

Кроме рассмотренной процедуры однофакторного дисперсионного анализа, для проведения двухфакторного дисперсионного анализа в пакете анализа реализованы процедуры Двухфакторный дисперсионный анализ с повторениями и Двухфакторный дисперсионный анализ без повторений.

6.3. Корреляционный анализ

Корреляционный анализ служит для выявления взаимосвязей между выборками.

Коэффициент корреляции

Знание взаимозависимостей отдельных признаков дает возможность решать одну из кардинальных задач любого научного исследования: возможность предвидеть, прогнозировать развитие ситуации при изменении конкретных характеристик объекта исследования. Например, основное содержание любой экономической политики в конечном счете может быть сведено к регулированию экономических переменных, осуществляемому на базе выявленной тем или иным образом информации об их взаимовлиянии. Поэтому проблема изучения взаимосвязей показателей различного рода является одной из важнейших в статистическом анализе.

Обычно взаимосвязь между выборками носит не функциональный, а вероятностный (или стохастический) характер. В этом случае нет строгой однозначной зависимости между величинами. При изучении стохастических зависимостей различают корреляцию и регрессию.

Регрессионный анализ устанавливает формы зависимости между случайной величиной Y и значениями одной или нескольких переменных величин.

Корреляционный анализ состоит в определении степени связи между двумя случайными величинами Х и Y. В качестве меры такой связи используется коэффициент корреляции. Коэффициент корреляции оценивается по выборке объема n связанных пар наблюдений (x_i, y_i) из совместной генеральной совокупности Х и Y.

Существует несколько типов коэффициентов корреляции, применение которых зависит от предположений о совместном распределении величин Х и Y.

Для оценки степени взаимосвязи наибольшее распространение получил коэффициент линейной корреляции (Пирсона), предполагающий нормальный закон распределения наблюдений.

Коэффициент корреляции (R, r) – параметр, характеризующий степень линейной взаимосвязи между двумя выборками. Коэффициент корреляции изменяется от -1 (строгая обратная линейная зависимость) до 1 (строгая прямая пропорциональная зависимость). При значении 0 линейной зависимости между двумя выборками нет. Здесь под прямой зависимостью понимают ту, при которой увеличение или уменьшение значения одного признака ведет, соответственно, к увеличению или уменьшению второго. Например, при увеличении температуры возрастает давление газа, а при уменьшении – снижается (при постоянном объеме). При обратной зависимости увеличение одного признака приводит к уменьшению второго и наоборот. Примером обратной корреляционной зависимости может служить связь между температурой воздуха на улице и количеством топлива, расходуемого на обогрев помещения.

На практике коэффициент корреляции принимает некоторые промежуточные значения между 1 и -1. Для оценки степени взаимосвязи можно руководствоваться следующими эмпирическими правилами. Если коэффициент корреляции (r) по абсолютной величине (без учета знака) больше, чем 0,95, то принято считать, что между параметрами существует практически линейная зависимость (прямая – при положительном r и обратная – при отрицательном r). Если коэффициент корреляции | r | лежит в диапазоне от 0,8 до 0,95, говорят о сильной степени линейной связи между параметрами. Если 0,6 < | r | < 0,8, говорят о наличии линейной связи между параметрами. При | r | < 0,4 обычно считают, что линейную взаимосвязь между параметрами выявить не удалось.

В MS Excel для вычисления парных коэффициентов линейной корреляции используется специальная функция КОРРЕЛ. Параметры функции КОРРЕЛ (масcuв 1; мaccuв 2), где: массив 1 – это диапазон ячеек первой случайной величины; массив 2 – это второй интервал ячеек со значениями второй случайной величины.

Пример 8. Имеются результаты семимесячных наблюдений реализации минеральных удобрений вида А и вида В.

Месяц Вид удобрения А Вид удобрения В

Необходимо определить, имеется ли взаимосвязь между количеством продаж удобрений обоих видов.

Решение. Для выявления степени взаимосвязи прежде всего необходимо ввести данные в рабочую таблицу. Откройте новую рабочую таблицу. Введите в ячейку А1 слова Вид удобрения А. Затем в ячейки А2:А8 – соответствующие значения числа продаж.

В ячейки В1:В8 введите название и значения для Вид удобрения В. Затем вычисляется значение коэффициента корреляции между выборками. Для этого табличный курсор установите в свободную ячейку (А9). На панели инструментов нажмите кнопку Вставка функции (f_x). В появившемся диалоговом окне Мастер функций выберите категорию Статистические и функцию КОРРЕЛ, после чего нажмите кнопку ОК. Появившееся диалоговое окно КОРРЕЛ з