Элементарные случайные процессы

Как уже отмечалось, случайный процесс в результате опыта превращается на некотором интервале от t = t ₀ до t = t ₀ + q в неслучайную функцию времени, которая называется реализацией случайного процесса на этом интервале. В общем случае (даже если характеристики случайного процесса известны) мы не можем точно предсказать, как будет развиваться случайный процесс в будущем при t > (t ₀ + q) если опыт еще не завершен. Однако существует класс простейших случайных процессов, для которых можно точно сказать, как будет выглядеть данная реализация при дальнейшем продолжении опыта. Такие случайные процессы называются элементарнымислучайными процессами.

Элементарным случайным процессом (э. с. п.) будем называть такую функцию аргумента t, для которой зависимость от t представлена обычной неслучайной функцией, в которую в качестве аргумента входит одна или несколько обычных случайных величин.

То есть, в каждой реализации элементарного случайного процесса случайная величина является константой, или другими словами – каждая случайная константа порождает свою реализацию.

В качестве примера рассмотрим э. с. п. Y (t):

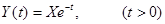, (6.34)

где X – положительная непрерывная случайная величина. Семейство реализаций э. с. п. Y (t) показано на рис.6.6.

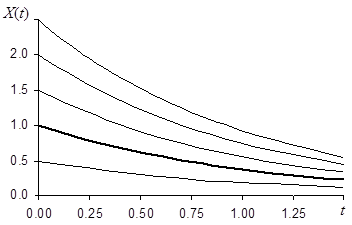
Рис.6.6. Семейство реализаций элементарного случайного процесса .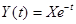

Каждая их реализаций представляет собой кривую с ординатами, пропорциональными кривой e^–t (жирная линия); отдельные реализации (тонкие линии) различаются между собой масштабом по оси ординат.

Заметим, что хотя данный процесс довольно прост по структуре, он не является стационарным.

С некоторой натяжкой модель данного э. с. п. можно использовать для описания ветви спада половодья. Если предположить, что в некотором створе ветвь спада половодья является устойчивой и существенно не искажается осадками в течение, допустим, двух месяцев после прохождения максимума, то ее можно аппроксимировать выражением:

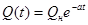, (6.35)

где a – районный параметр (a > 0); Q _н – расход воды в начальный момент времени t = t ₀.

В качестве t ₀ следует принять постоянную дату, более позднюю, чем дата самого позднего из всех наблюденных максимумов половодья. Тогда выражение (6.35) можно трактовать как элементарный случайный процесс, где a – неслучайная величина, Q _н – случайная величина из интервала (0, ∞), представляющая собой расход воды в i -том году на дату t ₀.

В качестве функции распределения Q _н можно использовать, например, кривую Крицкого-Менкеля, а ее параметры оценить по эмпирическим данным.