Примеры машин Тьюринга

Рассмотрим машины Тьюринга, реализующие и обеспечивающие формирование рекурсивных функций.

Пример 1. Построить машину Тьюринга, вычисляющую функцию .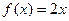

Пусть алфавит машины Тьюринга состоит из двух символов {0, 1}, где 0 – пустой символ, а 1 – символ занятой ячейки. В этом алфавите любое целое неотрицательное число k представляется k+1 символами 1, записанными в соседних ячейках ленты. В этом случая число 0 будет записано так …010…

Определим порядок вычисления значения этой функции машиной Тьюринга. Так как результат должен представлять массив из 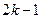занятых ячеек, где 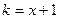- число ячеек, занятых аргументом x, то вычисление организуем следующим образом. В ячейку, занятую аргументом x, вместо символа 1 записываем пустой символ 0. В каждом таком случае символ 1 записывается в двух ячейках, представляющих результат. Этот результат формируем в виде массива ячеек, расположенных справа от массива ячеек, занятых аргументом x, через одну пустую ячейку. Когда вместо всех ячеек, занятых аргументом x, будут только пустые ячейки, в новом массиве занятых ячеек удаляется одна ячейка с символом 1.

Программа работы машины Тьюринга, вычисляющая функцию 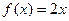, имеет вид:

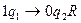- удалена одна занятая ячейка аргумента.

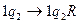- читаются занятые ячейки аргумента.

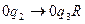- найдена разделяющая пустая ячейка.

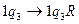- читаются занятые ячейки результата.

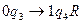- заполнена одна пустая ячейка результата.

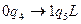- заполнена вторая ячейка результата.

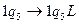- просматриваются в обратном порядке занятые ячейки результата.

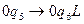- найдена пустая разделяющая ячейка.

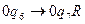- найдена вторая пустая ячейка.

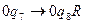- снова читается пустая разделительная ячейка.

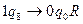- удаляется один занятый символ. Конец.

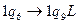- найдена занятая ячейка аргумента.

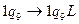- просматриваются в обратном порядке занятые ячейки аргумента.

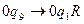- найдена пустая ячейка перед занятыми ячейками аргумента.

Пример 2. Построить машину Тьюринга, применимую ко всем словам 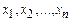в алфавите { a, b } и переводящую их в слово 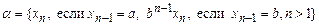. Проверить работу построенной машины над некоторыми словами.

Решение. Опишем работу алгоритма, решающего эту задачу. Вначале с помощью команд 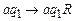, 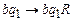проходим до конца слова, не изменяя его символов. Признаком окончания слова будем считывание символа 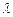в состоянии .

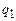С помощью команд 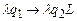, , 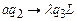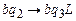движемся влево, не изменяя последнего символа.

Если в состоянии 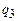считываем символ a, значит, 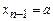, надо стирать все символы слова 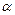, кроме последнего. Это можно сделать с помощью команд , , .

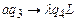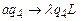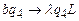Если в состоянии 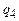считывается символ 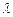, значит, вся работа проделана, и пора останавливаться с помощью команды .

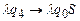Если в состоянии 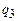считываем символ b, значит, 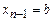, надо все символы, кроме 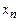, заменить буквами b. Это делаем с помощью команд , , .

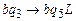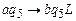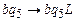Если в состоянии 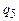считываем символ 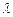, значит, все символы исходного слова пройдены, можно переходить в состояние 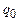с помощью команды .

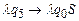Проверим работу построенной машины Тьюринга над словом abba:

abba,	abba,	abba,	abba,	abbal,	abba,	abba,	abba,
lbbba,	lbbba.

Итак, в слове abba предпоследний символ - b, и все буквы исходного слова, кроме последнего, заменены буквой b.

Проверим работу построенной машины Тьюринга над словом bbaaa:

bbaaa	bbaaa	bbaaa	bbaaa	bbaaa	bbaaal	bbaaa
bbaaa	bbala	bblla	bllla	llllla	llllla

В слове bbaaa предпоследний символ - a, и все буквы исходного слова, кроме последнего, заменены пустыми символами .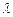

Итак, проверка сделана, результат работы машины Тьюринга удовлетворяет требованиям, которые ставились в условии задачи.

В приведенных примерах показана реализуемость на машинах Тьюринга основных свойств алгоритма: дискретности, детерминированности, массовости и результативности.

Чтобы можно было строить сложные машины Тьюринга, определяют понятие композиции машин Тьюринга.

Композицией машин Тьюринга М₁ и М₂ называется машина Тьюринга М, которая первоначально функционирует как машина Тьюринга М₁, заключительное состояние которой q ₀ изменяют на начальное состояние машины Тьюринга М₂. И далее машина М функционирует как машина Тьюринга М₂.

Композицию машин Тьюринга обозначают: М = М₁ º М₂.

Из определения композиции машин Тьюринга следует, что М₁ º М₂ ≠ М₂ º М₁.

Так, если необходимо построить машину Тьюринга, вычисляющую функцию ƒ(х, у) = х + у + 1, то достаточно выполнить композицию машин Тьюринга. Пусть машина М₁ вычисляет функцию ƒ(х) = х + 1, а машина М₂ вычисляет функцию ƒ(х + у). Тогда машина М = М₁ º М₂ будет вычислять, очевидно, функцию ƒ(х, у) = х + у + 1. Для этого нужно к программе, описывающей машину М₁, присоединить команды машины М₂. Состояния машины М₁ будут также состояниями машины М. Заключительное состояние q ₀ машины М₁ следует заменить состоянием q ₂,которое будет соответствовать начальному состоянию машины М₂. тогда изменится соответствующим образом нумерация состояний машины М₂: состояние q ₁ изменится на состояние q ₂ машины М, состояние q ₂ изменится на состояние q ₃ и так далее.

Существует много модификаций машин Тьюринга, среди которых можно выделить универсальные и многоленточные машины. Для универсальных машин характерно одновременное использование правой и левой полулент, на одной из которых записываются все команды для вычисления заданной функции, а на другой все текущие конфигурации.

Для многоленточных машин характерно наличие нескольких лент и нескольких головок, что позволяет организовать одновременную работу согласно протоколу на всех лентах, что удобно при организации сложных параллельных вычислений.

Рекурсивные функции и машины Тьюринга дают косвенное определение понятие алгоритма: если возможно доказать, что некоторая функция примитивно-рекурсивна, или возможно построение машины Тьюринга для получения решения некоторой задачи, то такая задача разрешима.

С другой стороны, если доказано, что решение некоторой задачи не может быть получено вычисление примитивно-рекурсивных функций, или доказано, что для решения данной задачи не может быть построена машина Тьюринга, то такая задача называется алгоритмически неразрешимой.

Важность доказательства факта, что некоторая задача алгоритмически неразрешима, состоит в том, что исследователь не будет тратить время и силы на разработку алгоритма решения данной задачи в общем виде.