Кривые линии и их проекции

Кривая линия это геометрический образ, который может рассматриваться как геометрическое место последовательных положений непрерывно перемещающейся в пространстве точки. Кривые линии могут быть также границами поверхностей или представлять результат взаимного пересечения поверхностей.

Если учесть, что положение точки при ее движении по заданной траектории зависит от непрерывно меняющегося параметра – расстояния от точки до начала координат, – то можно утверждать, что положение точки, образующей линию, определяется этим непрерывно меняющимся параметром. Отсюда вытекает, что линия – это непрерывное однопараметрическое множество точек.

Способы образования кривых линий различны. Одни линии образуются по определенному закону (закономерные кривые линии), образование других носит эмпирический (опытный) характер (незакономерные кривые линии).

Закономерные кривые линии можно задать графически и аналитически, то есть уравнением.

Незакономерные кривые линии задают только графически на чертеже.

Закономерные кривые линии разделяют на алгебраические, которые определяются в декартовых координатах алгебраическими уравнениями, и трансцендентные, которые определяются неалгебраическими уравнениями, такие, как синусоида, циклоида, архимедова спираль и др.

В начертательной геометрии кривые линии изучаются по их проекциям. Построение проекций линий существенно зависит от того, принадлежат ли все точки кривой одной плоскости или нет. Если все точки кривой линии принадлежат одной плоскости, то такая кривая называется плоской.

Кривая линия, которая не может быть совмещена с плоскостью всеми своими точками, называется пространственной или линией двоякой кривизны.

Большое значение при рассмотрении плоских алгебраических кривых линий имеет определение порядка кривой. Это определение может быть дано как алгебраически (порядком кривой называется степень ее алгебраического уравнения), так и геометрически (порядком плоской алгебраической кривой называется число точек пересечения кривой с прямой линией). При этом надо иметь в виду, что в число точек пересечения включаются как точки с действительными, так и с мнимыми координатами.

Из свойств параллельного проецирования вытекают свойства кривых линий, которые сохраняются у их проекций:

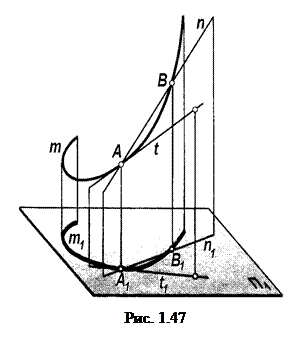
- если точка А принадлежит кривой m (рис. 1.47), то проекция А₁ этой точки принадлежит проекции m₁ кривой;

- секущая n и касательная t к кривой линии проецируются соответственно в секущую n₁ и касательную t₁ к проекции кривой m₁ (рис. 1.47);

- бесконечно удаленные точки кривой линии, например 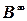, проецируются в бесконечно удаленные точки ее проекции ;

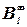- порядок плоской алгебраической кривой при параллельном проецировании не меняется, т. е. сохраняется число точек пересечения кривой и прямой линий.

Сохранение этих свойств кривых при параллельном проецировании позволяет утверждать, что окружность и эллипс проецируются в эллипс, парабола проецируется в параболу, а гипербола в гиперболу.

Кривую линию называют гладкой кривой, если в каждой из ее точек имеется единственная касательная, непрерывно изменяющаяся от точки к точке.

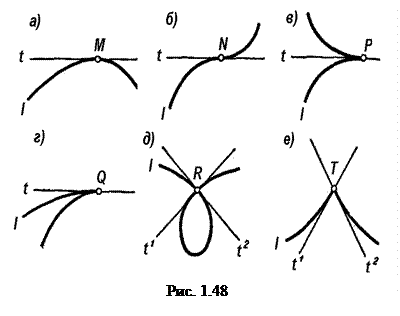
Точки кривых разделяются на обыкновенные и особые. На рис. 1.48, а показана обыкновенная точка М, а на рис. 1.48, б, в, г, д, е –некоторые особые точки: точка перегиба N, точки возврата P первого рода и Q второго рода, узловая точка R и точка излома T. При проецировании сохраняются все эти особенности точек кривой, поэтому по проекции плоской кривой можно судить о характере самой кривой.

Для пространственной кривой судить о характере ее точек возможно лишь при наличии двух проекций кривой. Дело в том, что на проекциях пространственных кривых могут получаться кажущиеся особые точки, отсутствующие в действительности на кривой.

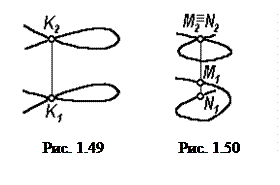
Например, на рис. 1.49 и 1.50 даны проекции двух пространственных кривых, одна из которых имеет действительную двойную точку К(К₁,К₂), а другая – кажущиеся двойные точки М и N.