заранее нельзя уверенно предвидеть, какое из возможных значений примет случайная величина в итоге испытания; это зависит от многих случайных причин, учесть которые невозможно. Казалось бы, поскольку о каждой случайной величине мы располагаем в этом смысле весьма скромными сведениями, то вряд ли можно установить закономерности поведения и суммы достаточно большого числа случайных величин. На самом деле это не так. при некоторых сравнительно широких условиях суммарное поведение достаточно большого числа случайных величин почти утрачивает случайный характер и становится закономерным.
Для практики очень важно знание условий, при выполнении которых совокупное действие очень многих случайных причин приводит к результату, почти не зависящему от случая, так как позволяет предвидеть ход явлений. Эти условия и указываются в теоремах, носящих общее название закона больших чисел. К ним относятся теоремы Чебышева и Бернулли.
Теорема Чебышева. Если X 1, X 2, …,Xn,… – последовательность независимых случайных величин, у каждой из которых есть математическое ожидание M (Xi) = ai и дисперсия 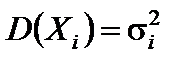
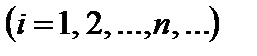 , причем дисперсии ограничены сверху одним и тем же числом С, то для любого положительного числа e выполняется неравенство
, причем дисперсии ограничены сверху одним и тем же числом С, то для любого положительного числа e выполняется неравенство
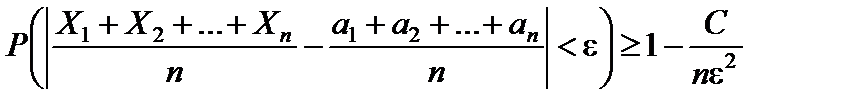 . (6.5)
. (6.5)
Данная теорема называется законом больших чисел в форме Чебышева.
Следствие 1. В неравенстве (6.5) перейдем к пределу при 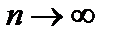 , получим
, получим
 .
.
Но так как вероятность больше единицы не бывает, то
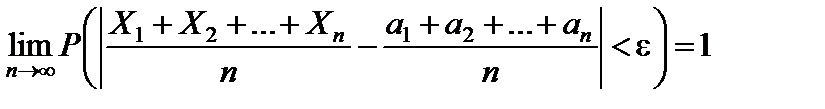 . (6.6)
. (6.6)
Следствие 2. Если X 1, X 2, …,Xn,… – последовательность независимых случайных величин, математические ожидания каждой из которых равны a, а дисперсии – s2, то неравенство (6.5), формула (6.6) соответственно принимают вид
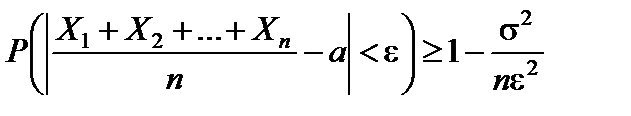 ,
,

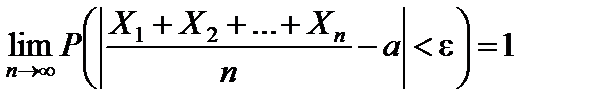 .
.
Данные результаты имеют большое практическое применение. Так, если надо измерить некоторую величину, истинное значение которой равно a, проводят n измерений этой величины. Результат каждого измерения – это случайная величина Xi (i = 1,2,…, n,…). Если при измерениях отсутствует систематическая погрешность, то M (Xi) = a. Можно считать, что Xi – независимая случайная величина, а ее дисперсия ограничена. Тогда справедливо следствие, и, значит, среднее арифметическое значение результатов измерений с ростом n приближается к истинному значению измеряемой величины a. Поэтому можно положить
 .
.
Тест 6.8. Случайные величины X 1, X 2, …,Xn,…, для которых применим закон больших чисел в форме Чебышева должны иметь следующие числовые характеристики:
1) M (Xi) и D (Xi) (i = 1,2,…, n,…), причем математические ожидания ограничены сверху одним и тем же числом 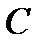 ;
;
2) M (Xi) (i = 1,2,…, n,…), ограниченные сверху одним и тем же числом 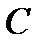 ;
;
3) M (Xi) и D (Xi) (i = 1,2,…, n,…);
4) M (Xi) и D (Xi) (i = 1,2,…, n,…), причем дисперсии ограничены сверху одним и тем же числом 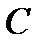 ;
;
5) D (Xi) (i = 1,2,…, n,…).
Пример 6.5. Для определения средней продолжительности горения электроламп в партии из 200 одинаковых ящиков было взято на выборку по одной лампе из каждого ящика. Используя терему Чебышева, оценить вероятность того, что средняя продолжительность горения отобранных 200 электроламп отличается от средней продолжительности горения лампы во всей партии по абсолютной величине меньше, чем на 5 ч, если известно, что дисперсия продолжительности горения любой лампы в каждом ящике меньше 49.
Решение
Пусть Xi – продолжительность горения электролампы, взятой из i -го ящика. По условию D (Xi) < 49. Очевидно, что средняя продолжительность горения лампы в выборке 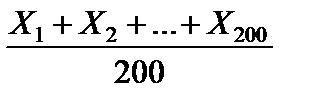 , а средняя продолжительность горения ламп во всей партии
, а средняя продолжительность горения ламп во всей партии 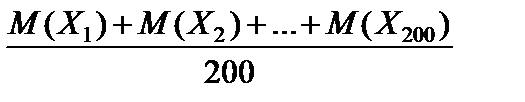 .
.
Оценим сразу вероятность
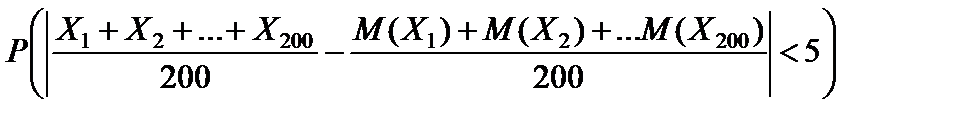 .
.
Это есть левая часть неравенства (6.5). Так как 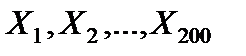 – независимые случайные величины, то эта вероятность оценивается правой частью неравенства (6.5), где следует положить С = 49, e = 5, n = 200.
– независимые случайные величины, то эта вероятность оценивается правой частью неравенства (6.5), где следует положить С = 49, e = 5, n = 200.
Итак, искомая вероятность
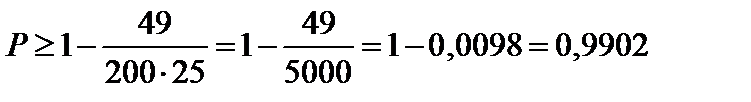 .
.
Ответ: 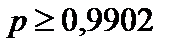 .
.
Тест 6.9. За значение некоторой величины принимают среднее арифметическое достаточно большого числа ее измерений. Известно, что дисперсия возможных результатов каждого измерения не превосходит 25 мм. Оценкой вероятности того, что при 1000 измерениях неизвестной величины отклонение принятого значения от истинного по абсолютной величине не превзойдет 0,5 мм, по теореме Чебышева является выражение:
1) 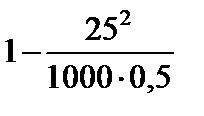 ;
;
2) 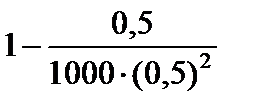 ;
;
3) 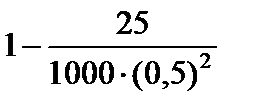 ;
;
4) 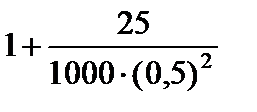 ;
;
5) 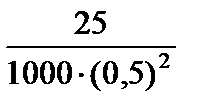 .
.
Тест 6.10. Для определения средней урожайности поля площадью 1800 га взяли на выборку 1 м2 с каждого гектара. Известно, что по каждому гектару поля дисперсия не превышает 6. Оценкой вероятности того, что отклонение средней выборочной урожайности отличается от средней урожайности по всему полю по абсолютной величине меньше, чем на 0,25 ц, по теореме Чебышева является выражение:
1) 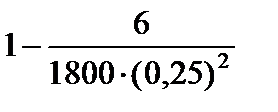 ;
;
2) 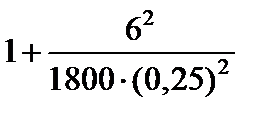 ;
;
3) 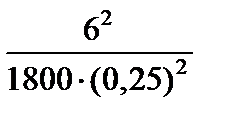 ;
;
4) 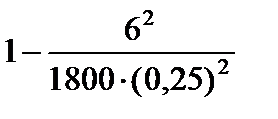 ;
;
5) 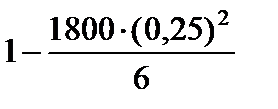 .
.
 2015-04-20
2015-04-20 4034
4034
