Диаграммы сравнения

Различные виды диаграмм применяются для сравнения одноименных статистиче­ских данных, характеризующих разные территории или объекты. Наиболее распростра­нённым видом таких диаграмм являются столбиковые диаграммы. Они представляют собой график, в котором различные величины представлены расположенными в высоту прямоугольниками («столбиками») одинаковой или разной высоты. Столбиковые диаграммы применяются для сравнения некоторых объектов во времени.

Построение такого рода диаграмм требует только одной вертикальной масштаб-вой шкалы, которая определяет высоту каждого столбика.

Масштабная шкала должна начинаться с нуля, быть непрерывной и на ней записываются лишь круглые или округленные значения.

Столбики должны быть даны на некотором, одинаковом для всех расстоянии или вплотную друг к другу. Ширина столбиков берется произвольной. На шкале должна быть указана единица измерения. При выборе масштаба надо рассчитать так, чтобы максимальное число было представлено на графике.

Пример. Требуется изобразить с помощью столбиковой диаграммы данные о тру­доустройстве граждан органами государственной службы занятости региона (цифры условные): в 2004 г. трудоустроено 2822 чел,; в 2003 г. - 2398 чел.; в 2002 г. - 2406 чел.; в

2001 г. - 2218 чел. Примем масштаб: 500 чел. соответствует 1 см. Тогда высота первого столбика (трудоустройство в 2001 г.) будет равна 4,4 см (1 см*2218/500), высота второго ' (в 2002 г.)-4,8 см; высота третьего (в 2003 г.)-4,79 см; высота четвертого (в 2004 г.)-5,6 см.

Наглядность данной диаграммы достигается сравнением высоты столбиков (рис. 4.4).

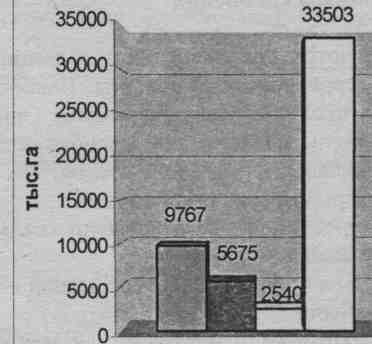
На рис. 4.5 с помощью столбиковой диаграммы показана структура посевных пло­щадей сельхозпредприятий N-ой области РФ за 2004 г. (цифры условные). На этой диаграмме столбики располагаются вплотную по группам объектов в пространстве/

Масштаб принят такой, что каждым 5000 тыс. га соответствует отрезок в 1 см.

Если прямоугольники, изображающие показатели, расположить не по вертикали, а

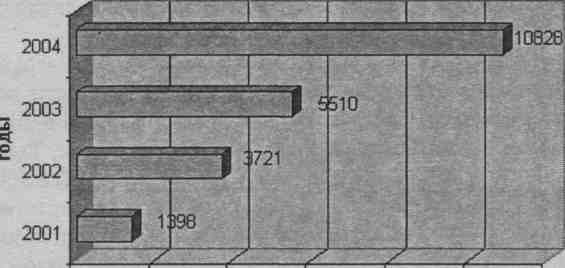
по горизонтали, то диаграмма получит название ленточной. В качестве примера приведем полосовую диаграмму сравнения, характеризующую данные о реализации минеральных удобрений сельхозпредприятиями в N-ом регионе за 2001-2004 гг. (рис. 4.6).

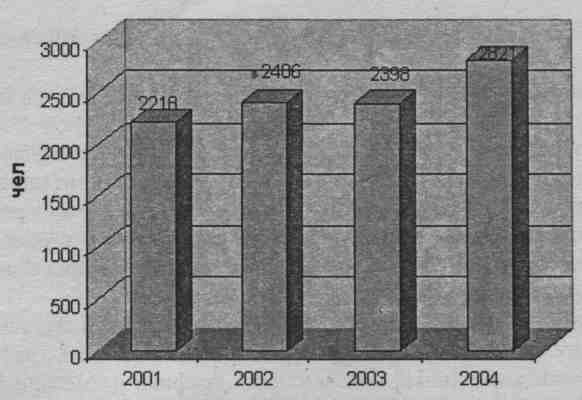Рис. 4.4. Динамика трудоустройства граждан органами государственной службы занятости в регионе за 2001-2004 гг.

Рис. 4.5. Структура посевных площадей сельхозпредприятий N-ой области РФ в 2004г.

0 2000 4000 6000 8000 10000 12000

Тыс.т

Рис. 4.6. Динамика реализации минеральных удобрений сельскохозяйственными предприятиями в N-ом регионе за 2001-2004 гг.

Иногда разница между наименьшими и наибольшими значениями сравниваемых данных настолько велика, что установление подходящего масштаба для столбиков или полос оказывается затруднительным. В этих случаях вместо столбиковой (полосовой) диаграммы целесообразно применить плоскостную (двухмерную) диаграмму - квадрат­ную или круговую. Принцип построения этих диаграмм заключается в том, что величины сравниваемых данных изображаются площадями квадратов или кругов. Иными словами, площади квадратов (кругов) должны быть пропорциональны величинам изображаемых явлений, но сами площади квадратов (кругов) пропорциональны квадратам их сторон (ра­диусов). Следовательно, стороны квадратов или радиусов кругов должны быть пропорциональны корням квадратным из величин изображаемых статистических данных.

Пример. Необходимо с помощью квадратной диаграммы изобразить реализацию

молочных продуктов предприятиями розничной торговли в одном из регионов за 2004 г.

по следующим данным:

Товар	Товарооборот, млн. руб.
творог
сметана
молоко

Для построения квадратной диаграммы сначала извлечем квадратные корни из чи­сел: √11=3,32; √16=4; √19=4,36. Затем установим масштаб, например, примем 1см-1,5 млн. руб. Тогда сторона 1-го квадрата составит 2,2см (3,32:1,5); 2-го - 2,7см; 3-го - 2,9см (4,36:1,5). Далее строим квадраты.

Для правильного построения диаграммы квадраты необходимо расположить на одинаковом расстоянии друг от друга, а в каждой фигурке указать числовое значение, которое она изображает, не приводя масштаба измерения (рис. 4.7).

16

11