Теорема. Если функция  интегрируема на отрезке
интегрируема на отрезке 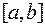 , то она ограничена на этом отрезке.
, то она ограничена на этом отрезке.
Доказательство. Пусть функция  не ограничена на отрезке
не ограничена на отрезке 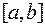 и пусть фиксировано некоторое разбиение
и пусть фиксировано некоторое разбиение
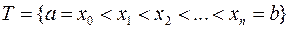
этого отрезка. В силу неограниченности функции  на всем отрезке
на всем отрезке 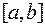 она не ограничена по крайней мере на одном из отрезков разбиения
она не ограничена по крайней мере на одном из отрезков разбиения 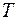 . Пусть для определенности функция
. Пусть для определенности функция  не ограничена на отрезке
не ограничена на отрезке 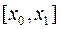 , тогда на этом отрезке существует последовательность точек
, тогда на этом отрезке существует последовательность точек 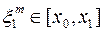 ,
, 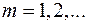 такая,что
такая,что
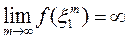
Зафиксируем теперь точки 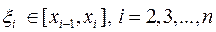 , тогда сумма
, тогда сумма
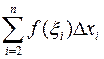
будет иметь вполне определенное значение. Поэтому
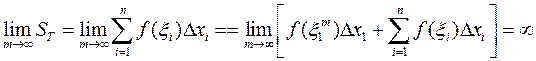 ,
,
и, значит, каково бы ни было число 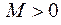 , всегда можно подобрать такой номер
, всегда можно подобрать такой номер 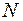 , что если на первом отрезке
, что если на первом отрезке 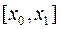 взять точку
взять точку 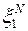 , то
, то 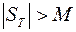 . Отсюда следует, что суммы
. Отсюда следует, что суммы 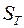 не могут стремиться ни к какому конечному пределу при
не могут стремиться ни к какому конечному пределу при 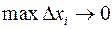 . Теорема доказана.
. Теорема доказана.
Условие ограниченности функции  , являясь необходимым условием интегрируемости функции, не является вместе с тем достаточным для интегрируемости. В качестве примера, доказывающего это утверждение, рассмотрим так называемую ф ункцию Дирихле:
, являясь необходимым условием интегрируемости функции, не является вместе с тем достаточным для интегрируемости. В качестве примера, доказывающего это утверждение, рассмотрим так называемую ф ункцию Дирихле:
|
|
|
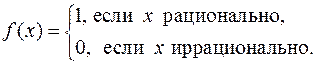
Рассмотрим эту функцию, например, на отрезке 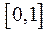 . Она, очевидно, ограничена на этом отрезке. Покажем, что она не интегрируема. Зафиксируем произвольное разбиение
. Она, очевидно, ограничена на этом отрезке. Покажем, что она не интегрируема. Зафиксируем произвольное разбиение 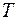 отрезка
отрезка 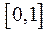 . Если выбрать точки
. Если выбрать точки 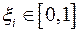 ,
, 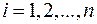 , рациональными, то в этих точках получим
, рациональными, то в этих точках получим
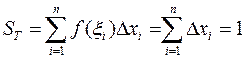
аесли взять 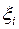 иррациональными, то получим
иррациональными, то получим
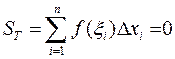
Так как это верно для любого разбиения 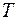 , то интегральные суммы заведомо не стремятся ни к какому пределу при
, то интегральные суммы заведомо не стремятся ни к какому пределу при 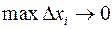 .
.
 2015-05-05
2015-05-05 3314
3314
