Модели бинарного выбора

Модели бинарного выбора используются, когда субъект совершает

выбор между двумя возможными альтернативами. Выбор основывается на

наборе некоторых входных факторов, характеризующих альтернативы и

субъект. Обозначим сделанный выбор переменной Y, которая принимает

значение 0, когда выбрана первая альтернатива, иначе значение 1.

Входные факторы могут выражать и качественные, и количественные

признаки. Задача состоит в установлении взаимосвязи между зависимой

переменной и одной или более независимыми переменными, в общем

случае принимающими все действительные значения. В том случае, когда

возможных альтернатив несколько, модель называется моделью

множественного выбора. В данной работе рассматривается модель

бинарного выбора, как первый этап в изучении моделей множественного

выбора. В качестве примера применения таких моделей можно привести

социологический опрос или маркетинговые исследования, где выбор

между альтернативами зависит от предпочтений выбирающего и

характеристик объекта исследования.

Пусть Yi обозначает значение переменной Y, i=1,…n, где n –

количество выбирающих, и Xi =(xi1,…,xik) обозначает значения факторов, характеризующих выбор и выбирающего.

Самой простой является модель

линейной вероятности 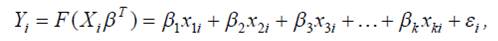[1]:

(1)

Где β — вектор коэффициентов регрессии, ε_i – независимо

распределенная случайная величина с нулевым математическим

ожиданием (в дальнейшем случайная ошибка).

Из предположения о нулевом математическом ожидании случайной

ошибки следует, что она принимает только дискретные значения [1, 2].

Поскольку Y i принимает только два значения, очевидно, что:

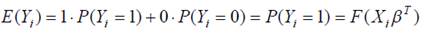
Таким образом, модель (1) может быть записана в виде

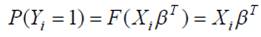
Для данной регрессионной зависимости возможно применение

метода наименьших квадратов, однако, результаты оценивания будут не

удовлетворительными с содержательной точки зрения. Недостатками

модели линейной вероятности является сложная интерпретация дробных

значений зависимых переменных, а также возможный выход за область

определения [0, 1] значений, как зависимых переменных, так и

прогнозных значений, которые по смыслу являются прогнозными

значениями вероятности выбора одной из альтернатив. В [1, 6]

представлена модель бинарного выбора, основанная на использовании

функции распределения F(•), область значений которой лежит в отрезке

[0, 1]:

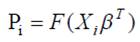(2)

Обычно используют два вида распределений:

1) функция логистического распределения

,

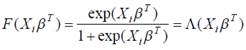соответствующую модель называют logit-моделью.

2) функция нормального распределения

,

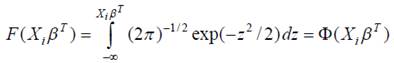соответствующую модель называют probit-моделью. Предполагается, что в основе выбора

альтернатив лежит некоторая ненаблюдаемая количественная переменная

Y*, связанная с входными переменными регрессионным уравнением:

,

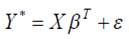где ошибки ε независимы и одинаково распределены с нулевым средним и

дисперсией σ. Наблюдается только дискретная величина Y, которая

связана с Y* следующим соотношением: Y=1, если Y*

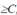; иначе Y=0.

Пороговое значение С, без ограничения общности принимаемое равным

нулю, если константа включена в число регрессоров. Примером

порогового значения С будет накопление семьи, которая принимает

решение о покупке холодильника. Предполагая, что случайные ошибки

имеют одно и тоже симметричное распределение F(•)=1–F(•), получаем

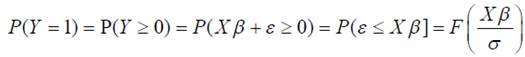, что с точностью до нормировки совпадает с (2). Параметры β и σ

участвуют только в виде отношения и не могут быть по отдельности

идентифицированы, поэтому в данном случае можно считать, что σ =1.

Другая интерпретация модели выбора [3, 5] предполагает, что

выбор осуществляется на основе ненаблюдаемой полезности альтернатив

U=U(Y,X). Если U(1,X)>U(0,X), то выбираем Y=1, иначе Y=0. В

простейшем случае полезность является линейной функцией регрессоров:

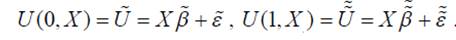
Эта модель сводится к пороговой, если взять

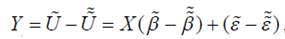, С = 0.

Таким образом, характер модели (2) можно интерпретировать как

выбор альтернативы, наиболее полезной для выбирающего. Случайная

ошибка, включенная в модель, учитывает два ключевых момента: 1) с одним и тем же набором факторов могут быть выбраны различные

альтернативы; 2) выбирающий может выбрать не максимально полезную

альтернативу, что демонстрирует иррациональное поведение.

Поскольку эти логистическое и нормальное распределения очень

близки, вопрос о том, какое из них использовать очень сложен.

В данной работе выбрана logit-модель в

силу простоты численной реализации процедуры оценивания параметров.