Теорема о трехмерной реализации графа

Любой конечный граф допускает геометрическую реализацию в трехмерном пространстве.

Доказательство. Пусть , ,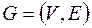

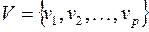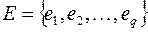. Проведем в трехмерном пространстве прямую, на которой отложим точки 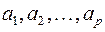, через эту прямую проведем 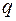полуплоскостей, и каждую кривую 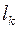, соответствующую ребру 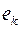, расположим в своей полуплоскости. Получим геометрическую реализацию графа.

Определение. Граф называется планарным (или плоским), если допускает геометрическую реализацию на плоскости.

Для геометрической реализации графа на плоскости можно ввести понятие грани. Гранью называют часть плоскости, ограниченную циклом. Грань может быть конечной и бесконечной.

На рис. 23 приведена геометрическая реализация плоского трехкомпонентного графа, имеющего 3 конечные грани: 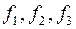и одну бесконечную грань .

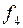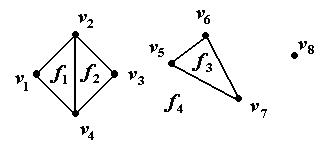Рис. 23

Формула Эйлера для связного планарного графа.

Пусть 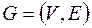– связный планарный граф, 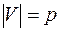, 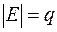. Тогда для любой геометрической реализации графа на плоскости справедлива формула

,

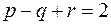где 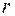– число граней.

Доказательство. Докажем теорему по индукции по 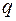при фиксированном .

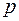а) База индукции. Минимальный связный граф – дерево, для него 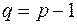(рис. 24). Так как дерево – граф без циклов, то у него всего одна бесконечная грань. Тогда 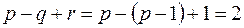, формула верна.

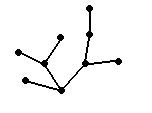Рис. 24

б) Пусть формула справедлива для графа с 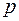вершинами и 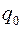ребрами, где .

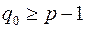в) Докажем, что она справедлива для графа с 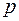вершинами, 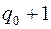ребрами и 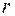гранями.

Рассмотрим геометрическую реализацию графа на плоскости. Так как 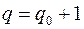, то 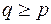, и граф не является деревом, тогда в графе существует цикл. Пусть ребро 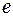входит в цикл, оно разделает 2 грани (рис. 25).

Рассмотрим граф 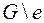, он связен, планарен, в нем 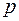вершин, 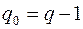ребер и 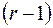грань, по индуктивному предположению, для него верна формула Эйлера 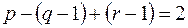или 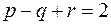, теорема доказана.

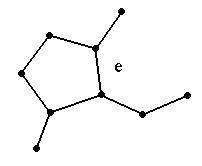Рис. 25

Формула Эйлера для несвязного планарного графа.

Пусть граф 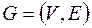имеет 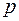вершин, 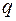ребер и связных компонент. Тогда для любой геометрической реализации его на плоскости справедлива формула

,

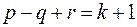где 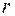– число граней.

Доказательство. 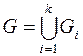, , 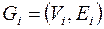пусть 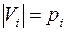, 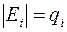и для 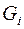справедлива формула Эйлера

.

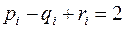Просуммируем обе части по . . 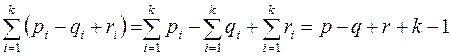, так как бесконечная грань в – связном графе должна учитываться только 1 раз, а в 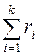мы учли ее раз, поэтому 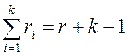. Отсюда 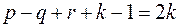или .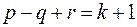

Следствие 1. Формула Эйлера справедлива для геометрической реализации графа на сфере.

Пусть 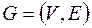– связный граф с 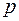вершинами и 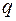ребрами. Каждой вершине графа поставлена в соответствие точка на сфере, различным вершинам 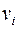и 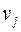– разные точк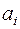и и 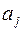. Каждому ребру 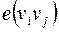поставлена в соответствие кривая 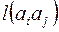, лежащая на сфере, и кривые не имеют общих точек, кроме, быть может, концевых – получена геометрическая реализация графа на сфере. Для нее справедлива формула

.

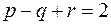Доказательство. Пусть точка 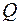принадлежит какой-либо грани. Возьмем ее в качестве полюса и стереографически спроектируем сферу на плоскость. Граф так же спроектируется на плоскость. Если кривые на сфере не пересекались, то их проекции на плоскость также не будут пересекаться – получим геометрическую реализацию графа на плоскости, число вершин, ребер и граней сохранится. (Только грань, содержащая точку 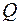, станет бесконечной гранью). Для геометрической реализации на плоскости формула Эйлера верна: .

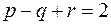Следствие 2. В любом выпуклом многограннике .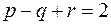

Доказательство. Поместим многогранник в сферу и рассмотрим центральную проекцию многогранника на сферу. Получим геометрическую реализацию графа с 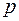вершинами, 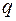ребрами и 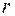гранями на сфере, для которой формула доказана.