1 -вариант
Задача 1.
Выполнить округление приближенных чисел и записать результат с учетом верных цифр:
a = - 0.5689176,  a = 0.005
a = 0.005
b = 1.386222 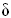 b = 0.02
b = 0.02
Задача 2.
Высота и радиус основания цилиндра измерены с точностью до 0.5%. Какова относительная погрешность при вычислении объема цилиндра?
2 -вариант
Задача 1.
Выполнить округление приближенных чисел и записать результат с учетом верных цифр:
a = - 13.3526869,  a = 0.005
a = 0.005
b = 0. 623827 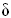 b = 0.02
b = 0.02
Задача 2.
Высота и радиус основания конуса измерены с точностью до 0.3%.
Какова относительная погрешность при вычислении объема конуса?
 |
| 2.1. Понятие значащих цифр |
Определение 2.1. Все цифры десятичной записи числа, начиная с первой ненулевой слева, называются значащими цифрами этого числа. Нули в конце числа всегда считаются значащими, в противном случае их не пишут. Так, число 0,05020 содержит четыре значащие цифры: 5, 0, 2 и 0. Абсолютную погрешность не следует записывать с большим количеством значащих цифр. Основной информацией, содержащейся в ней, являются значение первой ненулевой цифры и десятичный разряд, в котором эта цифра расположена. Правило. В записи абсолютной погрешности обычно оставляют только одну или две значащие цифры. Для сохранения условия (1.1) округление при этом всегда производится с избытком. (Пример 2.1) Как и всякое действительное число, абсолютную погрешность можно записывать в так называемой плавающей форме (с плавающей десятичной запятой) 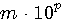 . Здесь m называется мантиссой числа, а р — его порядком. Например, . Здесь m называется мантиссой числа, а р — его порядком. Например, 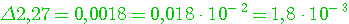 . С помощью абсолютных погрешностей определяют так называемые верные значащие цифры приближенных чисел. Пусть приближенное число записано в виде десятичной дроби: . С помощью абсолютных погрешностей определяют так называемые верные значащие цифры приближенных чисел. Пусть приближенное число записано в виде десятичной дроби: 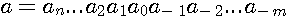 , т.e. , т.e. 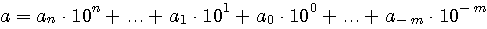 . . |
| 2.2. Верные значащие цифры в нестрогом (широком) смысле |
Определение 2.2. Значащая цифра приближенного значения а, находящаяся в разряде, в котором выполняется условие: абсолютная погрешность 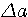 не превосходит половину единицы этого разряда, называется верной. Значащие цифры разрядов, где не выполняется данное условие, называются сомнительными. Следовательно, значащая цифра не превосходит половину единицы этого разряда, называется верной. Значащие цифры разрядов, где не выполняется данное условие, называются сомнительными. Следовательно, значащая цифра 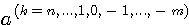 верная, если верная, если 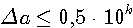 . Понятно, что все значащие цифры, расположенные слева от верной, также будут верными, а расположенные справа от сомнительной - сомнительными. Соответствующие десятичные разряды также называем верными или сомнительными. (Пример 2.2.) Для выявления верных цифр числа а без проверки каждой из них «по определению» рекомендуется следующее правило. Правило 1. Абсолютная погрешность округляется с избытком до одной значащей цифры (обозначим эту цифру буквой d). Если цифра . Понятно, что все значащие цифры, расположенные слева от верной, также будут верными, а расположенные справа от сомнительной - сомнительными. Соответствующие десятичные разряды также называем верными или сомнительными. (Пример 2.2.) Для выявления верных цифр числа а без проверки каждой из них «по определению» рекомендуется следующее правило. Правило 1. Абсолютная погрешность округляется с избытком до одной значащей цифры (обозначим эту цифру буквой d). Если цифра 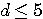 , то все значения цифры числа а левее того разряда, где находится d, будут верными. В противном случае последнюю (самую правую) из этих цифр следует признать сомнительной. (Пример 2.3) Верная цифра приблеженного числа не обязана буквально совпадать с цифрой соответствующего разряда точного числа. Например, пусть А =1,999 – точное число, а =2,000 – его приближение. Тогда , то все значения цифры числа а левее того разряда, где находится d, будут верными. В противном случае последнюю (самую правую) из этих цифр следует признать сомнительной. (Пример 2.3) Верная цифра приблеженного числа не обязана буквально совпадать с цифрой соответствующего разряда точного числа. Например, пусть А =1,999 – точное число, а =2,000 – его приближение. Тогда 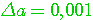 и, следовательно, три первых цифры числа а верные, хотя ни одна из них не совпадает с соответствующей цифрой числа А. Нередко бывает так, что исходные числовые данные приводятся без оценки их погрешности, но с известными верными цифрами. Возникает задача: найти абсолютные погрешности этих чисел, необходимые для последующего учета погрешностей. Решение следует из определения верной цифры. Если все три цифры числа а = 4,06 верные, это означает, что и, следовательно, три первых цифры числа а верные, хотя ни одна из них не совпадает с соответствующей цифрой числа А. Нередко бывает так, что исходные числовые данные приводятся без оценки их погрешности, но с известными верными цифрами. Возникает задача: найти абсолютные погрешности этих чисел, необходимые для последующего учета погрешностей. Решение следует из определения верной цифры. Если все три цифры числа а = 4,06 верные, это означает, что 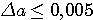 . Во избежание искусственного завышения степени точности числа мы не имеем права взять конкретное . Во избежание искусственного завышения степени точности числа мы не имеем права взять конкретное 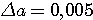 , например, , например, 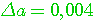 , поэтому принимаем , поэтому принимаем 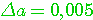 . Отсюда следует правило. Правило 2. За абсолютную погрешность приближенного числа с известными верными значащими цифрами принимается половина единицы того разряда, где находится последняя верная цифра. Обратим внимание на информационную значимость нулей, записанных в конце числа. Так, если известно, что все цифры чисел 3,2 и 3,20 верные, то эти записи не равноценны. За абсолютную погрешность первого числа можно взять 0,05, а второго – 0,005. В приближенных вычислениях часто используется другое определение верной значащей цифры. Определение 2.3. Если абсолютная погрешность числа не превосходит единицы того разряда, где находится значащая цифра, то эта цифра называетсяверной в нестрогом (широком) смысле. Таким образом, для верной в нестрогом смысле цифры . Отсюда следует правило. Правило 2. За абсолютную погрешность приближенного числа с известными верными значащими цифрами принимается половина единицы того разряда, где находится последняя верная цифра. Обратим внимание на информационную значимость нулей, записанных в конце числа. Так, если известно, что все цифры чисел 3,2 и 3,20 верные, то эти записи не равноценны. За абсолютную погрешность первого числа можно взять 0,05, а второго – 0,005. В приближенных вычислениях часто используется другое определение верной значащей цифры. Определение 2.3. Если абсолютная погрешность числа не превосходит единицы того разряда, где находится значащая цифра, то эта цифра называетсяверной в нестрогом (широком) смысле. Таким образом, для верной в нестрогом смысле цифры 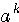 , должно выполнятся неравенство , должно выполнятся неравенство 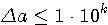 . . |
| 2.3. Верные значащие цифры в строгом (узком) смасле |
Для отличия цифру, верную в смысле определения 2.2. называют верной в строгом (узком) смысле. Нетрудно проверить: верная в строгом смысле цифра будет верной и в нестрогом смысле, а обратное утверждение не имеет места. Итак, значащими цифрами числа называют все цифры в его записи, начиная с первой с первой ненулевой слева. Значащую цифру называют верной, если абсолютная погрешность числа, не превосходит единицы разряда, соответствующего этой цифре. (Иногда уславливаются называть значащую цифру верной, если абсолютная погрешность не превосходит половины единицы разряда, соответствующих этой цифре.) Иногда употребляется термин число верных цифр после запятой: подсчитывается число цифр после запятой от первой цифры до последней верной цифры. Абсолютную или относительную погрешность обычно записывают в виде числа, содержащего одну или две значащих цифры. Информацию о том, что а* является приближенным значением числа а с абсолютной погрешностью 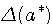 , иногда записывают в виде , иногда записывают в виде 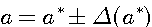 . Числа а* и . Числа а* и 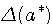 принято записывать с одинаковым числом знаков после запятой. Например, записи принято записывать с одинаковым числом знаков после запятой. Например, записи 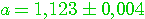 , , 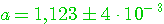 относятся к общепринятым и означают, что относятся к общепринятым и означают, что 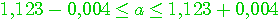 . Соответственно информация о том, что а* является приближенным значением числа а с относительной погрешностью . Соответственно информация о том, что а* является приближенным значением числа а с относительной погрешностью 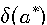 , записывают в виде: , записывают в виде: 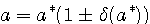 . Например, записи . Например, записи 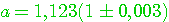 , , 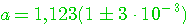 , , 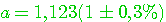 означает, что означает, что 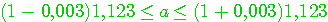 . . |
 |
| 1.Определение погрешности |
Пример 1.1. Пусть требуется оценить погрешность округления числа е = 2,7182818... до трех значащих цифр: e 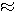 2,72. Для этого найдем расстояние от числа е до приближения 2,72: 2,72. Для этого найдем расстояние от числа е до приближения 2,72: 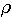 (е; 2,72) = | е - 2,72 | = 0,00171817.... Оно является иррациональным числом и потому неудобным для использования. Введем абсолютную погрешность (е; 2,72) = | е - 2,72 | = 0,00171817.... Оно является иррациональным числом и потому неудобным для использования. Введем абсолютную погрешность 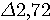 . При записи с двумя значащими цифрами с соблюдением условия (1.1) следует взять . При записи с двумя значащими цифрами с соблюдением условия (1.1) следует взять 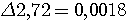 , но не 0,0017, как получилось бы при обычных правилах округления. Приемлемым значением , но не 0,0017, как получилось бы при обычных правилах округления. Приемлемым значением 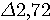 будет и 0,002 (с одной значащей цифрой). Пример 1.2. Для измерения длины l болта использованы метровая линейка с делениями 0,5 см и линейка с делениями 1 мм. В обоих случаях получен результат будет и 0,002 (с одной значащей цифрой). Пример 1.2. Для измерения длины l болта использованы метровая линейка с делениями 0,5 см и линейка с делениями 1 мм. В обоих случаях получен результат 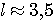 см. Ясно, что в первом случае отклонение найденной длины 3,5 см от истинной, не должно по модулю превышать 0,5 см, во втором случае 0,1 см. Если этот же результат получится при измерении штангенциркулем, то см. Ясно, что в первом случае отклонение найденной длины 3,5 см от истинной, не должно по модулю превышать 0,5 см, во втором случае 0,1 см. Если этот же результат получится при измерении штангенциркулем, то 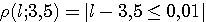 . Данный пример показывает зависимость абсолютной погрешности и границ, в которых находится точный результат, от точности измерительных приборов. В одном случае . Данный пример показывает зависимость абсолютной погрешности и границ, в которых находится точный результат, от точности измерительных приборов. В одном случае 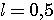 и, следовательно, и, следовательно, 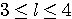 ; в другом - ; в другом - 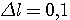 и и 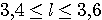 . Пример 1.3. На предприятии 1284 рабочих и служащих. При округлении до 1280 абсолютная погрешность составляет 1281280=4. Пример 1.4. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200-297=3. Относительная погрешность равна . Пример 1.3. На предприятии 1284 рабочих и служащих. При округлении до 1280 абсолютная погрешность составляет 1281280=4. Пример 1.4. В школе 197 учащихся. Округляем это число до 200. Абсолютная погрешность составляет 200-297=3. Относительная погрешность равна 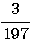 или, округленно или, округленно 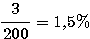 . Пример 1.5. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная относительная погрешность этого измерения? Здесь а=17,9; можно принять . Пример 1.5. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная относительная погрешность этого измерения? Здесь а=17,9; можно принять 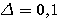 см,так как с точностью до 1 мм измерить карандаш не трудно, а значительно уменьшить предельную погрешность не удастся. Относительная погрешность равна см,так как с точностью до 1 мм измерить карандаш не трудно, а значительно уменьшить предельную погрешность не удастся. Относительная погрешность равна 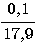 . Округляя, находим . Округляя, находим 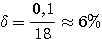 . . |
| 2.Значащие цифры |
Пример 2.1. Для приближенного числа x = 72,356 известна абсолютная погрешность 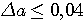 . Требуется определить его верные значащие цифры. Проверим цифру 7. Половина единицы ее разряда: . Требуется определить его верные значащие цифры. Проверим цифру 7. Половина единицы ее разряда: 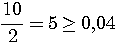 . Значит, она верная. Цифра 2: . Значит, она верная. Цифра 2: 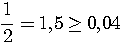 - тоже верная. Верной будет и цифра 3 (аналогично), а вот цифры 5 и 6 — сомнительные. Действительно, для 5: - тоже верная. Верной будет и цифра 3 (аналогично), а вот цифры 5 и 6 — сомнительные. Действительно, для 5: 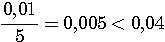 , т.е. требуемое условие нарушено. Результат, полученный в данном примере приводит к мысли о том, что цифры приближенного числа а верны во всех тех разрядах, где им соответствуют нули абсолютной погрешности. Однако это предположение верно лишь частично, ибо последняя такая цифра может оказаться сомнительной. Будет ли она верной, зависит от величины значащих цифр , т.е. требуемое условие нарушено. Результат, полученный в данном примере приводит к мысли о том, что цифры приближенного числа а верны во всех тех разрядах, где им соответствуют нули абсолютной погрешности. Однако это предположение верно лишь частично, ибо последняя такая цифра может оказаться сомнительной. Будет ли она верной, зависит от величины значащих цифр 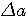 . Пример 2.2. Даны числа a, b, c и их абсолютные погрешности: а=2,645 b=0,81726 c=3968 . Пример 2.2. Даны числа a, b, c и их абсолютные погрешности: а=2,645 b=0,81726 c=3968 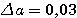 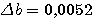 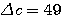 Видим, что цифры 2, 6, 4 числа а верные, так как соответствующая разряду тысячных долей цифра d = 3 абсолютной погрешности Видим, что цифры 2, 6, 4 числа а верные, так как соответствующая разряду тысячных долей цифра d = 3 абсолютной погрешности 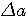 меньше 5. Число b имеет только одну верную значащую цифру 8. Действительно, при округлении с избытком его абсолютной погрешности получим число 0,006, содержащее в разряде тысячных долей значащую цифру d = 6 > 5, которая «портит» разряд сотых долей числа b. У целого числа с цифры верны в разрядах тысяч и сотен: это 3 и 9. Когда в конце числа получаются верные значащие нули округления, их следует сохранить. Пусть а = -17,30, но не меньше 5. Число b имеет только одну верную значащую цифру 8. Действительно, при округлении с избытком его абсолютной погрешности получим число 0,006, содержащее в разряде тысячных долей значащую цифру d = 6 > 5, которая «портит» разряд сотых долей числа b. У целого числа с цифры верны в разрядах тысяч и сотен: это 3 и 9. Когда в конце числа получаются верные значащие нули округления, их следует сохранить. Пусть а = -17,30, но не 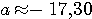 . Округление целого числа с из данного примера до верных цифр дает результат: . Округление целого числа с из данного примера до верных цифр дает результат: 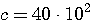 . . |
| 3.Правила округления |
| Пример 3.1. Округляя число 27,874 до трех значащих цифр, пишем 27,9. Третья цифра 8 усилена до 9, так как первая отбрасываемая цифра 7 больше, чем 5. Число 27,9 ближе к данному, чем неусиленное округленное число 27,8. Пример 3.2. Округляя число 36,251 до первого десятичного знака, пишем 36,3. Цифра десятых 2 усилена до 3, так как первая отбрасываемая цифра равна 5, а за ней есть значащая цифра 1. Чило 36,3 ближе к данному (хотя и незначительно), чем неусиленное число 36,2. Пример 3.3. Округляя число 27,48 до единиц, пишем 27. Это число ближе к данному, чем 28. Пример 3.4. Округляя число 0,0465 до третьего десятичного знака, пишем 0,046. Усиление не делаем, так как последняя сохраняемая цифра 6 - четная.Число 0,046 столь же близко к денном, как 0,047. |
| 4.Оценка погрешностей арифметических действий |
Пример 4.1. Пусть в выражении 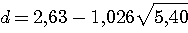 все числа приближенные и записаны с верными цифрами. Требуется найти значение d и определить абсолютную и относительную погрешности. Oбозначим: а = 5,40, все числа приближенные и записаны с верными цифрами. Требуется найти значение d и определить абсолютную и относительную погрешности. Oбозначим: а = 5,40, 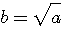 , , 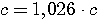 . Тогда . Тогда 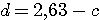 . Пока не известно, со сколькими значащими цифрами надо вычислить . Пока не известно, со сколькими значащими цифрами надо вычислить 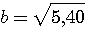 , так как абсолютная погрешность числа b неизвестна. Чтобы подсчитать , так как абсолютная погрешность числа b неизвестна. Чтобы подсчитать 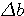 возьмем грубо возьмем грубо 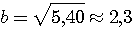 . Поскольку . Поскольку 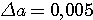 , на основании формул дифференциальной погрешности значения f(a) дифференцируемой функции y=f(x) в точке а: , на основании формул дифференциальной погрешности значения f(a) дифференцируемой функции y=f(x) в точке а: 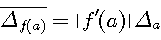 ; ; 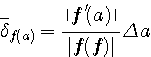 , , 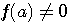 будем иметь будем иметь 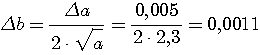 Следовательно, у числа b две цифры после десятичной запятой будут верными и его надо вычислить более точно: Следовательно, у числа b две цифры после десятичной запятой будут верными и его надо вычислить более точно: 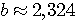 (с одной сомнительной цифрой). Относительная погрешность (с одной сомнительной цифрой). Относительная погрешность 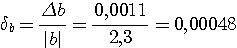 Оценим погрешность произведения Оценим погрешность произведения 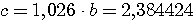 , взяв для этого , взяв для этого 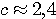 . Учитывая, что . Учитывая, что 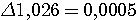 , подсчитаем сначала , подсчитаем сначала 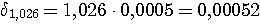 , а затем , а затем 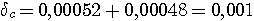 и и 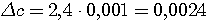 . Последний результат говорит о том, что в произведении три верные цифры и для дальнейших вычислений надо брать . Последний результат говорит о том, что в произведении три верные цифры и для дальнейших вычислений надо брать 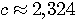 . Первое число в разности d = 2,63 – с имеет абсолютную погрешность 0,005, поэтому . Первое число в разности d = 2,63 – с имеет абсолютную погрешность 0,005, поэтому 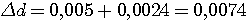 . В итоге получим результат . В итоге получим результат 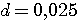 с одной верной значащей цифрой. Его относительная погрешность с одной верной значащей цифрой. Его относительная погрешность 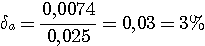 . Отметим, что результат в данном примере получен со значительно меньшей точностью по сравнению с точностью исходных данных, как по количеству верных значащих цифр, так и по значению относительной. Причиной этого явилось последнее действие, в котором разность двух чисел с тремя верными значащими цифрами оказалась только с одной такой цифрой. Пример 4.2. Складываютя приближенные числа 265 и 32. Пусть предельная пгрешность первого есть 5, а второго 1. Тогда предельная погрешность суммы равна 5+1=6. Так, если истенное значение первого есть 270, а второго 33, то приближенная сумма (265+32=297) на 6 меньше истенной (270+33=303). Пример 4.3. Пусть предельная погрешность приближенного уменьшаемого 85 равна 2, а предельная погрешность вычитаемого 32 равна 3. Предельная погрешность разности 85-32=53 есть 2+3=5. В самом деле, истенное значение уменьшаемого и вычитаемого могут равняться 85+2=87 и 32-3=29. Тогда истинная разностьесть 87-29=58. Она на 5 отличается от приближенной разности 53. Пример 4.4. Пусть перемножаютя приблеженные числа 50 и 20, и пусть предельная относительная погрешность первого сомножителя есть 0,4%, а второго 0,5%. Тогда предельная относительная погрешность произведения 50 . Отметим, что результат в данном примере получен со значительно меньшей точностью по сравнению с точностью исходных данных, как по количеству верных значащих цифр, так и по значению относительной. Причиной этого явилось последнее действие, в котором разность двух чисел с тремя верными значащими цифрами оказалась только с одной такой цифрой. Пример 4.2. Складываютя приближенные числа 265 и 32. Пусть предельная пгрешность первого есть 5, а второго 1. Тогда предельная погрешность суммы равна 5+1=6. Так, если истенное значение первого есть 270, а второго 33, то приближенная сумма (265+32=297) на 6 меньше истенной (270+33=303). Пример 4.3. Пусть предельная погрешность приближенного уменьшаемого 85 равна 2, а предельная погрешность вычитаемого 32 равна 3. Предельная погрешность разности 85-32=53 есть 2+3=5. В самом деле, истенное значение уменьшаемого и вычитаемого могут равняться 85+2=87 и 32-3=29. Тогда истинная разностьесть 87-29=58. Она на 5 отличается от приближенной разности 53. Пример 4.4. Пусть перемножаютя приблеженные числа 50 и 20, и пусть предельная относительная погрешность первого сомножителя есть 0,4%, а второго 0,5%. Тогда предельная относительная погрешность произведения 50  20=1000 приближенно равна 0,9%. В самом деле предельная абсолютная погрешность первого сомножителя есть 50 20=1000 приближенно равна 0,9%. В самом деле предельная абсолютная погрешность первого сомножителя есть 50  0,004=0,2, а второго 20 0,004=0,2, а второго 20  0,005=0,1. Поэтому истенная величина произаедения не больше, чем (50+0,2) 0,005=0,1. Поэтому истенная величина произаедения не больше, чем (50+0,2)  (20+0,1)=1009,02, и не меньше, чем (50-0,2) (20+0,1)=1009,02, и не меньше, чем (50-0,2)  (20-0,1)=991,022. Если истинная величина произведения есть 1009,02, то погрешность произведения равна 1009,2-1000=9,02, а если 991,02, то погрешность произведения равна 1000-991,02=8,98. Рассмотренные два случая - самые неблагоприятные. Значит, предельная абсолютная погрешность произведения есть 9,02. Предельная относительная пгорешность равна 9,02:1000=0,902%, т.е. приближенно 0,9%. (20-0,1)=991,022. Если истинная величина произведения есть 1009,02, то погрешность произведения равна 1009,2-1000=9,02, а если 991,02, то погрешность произведения равна 1000-991,02=8,98. Рассмотренные два случая - самые неблагоприятные. Значит, предельная абсолютная погрешность произведения есть 9,02. Предельная относительная пгорешность равна 9,02:1000=0,902%, т.е. приближенно 0,9%. |
 2015-05-10
2015-05-10 2999
2999