Типовые распределения

Биномиальный закон распределения.

Пусть производится n независимых испытаний, в каждом из которых событие А может появится либо не появится. Вероятность наступления события во всех испытаниях постоянна и равна p (следовательно, вероятность непоявления q = 1 - p).Рассмотрим в качестве дискретной случайной величины X число появлений события А в этих испытаниях.

Очевидно, событие А в n испытаниях может либо не появится, либо появится 1 раз, либо 2 раза, …, либо n раз.

Дискретная величина Х имеет биномиальный закон распределения с параметрами n и p, если она принимает значения 0,1,2,…,m,…, n с вероятностями

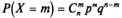, где 0<p<1, q = 1 – p.

Вероятности P(X=m) находятся по формуле Бернулли.

Т.о. биномиальный закон распределения представляет собой закон распределения числа X=m наступлений события А в n независимых испытаниях, в каждом из которых оно может произойти с одной и той же вероятностью p.

Ряд распределения биномиального закона имеет вид:

Сумма всех вероятностей представляет собой сумму всех членов разложения бинома Ньютона (отсюда и название закона - биномиальный):

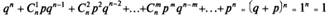
Математическое ожидание случайной величины Х, распределенной по биномиальному закону, M(X) = np, а ее дисперсия D(X) = npq.

Пуассоновское распределение.

Поставим задачу найти вероятность того, что при очень большом числе испытаний n, в каждом из которых вероятность p события A очень мала, событие наступит ровно k раз. Сделаем важное допущение: произведение np сохраняет постоянное значение, а именно np=λ. Это означает, что среднее число появлений события в различных сериях испытаний, т.е. при различных значениях n, остается неизменным.

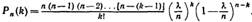
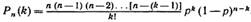Воспользуемся формулой Бернулли для вычисления интересующей нас вероятности: Так как p=λ/n, то

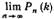Приняв во внимание, что n имеет очень большое значение, вместо P_n(k) найдем При этом будет найдено лишь приближенное значение отыскиваемой величины: n хотя и велико, но конечно, а при отыскании предела мы устремим n к бесконечности. Заметим, что поскольку произведение np сохраняет постоянное значение, то при n→∞ вероятность p→0.

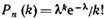Для простоты знак приближенного равенства опущен

Ряд распределения Пуассона имеет вид

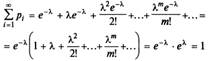
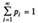Определение закона Пуассона корректно, так как основное свойство ряда распределения выполнено, поскольку сумма ряда (учтено, что в скобках записано разложение в ряд функции е­^х при х = λ).

Математическое ожидание и дисперсия случайной величины, распределенной по закону Пуассона, совпадают и равны параметру λ этого закона, т.е. М(Х)=λ, D(X)=λ.

При p→0, n→∞, np→λ=const закон распределения Пуассона является предельным случаем биномиального закона.

Так как при этом вероятность p события А в каждом испытании мала, то закон распределения Пуассона называют часто законом редких явлений.

Если случайная величина представляет собой сумму двух независимых случайных величин, распределены каждая по закону Пуассона, то она также распределена по закону Пуассона.