Вычисление рекуррентных последовательностей

Существуют задачи, в которых количество повторений циклов (итераций) заранее неизвестно, поскольку момент окончания цикла определяется заданной точностью вычислений, которая сама может изменяться по желанию пользователя. Рассмотрим решение подобных задач на примере обработки ряда числовой последовательности, когда работа цикла строится на использовании рекуррентных формул.

Пример. Вычислить сумму членов ряда последовательности .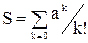

Пусть 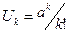- это k-й член ряда. Вычисление суммы S продолжается, пока |U_k|>eps, где eps – заданная точность вычислений, например .

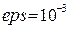Для вычисления суммы членов ряда, необходимо вывести рекуррентные формулы для члена ряда и для суммы ряда, которые позволяют вычислять текущие значения величины как функцию от предыдущих значений, например, .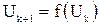

Вывод рекуррентной формулы члена ряда:

;

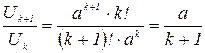отсюда .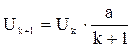

Для рекуррентных формул необходимо задавать начальное значение для неизвестной величины в правой части формулы (U_k): если k= 0, то

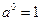, 0! = 1 и значит U₀= 1.

Рекуррентная формула суммы ряда:

,

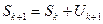где начальное значение S₀=U₀=1.

При составлении алгоритма и программы нижние индексы величин U, S опускаются, а сами эти величины используются как обозначения переменных.

Программа:

# include<math.h> /* для вычисления модуля (U) */

void main()

{ int k=0; float a, U, eps; double S; /* описание переменных */

clrscr (); /* очистка экрана */

printf (“Введите значения a, eps: ”);

scanf (“%f%f ”, &a, &eps); /* ввод чисел */

S=U=1; /* начальные значения */

while (fabs (u)>eps) /* условие продолжения цикла */

{ U +=a / (k+1); /* новый член ряда * /

S += U; /* новая сумма ряда */

k++; /* новый номер члена ряда */

}

printf (“Сумма S = %lf “, S); /* вывод результата */

}