Пересечение поверхности вращения с плоскостью общего положения

Для определения сечения поверхности вращения плоскостью общего положения использован способ замены плоскостей проекций, таким образом плоскость Д АВС на П₄ стала проецирующей. После определения сечения показываем видимость.

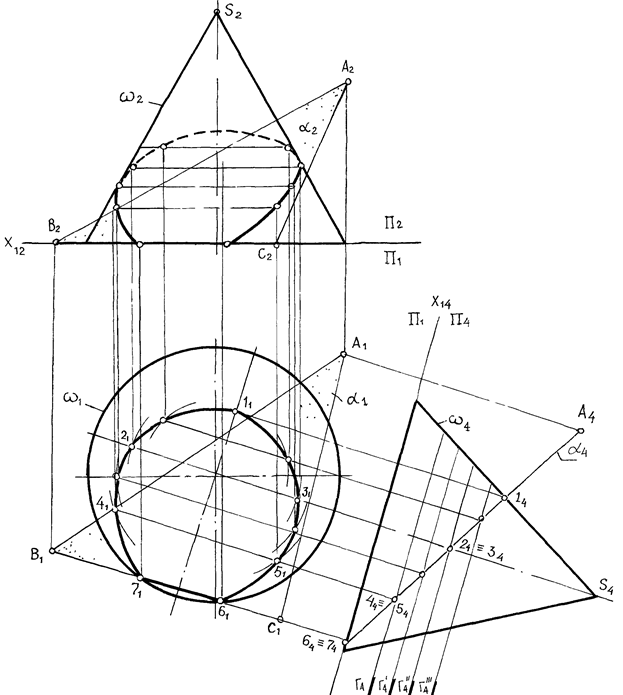
Рис. 53. Построение проекций эллипса в коническом сечении способом замены плоскостей проекций

Тор

Лат. torus – вздутие, выпуклость. Поверхность образована вращением окружности вокруг компланарной с ней прямой – оси тора. Различают:
о т к р ы т ы й т о р (тор-кольцо), его эксцентриситет е = r/R < 1 (рис. 55); с а-
м о с о п р и к а с а ю щ и й с я т о р (закрытый тор), е = r/R > 1 (рис. 56, б). Закрытый тор можно также рассматривать как множество точек пространства, из которых данный отрезок виден под углами a и b при условии, что
a + b = 180 (рис. 57, а). При a = b тор имеет сферу.

На рис. 56 обозначены проекции экватора m, горловины n и полярных (предельных, двойных) параллелей k и l открытого тора. Производная окружность и параллели образуют на торе ортогональную сеть. Точки на торе строят с помощью параллелей. На рис. показано построение проекций заданных точек A (A₂) и В (B₁).

Внутреннюю часть открытого тора (все точки которой, за исключением граничных полярных параллелей, имеют отрицательную кривизну) в технике называют глобоидом (похожа на глобус), рис. 59, а. Применяется в глобоидной червячной передаче (рис. 59, б). Особенно широко отсеки тора используют для образования плавных переходов между соосными поверхностями вращения

На рис. 54, а показано использование внутренней части соприкасающегося тора (тора-бочки). Некоторые сорта яблок имеют поверхность, довольно близкую к тору. Тор – алгебраическая поверхность 4-го порядка, выражаемая уравнением

(x² + y² + z² + R² – r²)² = 4RY(x² + y²).

Отсутствие в последнем множителя переменной говорит о том, что ось z – ось вращения (ось тора). Если ось вращения – ось х или y, множитель примет вид (y² + z²) или (x² + z²). Прямая может пересекать тор не более чем в четырех точках. Любое плоское сечение – кривая 4-го порядка. В частных случаях она может распадаться на две кривые 2-го порядка.

Кривые, получаемые при сечении тора плоскостями, параллельными его оси, в общем случае называют кривыми Персея, греческого геометра, жившего в IV в. до н. э. Заменив в уравнении тора соответствующую переменную величиной h (рис. 54), получим уравнение кривых в общем виде. В зависимости от соотношения между r, R, h частными видами кривых Персея могут быть: овалы Кассини (h = r), лемниската Бернулли (R = 2r; h = r)
(рис. 54), гиперболическая (R > r; h = R – r) или эллиптическая (R < r;
h = r – R) лемниската Бута, падеры гиперболы и эллипса относительно их центров соответственно. Кривые, получаемые при сечении тора плоскостями, наклонными к его оси (рис. 54, б), называют с п и р и ч е с к и м и (от греч. спайра-витой). В частном случае, когда плоскость касается тора в двух точках (точка А и В на рис. 58), спирическая линия распадается на два круга Вилларсо, называемых именем французского геометра, открывшего их в 1847 г. Очевидно, их горизонтальные проекции (z П₁) – эллипсы. На рис. 56 показано, как изменяется очертание тора в зависимости от наклона его оси к плоскости П₁. Строят очертания с помощью вспомогательных сфер, вписанных в тор. Аналогичный прием используют при построении аксонометрии тора (рис. 55), где кривая b' – эллипс, a' и с' – ветви его эквидистанты.

Top – классическая поверхность, содержащая точки всех трех видов (рис. 55). По мнению французских фантастов, будущие межпланетные станции будут иметь форму огромного тора. Поверхности, образуемые вращением какой-либо кривой, отличной от окружности, вокруг компланарной с ней прямой (но не являющейся осью), называют тороидальными (похожими на тор).

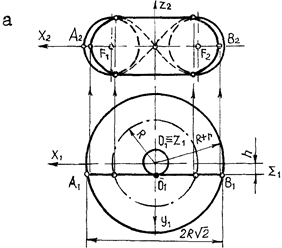
Рис. 54. Кривые Персея: а – лемниската Бернулли, б – спирическая
лемниската Бута