2015-05-13
8366
Задача о назначениях является типичным примером оптимального принятия управленческих решений. Эта задача позволяет распределить объекты из некоторого множества по группе субъектов из другого множества и это распределение должно соответствовать оптимальности одного или нескольких итоговых показателей.
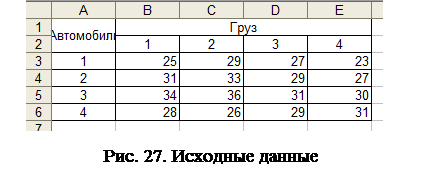
Постановка задачи. Пусть на предприятии имеется 4 разных грузовых автомобиля. Необходимо доставить разный товар в 4 разных района области. Общие затраты на перевозку каждого вида товара каждым автомобилем известны. Требуется так выбрать для каждого вида товара автомобиль так, чтобы суммарные затраты на перевозку были минимальными.
Исходные данные представлены на рис. 27.
 |
Математическая модель задачи о назначениях имеет следующий вид.
1. Переменные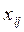 
принимают два значения:
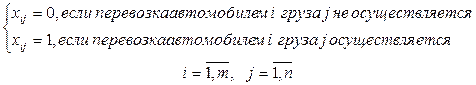(17)
2. Все переменные задачи – неотрицательные значения и целые числа:
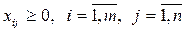(18)
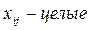
Также, так как каждый автомобиль может выполнять доставку только одного груза и весь груз должен быть доставлен, переменные должны отвечать следующим ограничениям:
|
|
|
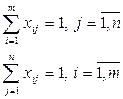(19)
Это условие означает, что выбор вариантов доставки должен быть таким, чтобы в таблице, представляющей решение задачи, было по одной единице в каждой строке и в каждом столбце. Остальные элементы должны равняться нулю.
3. Целевая функция, направленная на минимум суммарных затрат:
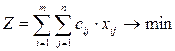(19)
Таким образом, алгоритм решения задачи о назначениях такой же, как у классической транспортной задачи (практическая работа №2).
Рассмотрим решение данной задачи.
На рис. 28 показано поле для решения задачи о назначениях.
 |
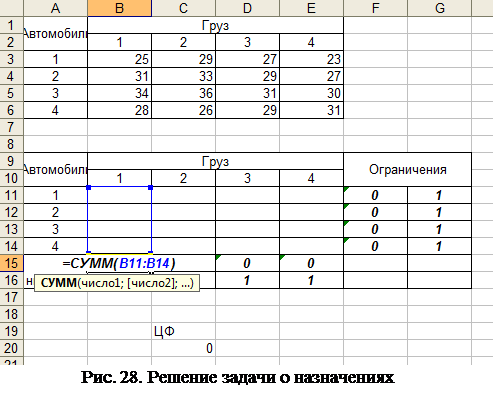В ячейки В15, С15, D15, Е15 заносится сумма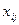 
по каждому соответствующему столбцу. В строки F11, F12, F13, F14 – сумма 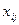по каждой строке. Каждая из сумм приравнивается к единице (то есть - может быть выбрана только одна ячейка в строке и в столбце).
Целевая функция рассчитывается как сумма произведений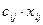 
:
 |
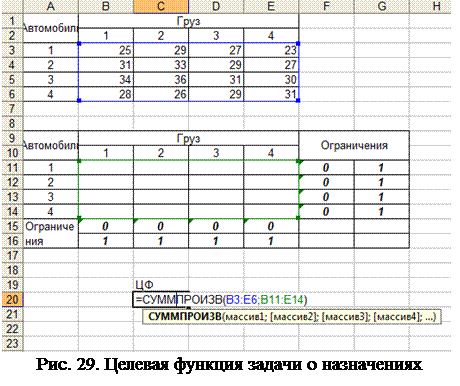«Поиск решения» производится следующим образом (рис. 30)
 |
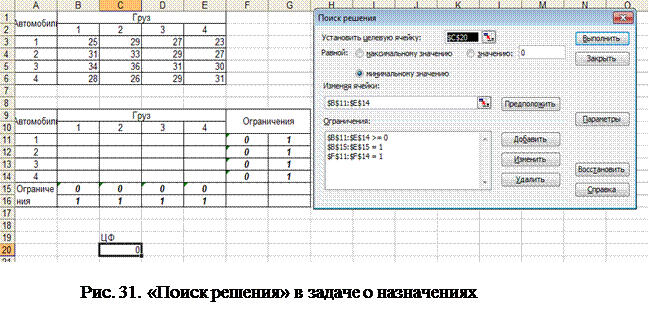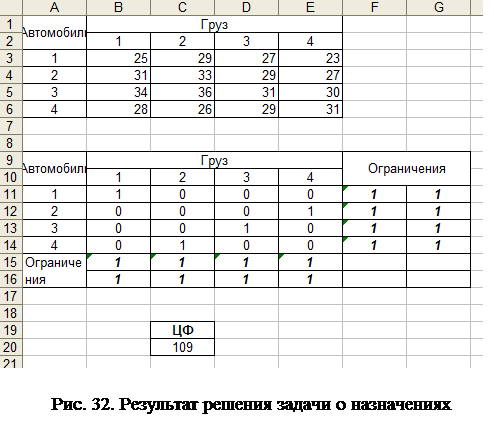
В меню «Параметры» «Поиска решения» необходимо установить «Линейная модель». Результаты расчетов приведены на рис. 32.
 |
