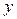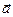При решении задач по динамике материальной точки необходимо прежде всего выяснить, какие силы действуют на тела рассматриваемой механической системы и изобразить их на рисунке. Затем нужно выбрать систему отсчета, относительно которой рассматривается движение. Координатные оси системы целесообразно располагать так, чтобы проекции сил на эти оси определялись наиболее просто. Для каждого тела системы необходимо записать второй закон Ньютона в векторной форме и спроектировать его на оси выбранной системы координат. Иногда оказывается, что полученных динамических уравнений недостаточно для решения задачи (в случае движения системы тел). Тогда необходимо дополнить систему уравнений кинематическими условиями, обусловленными связями, существующими между телами. Рассмотрим конкретные примеры.
Задача 1. Частица массы 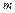 со скоростью
со скоростью 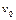 влетает в область действия тормозящей силы
влетает в область действия тормозящей силы 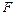 под углом
под углом 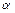 к направлению этой силы и вылетает под углом
к направлению этой силы и вылетает под углом 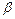 . Определить ширину
. Определить ширину 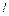 области действия тормозящей силы. Какой должна быть ширина области
области действия тормозящей силы. Какой должна быть ширина области 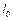 , чтобы частица могла из нее вылететь?
, чтобы частица могла из нее вылететь?
|
|
|
Решение
Будем рассматривать движение частицы в проекциях на направление действия тормозящей силы и перпендикулярное к нему (рис.1.2.1).
В первом случае движение будет равнозамедленным, и его кинематические уравнения можно записать в виде
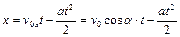 ,
,
(1.2.1)
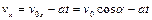 .
.
|
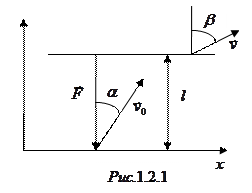 |
Движение в перпендикулярном к вектору силы направлении будет равномерным с постоянной скоростью
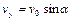 , и его уравнение примет вид
, и его уравнение примет вид
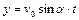 .
.
По условию через некоторое время вектор скорости образует с вектором силы угол 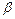 , откуда следует
, откуда следует
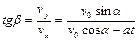 . (1.2.2)
. (1.2.2)
Из (1.2.2) находим время движения частицы в области действия тормозящей силы
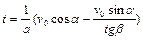 .
.
Согласно второму закону Ньютона 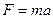 , следовательно,
, следовательно,
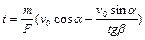 . (1.2.3)
. (1.2.3)
Подставляя (1.2.3) в (1.2.1), после несложных преобразований находим ширину области действия тормозящей силы
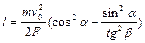 . (1.2.4)
. (1.2.4)
Предельно возможная ширина области действия силы может быть получена из (1.2.4), если положить 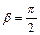 (в этот момент скорость частицы в направлении действия силы обращается в ноль). В результате получаем
(в этот момент скорость частицы в направлении действия силы обращается в ноль). В результате получаем
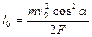 .
.
Задача 2. Каковы должны быть модуль и направление минимальной силы 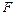 , приложенной к бруску, лежащему на горизонтальном столе, чтобы сдвинуть его с места? Масса бруска
, приложенной к бруску, лежащему на горизонтальном столе, чтобы сдвинуть его с места? Масса бруска 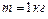 , коэффициент трения между столом и бруском
, коэффициент трения между столом и бруском 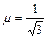 .
.
Решение
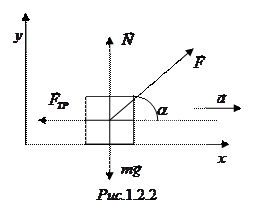
Силы, действующие на брусок, изображены на рис.1.2.2. Запишем второй закон Ньютона в проекциях на горизонтальное и вертикальное направления
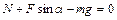 ,
, 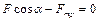 . (1.2.5)
. (1.2.5)
Максимальная сила трения покоя, как известно, пропорциональна силе нормальной реакции
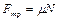 . (1.2.6)
. (1.2.6)
Решая систему уравнений (1.2.5), (1.2.6), находим
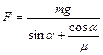 .
.
Полученное выражение можно рассматривать как функцию 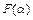 . Очевидно,
. Очевидно, 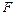 принимает наименьшее значение, когда знаменатель дроби становится максимальным. Так как производная знаменателя
принимает наименьшее значение, когда знаменатель дроби становится максимальным. Так как производная знаменателя 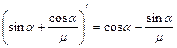 обращается в ноль при
обращается в ноль при 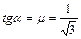 , сила
, сила 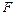 достигает наименьшего значения при
достигает наименьшего значения при 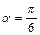 , когда
, когда
|
|
|
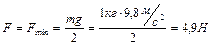 .
.
Задача 3. Определить силу, действующую на вертикальную стенку со стороны клина, если на него положили груз массой 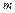 . Угол при основании клина
. Угол при основании клина 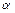 . Коэффициент трения между грузом и поверхностью клина
. Коэффициент трения между грузом и поверхностью клина 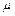 . Трения между клином и полом нет.
. Трения между клином и полом нет.
 |
Решение
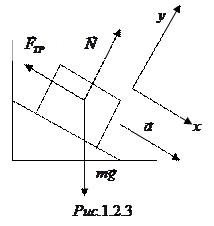
Силы, действующие на груз, показаны на рис.1.2.3. Уравнения движения груза (второй закон Ньютона) в проекциях на оси 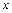 и
и 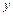 имеют вид
имеют вид
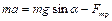 ,
, 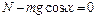 . (1.2.7)
. (1.2.7)
Сила трения скольжения
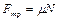 . (1.2.8)
. (1.2.8)
Из системы (1.2.7), (1.2.8) следует
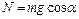 ,
, 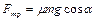 . (1.2.9)
. (1.2.9)
Согласно третьему закону Ньютона на клин со стороны груза должны действовать сила трения и сила нормального давления, направленные противоположно 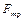 и
и 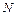 соответственно. Проектируя эти силы на горизонтальное направление, определим результирующую силу давления со стороны клина на стенку
соответственно. Проектируя эти силы на горизонтальное направление, определим результирующую силу давления со стороны клина на стенку
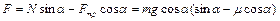 .
.
Полученный ответ будет являться правильным, если 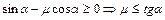 . В противном случае результирующая сил давления и трения будет направлена не к стенке, а от нее, следовательно,
. В противном случае результирующая сил давления и трения будет направлена не к стенке, а от нее, следовательно, 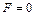 при
при 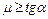 .
.
|
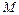 . Одновременно на каждый из грузов кладут по перегрузку: справа – массой
. Одновременно на каждый из грузов кладут по перегрузку: справа – массой 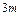 , слева – массой
, слева – массой 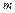 . Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.
. Определить ускорение системы, силу натяжения нити и силу давления перегрузков на основные грузы.
 |
Решение
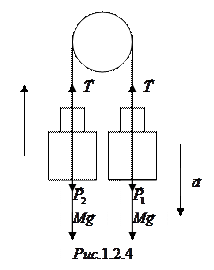
На рис.1.2.4 изображены силы, действующие на основные грузы. Проектируя уравнения движения грузов (второй закон Ньютона) на вертикальное направление, получаем
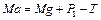 ,
, 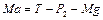 , (1.2.10)
, (1.2.10)
где 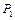 и
и 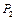 - силы давления перегрузков на основные грузы,
- силы давления перегрузков на основные грузы, 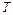 - сила натяжения нити.
- сила натяжения нити.
Рассматривая аналогично силы, действующие на перегрузки, получаем уравнения их движения:
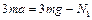 ,
, 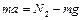 , (1.2.11)
, (1.2.11)
где  и
и 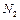 - силы реакции, действующие на перегрузки со стороны основных грузов.
- силы реакции, действующие на перегрузки со стороны основных грузов.
В силу третьего закона Ньютона
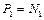 ,
, 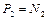 . (1.2.12)
. (1.2.12)
Решая систему уравнений (1.2.10) – (1.2.12) относительно ускорения, получаем
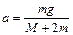 .
.
Используя полученный результат, находим силу натяжения нити
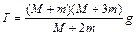 ,
,
и силы давления перегрузков на основные грузы
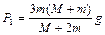 ,
, 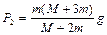 .
.
Задача 5. Два соприкасающихся бруска скользят по наклонной плоскости. Масса первого бруска 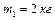 , второго
, второго 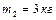 . Коэффициент трения между плоскостью и первым бруском
. Коэффициент трения между плоскостью и первым бруском 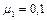 , между плоскостью и вторым бруском
, между плоскостью и вторым бруском 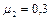 . Угол при основании наклонной плоскости
. Угол при основании наклонной плоскости 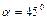 . Определить ускорение, с которым движутся бруски, и силу, с которой бруски давят друг на друга.
. Определить ускорение, с которым движутся бруски, и силу, с которой бруски давят друг на друга.
Решение
 |
Очевидно, что в силу соотношения
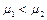 верхний брусок соскальзывал бы с большим ускорением, чем нижний, если бы они двигались отдельно друг от друга. Вследствие этого, верхний брусок будет давить на нижний, и они будут двигаться как одно целое.
верхний брусок соскальзывал бы с большим ускорением, чем нижний, если бы они двигались отдельно друг от друга. Вследствие этого, верхний брусок будет давить на нижний, и они будут двигаться как одно целое.
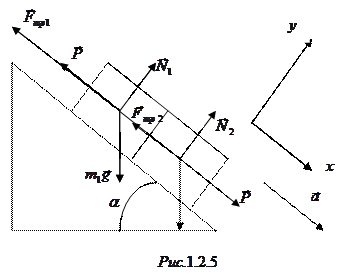
Изобразим на рис.1.2.5 силы, действующие на каждый брусок, и запишем уравнения их движения в проекциях на оси 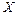 и
и 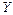 :
:
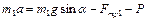 ,
, 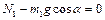 , (1.2.13)
, (1.2.13) 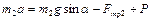 ,
, 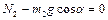 . (1.2.14)
. (1.2.14)
Дополним эту систему условиями пропорциональности сил трения и сил нормальной реакции
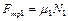 ,
, 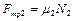 . (1.2.15)
. (1.2.15)
Решая систему (1.2.13) – (1.2.15), находим ускорение системы
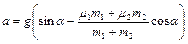 .
.
Используя полученный результат, находим силу взаимодействия грузов при их движении вдоль плоскости
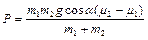 .
.
Задача 6. Какую горизонтальную силу 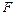 нужно приложить к тележке массой
нужно приложить к тележке массой 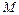 , чтобы бруски массой
, чтобы бруски массой 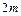 и
и 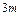 относительно нее не двигались? Трением пренебречь.
относительно нее не двигались? Трением пренебречь.
Решение
Силы, действующие на тележку и грузы, изображены на рис.1.2.6. Запишем второй закон Ньютона для этих тел, проектируя его на горизонтальное и вертикальное направления:
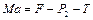 ,
, 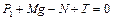 , (1.2.16)
, (1.2.16)
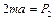 ,
, 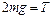 , (1.2.17)
, (1.2.17)
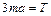 ,
, 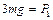 . (1.2.18)
. (1.2.18)
Здесь 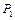 и
и 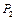 - силы давления брусков на тележку,
- силы давления брусков на тележку, 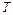 - сила натяжения нити,
- сила натяжения нити, 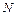 - сила реакции, действующая на тележку со стороны поверхности.
- сила реакции, действующая на тележку со стороны поверхности.
Появле 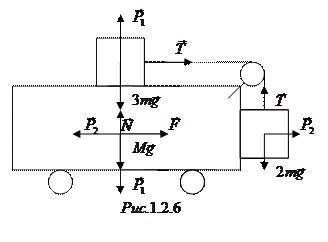
ние в (1.2.16) силы натяжения нити объясняется тем, что посредством нити бруски оказывают давление на ось блока, следовательно, в уравнении движения тележки необходимо учесть результирующую горизонтальной и вертикальной сил натяжения, направив ее противоположно тому, как это показано на рисунке.
|
|
|
Исключая из системы (1.2.16) – (1.2.18) ускорение, силы натяжения нити и давления брусков, находим
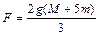 .
.
Задача 7. В вагоне поезда, идущего равномерно со скоростью 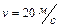 по закруглению радиусом
по закруглению радиусом 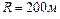 , производится взвешивание груза с помощью динамометра. Масса груза
, производится взвешивание груза с помощью динамометра. Масса груза 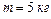 . Определить результат взвешивания.
. Определить результат взвешивания.
Решение
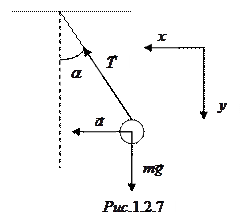 |
Силы, действующие на груз, показаны на рис.1.2.7. Применяя второй закон Ньютона в проекциях на оси
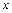 и
и 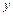 , получаем систему уравнений
, получаем систему уравнений
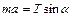 ,
, 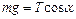 . (1.2.19)
. (1.2.19)
Здесь 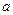 - центростремительное ускорение, равное по определению
- центростремительное ускорение, равное по определению
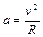 .
.
Возводя оба уравнения (1.2.19) в квадрат, складывая их и применяя основное тригонометрическое тождество, получаем
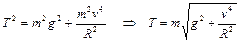 .
.
Согласно третьему закону Ньютона сила натяжения, действующая на груз, равна весу груза, а значит совпадает с показаниями динамометра. Подставляя числовые значения, находим ответ
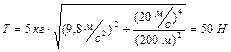 .
.
Задача 8. Шарик на нити, вращающийся равномерно в вертикальной плоскости, находится в лифте, движущемся с ускорением 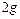 . Когда шарик находится в нижней точке своей траектории, натяжение нити равно нулю. Определить натяжение нити
. Когда шарик находится в нижней точке своей траектории, натяжение нити равно нулю. Определить натяжение нити 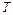 в момент, когда шарик находится в верхней точке своей траектории. Масса шарика
в момент, когда шарик находится в верхней точке своей траектории. Масса шарика 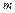 .
.
Решение

Перейдем в неинерциальную систему отсчета, движущуюся вмести с лифтом. Помимо обычных сил в такой системе отсчета на любое тело действует сила инерции, равная произведению массы тела на ускорение системы отсчета и направленная противоположно этому ускорению.
Определим предварительно направление ускорения лифта. Так как в нижней точке траектории натяжение нити исчезает, а ускорение шарика направлено к центру окружности, следовательно, на шарик должна действовать дополнительная сила инерции, направленная вертикально вверх. В результате приходим к выводу, что лифт движется вниз.
С учетом сказанного выше уравнение второго закона Ньютона для нижней точки траектории шарика в проекции на вертикальное направление примет вид
|
|
|
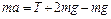 .
.
Согласно условию
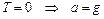 . (1.2.20)
. (1.2.20)
Тогда записывая уравнение второго закона Ньютона для верхней точки траектории, получаем
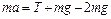 ,
,
что с учетом (1.2.20) приводит к ответу
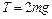 .
.
 2015-05-13
2015-05-13 7140
7140