При решении задач на свободные или вынужденные колебания, как правило, не требуется решать уравнения соответствующих колебаний. Достаточно определить значение силы, вынуждающей движение тела к положению равновесия и тогда, из сопоставления полученного уравнения и соответствующего уравнения колебаний можно определить период и частоту колебаний, а значит и найти закон движения тела. Рассмотрим конкретные примеры.
Задача 1. Математический маятник подвешен вблизи вертикальной стены и колеблется в плоскости, параллельной стене. В стену вбит гвоздь так, что середина нити маятника наталкивается на него каждый раз, когда маятник проходит положение равновесия справа налево. Найти длину нити, если период колебаний такого маятника (с помехой в виде гвоздя) 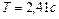 .
.
Решение
Очевидно, что период колебаний такого маятника равен полусумме периодов колебаний маятника с длиной нити 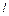 и маятника с длиной нити
и маятника с длиной нити 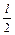 .
.
Используя известное выражение для периода колебаний математического маятника, получаем
|
|
|
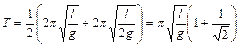 . (1.6.1)
. (1.6.1)
Выражая из (1.6.1) длину нити, находим
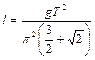 .
.
Подстановка числовых значений дает
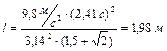 .
.
Задача 2. Груз массой 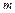 сбрасывается с высоты
сбрасывается с высоты 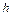 на чашку пружинных весов. Жесткость пружины
на чашку пружинных весов. Жесткость пружины 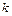 , масса чашки
, масса чашки 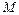 . Определить амплитуду колебаний. При какой высоте произойдет отрыв груза от чашки в верхней точке? Считать, что удар груза о чашку неупругий, но груз не прилипает к чашке.
. Определить амплитуду колебаний. При какой высоте произойдет отрыв груза от чашки в верхней точке? Считать, что удар груза о чашку неупругий, но груз не прилипает к чашке.
Решение
Воспользуемся законом сохранения энергии и определим скорость 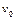 груза в момент удара о чашку
груза в момент удара о чашку
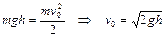 . (1.6.2)
. (1.6.2)
Для определения скорости 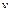 чашки вместе с грузом сразу после удара применяем закон сохранения импульса
чашки вместе с грузом сразу после удара применяем закон сохранения импульса
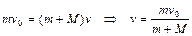 . (1.6.3)
. (1.6.3)
Пусть удлинение пружины перед падением груза равно 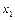 , а в момент максимального растяжения пружины после падения груза -
, а в момент максимального растяжения пружины после падения груза - 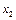 . Тогда применяя для движения чашки с грузом закон сохранения энергии, получаем
. Тогда применяя для движения чашки с грузом закон сохранения энергии, получаем
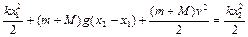 . (1.6.4)
. (1.6.4)
Так как из условия равновесия пружины под весом чашки 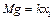 следует
следует 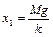 , то используя (1.6.2), (1.6.3), получаем квадратное уравнение относительно
, то используя (1.6.2), (1.6.3), получаем квадратное уравнение относительно 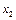 :
:
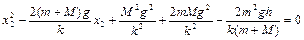 . (1.6.5)
. (1.6.5)
Решая (1.6.5), находим
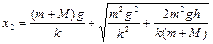 .
.
Определим равновесное удлинение 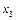 пружины под действием чашки вместе с грузом
пружины под действием чашки вместе с грузом
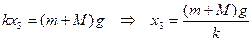 .
.
Поскольку амплитуда колебаний есть максимальное смещение тела от положения равновесия, получаем
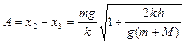 . (1.6.6)
. (1.6.6)
Условие отрыва груза от чашки в верхней точке состоит в исчезновении силы реакции со стороны чашки. По второму закону Ньютона это дает 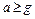 , где
, где 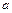 - ускорение груза. Поскольку
- ускорение груза. Поскольку 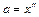 , а уравнение колебаний имеет вид
, а уравнение колебаний имеет вид 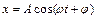 , максимальное значение ускорения
, максимальное значение ускорения 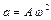 . Частота колебаний пружинного маятника определяется по формуле
. Частота колебаний пружинного маятника определяется по формуле 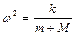 , следовательно, условие отрыва груза принимает вид
, следовательно, условие отрыва груза принимает вид
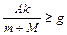 . (1.6.7)
. (1.6.7)
Подставляя (1.6.6) в (1.6.7) и решая относительно высоты падения, получаем
|
|
|
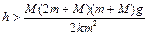 .
.
Задача 3. К колесу радиуса 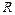 с горизонтально расположенной осью прикрепили на ободе грузик массой
с горизонтально расположенной осью прикрепили на ободе грузик массой 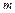 . Найти массу колеса
. Найти массу колеса 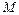 , предполагая ее однородно распределенной по ободу, если частота малых колебаний колеса вокруг оси равна
, предполагая ее однородно распределенной по ободу, если частота малых колебаний колеса вокруг оси равна 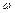 .
.
Решение
Будем характеризовать положение колебательной системы при помощи угла отклонения радиуса колеса, проведенного через грузик, от вертикального направления. Полная механическая энергия системы складывается из кинетической энергии колеса и груза и потенциальной энергии груза.
Кинетическая энергия может быть выражена через угол отклонения по формуле
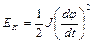 ,
,
где 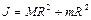 - момент инерции системы.
- момент инерции системы.
Потенциальная энергия груза выражается через угол отклонения по формуле
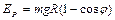 .
.
Из закона сохранения энергии следует
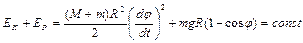 .
.
Дифференцируя это уравнение по времени, получаем
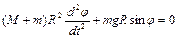 .
.
Рассматривая случай малых колебаний 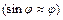 , получаем
, получаем
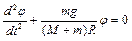 . (1.6.8)
. (1.6.8)
Таким образом, для частоты малых колебаний из (1.6.8) следует
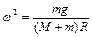 . (1.6.9)
. (1.6.9)
Выражая из полученной формулы массу колеса, находим
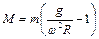 .
.
Задача 4. Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями 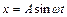 ,
, 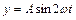 . Определить уравнение траектории точки.
. Определить уравнение траектории точки.
Решение
Воспользуемся тригонометрической формулой синуса двойного угла
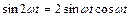 . (1.6.10)
. (1.6.10)
Выразим из уравнения горизонтального движения 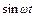 и воспользуемся основным тригонометрическим тождеством:
и воспользуемся основным тригонометрическим тождеством:
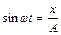 ,
, 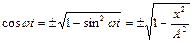 . (1.6.11)
. (1.6.11)
Подставляя (1.6.11) в (1.6.10) и затем – в уравнение вертикального движения, получаем
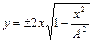 ,
,
или, после возведения в квадрат,
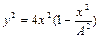 .
.
 2015-05-13
2015-05-13 5663
5663
