МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
БАШКИРСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
Методические указания к выполнению лабораторной работы № 12 по электричеству
ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ И ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДИНАМИЧЕСКОЙ ПОСТОЯННОЙ С ПОМОЩЬЮ ТАНГЕНС-ГАЛЬВАНОМЕТРА
УФА – 2009
Печатается по решению кафедры общей физики
от 1 июля 2009г., протокол №6
Составители:
ИССЛЕДОВАНИЕ МАГНИТНОГО ПОЛЯ ЗЕМЛИ И ОПРЕДЕЛЕНИЕ ЭЛЕКТРОДИНАМИЧЕСКОЙ ПОСТОЯННОЙ С ПОМОЩЬЮ ТАНГЕНС-ГАЛЬВАНОМЕТРА.
Цель работы: изучение устройства и принципов работы тангенс-гальванометра, Определение горизонтальной составляющей магнитного поля Земли, определение электродинамической постоянной.
Приборы и принадлежности: тангенс – гальванометр, источники постоянного и переменного тока, вольтметр, амперметр, батарея конденсаторов.
Краткая теория.
Наша планета, подобно гигантскому магниту, обладает магнитным полем (земной магнетизм или геомагнетизм).
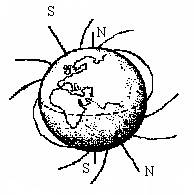 Земля в целом представляет собой огромный шаровый магнит. В любой точке пространства, окружающего Землю, и на ее поверхности обнаруживается действие магнитных сил. Иными словами, в пространстве, окружающем Землю, создается магнитное, силовые линии которого изображены на рисунке. Северный магнитный полюс N находится на южном географическом S и наоборот.
Земля в целом представляет собой огромный шаровый магнит. В любой точке пространства, окружающего Землю, и на ее поверхности обнаруживается действие магнитных сил. Иными словами, в пространстве, окружающем Землю, создается магнитное, силовые линии которого изображены на рисунке. Северный магнитный полюс N находится на южном географическом S и наоборот.
Существование магнитного поля в любой точке Земли можно установить с помощью магнитной стрелки. Если подвесить магнитную стрелку NS на нити Lтак, чтобы точка подвеса совпадала с центром тяжести стрелки, то стрелка становится по направлению касательной к силовой линии магнитного поля Земли. В северном полушарии – южный конец будет наклонён к Земле и стрелка составит с горизонтом угол наклонения θ (на магнитном экваторе наклонение θ равно 0). Вертикальная плоскость, в которой расположится стрелка, называется плоскостью магнитного меридиана. Все плоскости магнитных меридианов пересекаются по прямой NS, а следы магнитных меридианов на поверхности Земли сходятся в магнитных полюсах N и S. Так как магнитные полюса не совпадают с географическими полюсами, то стрелка будет отклонена от географического меридиана. Угол который образует вертикальная плоскость, проходящая через стрелку (т.е. магнитный меридиан) с географическим меридианом, называется магнитным склонением α.
Существующие в настоящее время теории Земного магнетизма можно разбить на две группы:
Теории, объясняющие наличие магнитного поля электрическими токами, циркулирующими на больших глубинах в жидком ядре Земли.
Теории, основанные на предположении, что земная кора содержит в разных своих участках различное количество магнитных пород.
Однако происхождение магнитного поля Земли в настоящее время ещё не выяснено
Характеристикой магнитного поля Земли, как и всякого магнитного поля, служит вектор магнитной индукции 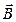 и его составляющие. Для разложения вектора
и его составляющие. Для разложения вектора 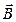 на составляющие обычно принимают прямоугольную систему координат, в которой ось
на составляющие обычно принимают прямоугольную систему координат, в которой ось  ориентируют по направлению географического меридиана, а ось
ориентируют по направлению географического меридиана, а ось  – по направлению параллели, при этом положительным считается направление оси
– по направлению параллели, при этом положительным считается направление оси 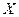 к северу, а оси
к северу, а оси  - к востоку. Третья ось
- к востоку. Третья ось 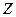 в таком случае примет вертикальное положение.
в таком случае примет вертикальное положение.
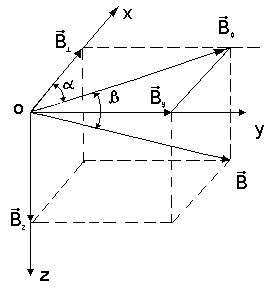
рис. 1
На рис. 1 изображен вектор 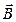 и его проекции на координатные оси и плоскость XY. Проекция этого вектора на ось X северной составляющей и обозначается
и его проекции на координатные оси и плоскость XY. Проекция этого вектора на ось X северной составляющей и обозначается 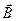 X
X  , проекция на ось Y называется восточной составляющей
, проекция на ось Y называется восточной составляющей 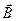 Y и проекция на ось Z вертикальной составляющей
Y и проекция на ось Z вертикальной составляющей 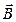 Z.
Z.
Проекция 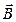 на плоскость XOY называется горизонтальной составляющей магнитной индукции поля Земли:
на плоскость XOY называется горизонтальной составляющей магнитной индукции поля Земли: 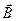

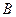 с
с  =
= 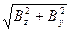

Плоскость 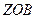 , в которой лежит вектор
, в которой лежит вектор 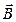 , называется плоскостью магнитного меридиана, а угол
, называется плоскостью магнитного меридиана, а угол 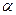 между этой плоскостью и плоскостью
между этой плоскостью и плоскостью 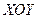 – магнитным отклонением.
– магнитным отклонением.
Склонение, наклонение, горизонтальная составляющая, а также составляющие: северная, восточная и вертикальная – называются элементами Земного магнетизма.
Определение горизонтальной составляющей 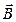 0 удобно сделать с помощью так называемого ТАНГЕНС-ГАЛЬВАНОМЕТРА, устройство которого показано на рис. 2.
0 удобно сделать с помощью так называемого ТАНГЕНС-ГАЛЬВАНОМЕТРА, устройство которого показано на рис. 2.
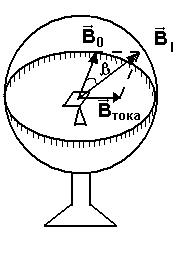
рис. 2
Рассмотрим круговой проводник, радиуса 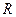 состоящий из
состоящий из 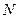 витков, расположенных в вертикальной плоскости геомагнитного меридиана. В центре кругового проводника поместим магнитную стрелку, вращающийся вокруг вертикальной оси. Если по катушке пропустить ток
витков, расположенных в вертикальной плоскости геомагнитного меридиана. В центре кругового проводника поместим магнитную стрелку, вращающийся вокруг вертикальной оси. Если по катушке пропустить ток 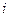 , то возникает магнитное поле индукции
, то возникает магнитное поле индукции 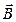 тока, направленное перпендикулярно к плоскости катушки.
тока, направленное перпендикулярно к плоскости катушки.
Таким образом, на магнитную стрелку будут действовать две взаимно перпендикулярные составляющие индукции: магнитного поля Земли и магнитного поля тока. Магнитная стрелка отклоняется на угол β, то есть устанавливается по направлению равнодействующей 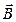 i, - по диагонали параллелограмма, сторонами которого будут
i, - по диагонали параллелограмма, сторонами которого будут 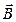 тока и
тока и 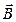 0
0
Легко видеть, что
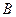 тока =
тока = 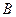 0
0 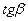 ,
, 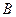 тока=
тока= 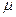 0
0 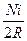 , (1)
, (1)
Поэтому:
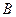 0=
0= 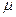 0
0 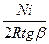 =
= 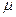 0
0 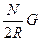 (2)
(2)
Где 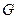 – постоянная (для данной точки Земли) тангенс гальванометра.
– постоянная (для данной точки Земли) тангенс гальванометра.
Следует помнить, что (2) является приближенной, т. е. верной только в том случае, когда размер магнитной стрелки много меньше радиуса 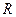 кругового тока. В противном случае конечная длина стрелки требует внесения определенных поправок. Можно показать, что если магнитная стрелка помещается в центре кругового тока, а на расстоянии
кругового тока. В противном случае конечная длина стрелки требует внесения определенных поправок. Можно показать, что если магнитная стрелка помещается в центре кругового тока, а на расстоянии 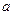 от него, то в этом случае поле
от него, то в этом случае поле
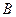 тока =
тока = 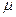 0
0 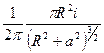 .
.
Ниже будет показано, что самое благоприятное для измерений значение угла 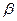 будет в том случае, когда этот угол близок к
будет в том случае, когда этот угол близок к 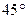 .
.
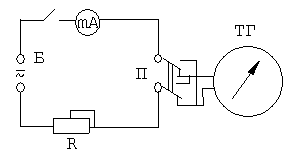
рис. 3.
Схема установки приведена на рис. 3.
Б – источник напряжения,
R – реостат,
MA – миллиамперметр,
П – переключатель напряжения тока в тангенс – гальванометр,
ТГ – тангенс – гальванометр
Определение горизонтальной составляющей магнитного поля Земли.
· Собрать схему на рис. 3;
· Поворачивая подставку гальванометра, установить его катушку так, чтобы она лежала в плоскости геомагнитного меридиана:
· Включают ток в обмотку тангенс – гальванометра, и измеряя его величину с помощью реостата 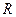 , добиваются поворота стрелки на угол
, добиваются поворота стрелки на угол 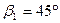 , фиксируют это значение тока i1. Затем меняют положение переключателя П, вновь добиваются поворота стрелки на угол 45˚, фиксируют значение тока i2.
, фиксируют это значение тока i1. Затем меняют положение переключателя П, вновь добиваются поворота стрелки на угол 45˚, фиксируют значение тока i2.
· Рассчитывают это значение тока 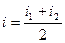 и вычисляют по (2) значение
и вычисляют по (2) значение 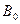 (в Тл). Полагая
(в Тл). Полагая 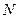 = 100 витков,
= 100 витков, 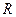 = 10,25 см;
= 10,25 см;
· Оценивают по (3) максимальную погрешность измерения 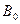 , считая что значение
, считая что значение 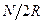 известно точно, а абсолютная погрешность
известно точно, а абсолютная погрешность 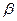 не превышает половины деления лимба и относительная погрешность в измерении тока определяется лишь классом точности миллиамперметра.
не превышает половины деления лимба и относительная погрешность в измерении тока определяется лишь классом точности миллиамперметра.
Поскольку катушку тангенс – гальванометра трудно точно установить в направлении север – юг. Можно производить измерение 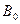 без предварительной ориентировки катушки, фиксируя углы
без предварительной ориентировки катушки, фиксируя углы 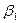 и
и 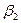 от начального положения для обоих направлений тока определенной величины.
от начального положения для обоих направлений тока определенной величины.
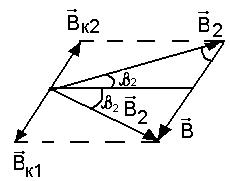
рис. 4.
Из рис. 4 видно, что:
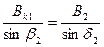 ;
; 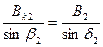 ;
; 
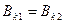 ; (3)
; (3)
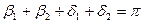 ;
; 
где 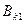 и
и 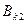 – индукция поля катушки при различных направлениях тока в ней.
– индукция поля катушки при различных направлениях тока в ней.
Решение (3) дает:
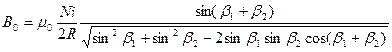 (4)
(4)

пользуясь (4) можно определить 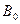 без предварительной ориентировки катушки тангенс – гальванометра;
без предварительной ориентировки катушки тангенс – гальванометра;
- воспользовавшись формулой (4) определить значение 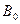 без предварительной ориентировки катушки тангенс – гальванометра. Измерения произвести при нескольких значениях тока в цепи катушки (3 – 4 значения) и по полученным значениям
без предварительной ориентировки катушки тангенс – гальванометра. Измерения произвести при нескольких значениях тока в цепи катушки (3 – 4 значения) и по полученным значениям 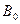 определить ее среднеарифметическую величину;
определить ее среднеарифметическую величину;
- вывести условие, при котором наиболее выгодно производить измерение 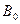 , получив формулу:
, получив формулу:
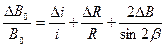 (5)
(5)
Определение электростатической постоянной с помощью тангенс-галльванометра.
Основными е6диницами в системе CGSE являются 1 см, 1 г и 1 с. Количество электричества (заряд) в этой системе определяется из закона Кулона:
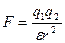 , (6)
, (6)
где 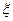 - диэлектрическая проницаемость среды (в CGSE – величина безразмерная).
- диэлектрическая проницаемость среды (в CGSE – величина безразмерная).
За единицу заряда в системе CGSE принимается такой заряд, который взаимодействует в вакууме (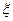 = 1) с равным по величине зарядом, находящимся на расстоянии 1 см, с силой в 1 дин =10-5 Н.
= 1) с равным по величине зарядом, находящимся на расстоянии 1 см, с силой в 1 дин =10-5 Н.
Из (6) следует, что размерность заряда:
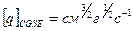 .
.
Поскольку ток определяется количеством электричества, прошедшим через поперечное сечение проводника за 1 с (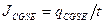 ), его размерность равна:
), его размерность равна:
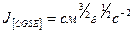
Непосредственное измерение тока в системе CGSE затруднено, поэтому в данном упражнении величина 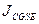 определяется путем измерения емкости конденсатора
определяется путем измерения емкости конденсатора 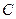 и разности потенциалов
и разности потенциалов 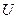 на его обкладках.
на его обкладках.
За единицу разности потенциалов в соответствии с формулой 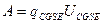 принимается разность потенциалов между двумя точками, перемещение единичного заряда между которыми сопровождается затратой работы в 1 Эрг. Размерность разности потенциалов:
принимается разность потенциалов между двумя точками, перемещение единичного заряда между которыми сопровождается затратой работы в 1 Эрг. Размерность разности потенциалов:
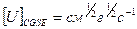 .
.
За единицу емкости [C]... принимается емкость проводника, при сообщении которому заряда в 1 ед. CGSE [ x] потенциал проводника изменяется на 1 ед. CGSE [U] размерность емкости 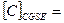 см.
см.
Основными единицами системы CGSM являются 1 см, 1 г, 1 с. Ток в этой системе определяется на основе определения силы взаимодействия двух бесконечных длинных параллельных проводников:
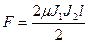 , (7)
, (7)
где 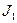 и
и 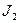 - токи в проводниках,
- токи в проводниках,
r – расстояние между ними.
l – отрезок проводника, на которой рассчитывается сила,
m - магнитная проницаемость среды (безразмерная вeличина в CGSM).
За единицу тока в CGSM принимают такой ток, который, протекая по двум параллельным проводникам бесконечной длины и ничтожно малого поперечного сечения, расположенным на расстоянии 2 см друг от друга в вакууме (m = 1), вызывает силу взаимодействия между ними, равную 1 дине на 1 см длины проводника.
Из (7) следует, что размерность силы тока:
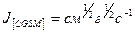 .
.
Точные эксперименты, проведенные Вебером В. и Кольраушем Ф. (1856 г.), Столетовым А. Г. (1876 г.), Эйхенвальдом А. А. (1901 г.) показали, что отношение единиц силы тока в системах CGSE и CGSM численно равно: 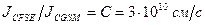 ,
,
Где 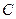 – электростатическая постоянная, размерность, которой равна:
– электростатическая постоянная, размерность, которой равна:
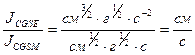
Таким образом, электродинамическая постоянная совпадает со скоростью света в вакууме не только по абсолютной величине, но имеет размерность скорости. Численное значение 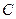 может быть определено, если ток одной и той же величины измерять в обеих системах единиц. В данной работе ток в системе CGSM будем измерять с помощью тангенс – гальванометра, а в системе CGSE - косвенным путем. Наблюдая разряд конденсатора.
может быть определено, если ток одной и той же величины измерять в обеих системах единиц. В данной работе ток в системе CGSM будем измерять с помощью тангенс – гальванометра, а в системе CGSE - косвенным путем. Наблюдая разряд конденсатора.
Из (8) следует, для выражения одного и того же тока в системе CGSE используется число, которое в 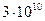 раз больше, чем для выражения того же тока в системе CGSM.
раз больше, чем для выражения того же тока в системе CGSM.
Следовательно, единица тока системы CGSE: в 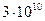 раз меньше единицы тока системы CGSM:
раз меньше единицы тока системы CGSM:
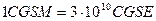
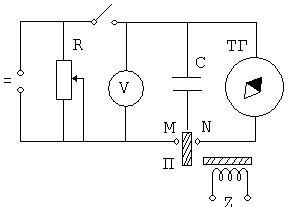
рис. 5.
На рис. 5 показана принципиальная схема для определения величины 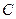 . Электромагнитный прерыватель П попеременно замыкает контакты M и N, тем самым заряжает конденсатор
. Электромагнитный прерыватель П попеременно замыкает контакты M и N, тем самым заряжает конденсатор 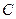 и разряжает его через обмотку тангенс – гальванометра ТГ. Напряжение на пластинках конденсатора измеряется вольтметром
и разряжает его через обмотку тангенс – гальванометра ТГ. Напряжение на пластинках конденсатора измеряется вольтметром 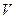 . Подаваемое напряжение регулируется потенциометром
. Подаваемое напряжение регулируется потенциометром 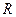 .
.
Если конденсатор емкостью 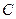 , заряженный до потенциала
, заряженный до потенциала 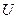 разрядить через витки тангенс – гальванометра. То через них протечет заряд
разрядить через витки тангенс – гальванометра. То через них протечет заряд 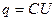 . Если
. Если 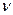 раз в секунду последовательно заряжать конденсатор от источника тока и разряжать через витки гальванометра, то через них протечет заряд
раз в секунду последовательно заряжать конденсатор от источника тока и разряжать через витки гальванометра, то через них протечет заряд 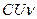 . Средний ток, проходящий через витки, будет равен:
. Средний ток, проходящий через витки, будет равен:
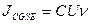 ,
,
где 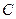 и
и 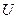 – выражены в системе CGSE.
– выражены в системе CGSE.
Значение тока в системе CGSM определяется с помощью тангенс – гальванометра, если известна горизонтальная составляющая 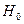 напряженности магнитного поля Земли:
напряженности магнитного поля Земли:
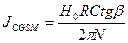 , (10)
, (10)
где 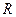 и
и 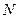 – радиус и число витков катушки тангенс – гальванометра,
– радиус и число витков катушки тангенс – гальванометра,
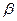 - угол отклонения магнитной стрелки.
- угол отклонения магнитной стрелки.
Величина 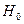 в (10) должна быть выражена в Эрстедах, а радиус
в (10) должна быть выражена в Эрстедах, а радиус 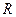 – в см.
– в см.
Из (9) и (10) легко получим:
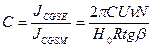 (11)
(11)
Порядок выполнения работы таков:
- собрать схему установки в соответствии с рис. 5;
- установить тангенс – гальванометр так, чтобы его обмотка находилась в плоскости геомагнитного меридиана;
- замкнуть цепь переменного тока и цепь постоянного тока,
- измерить вольтметром напряжение 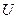 и угла
и угла 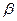 повторяют 3 – 4 раза, всякий раз замыкая и размыкая цепь постоянного тока. Из полученных значений находят среднее.
повторяют 3 – 4 раза, всякий раз замыкая и размыкая цепь постоянного тока. Из полученных значений находят среднее.
- По (11) определяют величину 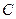 , при этом разность потенциалов
, при этом разность потенциалов 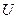 должна быть выражена в системе CGSE. Значение
должна быть выражена в системе CGSE. Значение 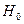 принять равным 0.14 Э.
принять равным 0.14 Э.
- Изменяют направление тока ив обмотке тангенс гальванометра, поменяв метами концы проводников, подходящих к его зажимам. При этом стрелка будет отклоняться в сторону, противоположную отклонению при первом измерении. Снова измеряют угол 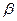 и напряжение
и напряжение 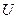 ;
;
- Вычислить среднее значение 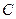 ;
;
- Определить абсолютную и относительную ошибки в определении величины 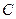 .
.
-
КОНТРОЛЬНЫЕ ВОПРОСЫ:
- рассказать о принципах построения системы единиц CGSE и CGSM,
- определить единицы тока в обеих системах,
- объяснить устройство и принцип действия тангенс – гальванометра,
- дать определение основным элементам земного магнетизма.
ЛИТЕРАТУРА:
Рублев Ю.В., Кортнев А.В., Куценко А.Н. Практикум по электричеству. М.: Высшая школа, 1971.
Гольдин Л.Л. руководство к лабораторным занятиям по физике. М.: Наука, 1973.
Савельев И.В. Курс общей физики. Электричество. М.: Наука, 1987.
Иверонова В.И. физпрактикум. М.: Наука, 1968.
 2015-05-30
2015-05-30 5085
5085






