2015-05-22
4421.1. Дан закон движения x=a cos(wt+j). Найти мгновенную скорость v =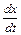 
и ускорение j = 
.
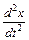1.2. Проверить, что выражение x=a sin(wt+j) является общим решением уравнения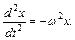 
1.3. Найти общие решения дифференциальных уравнений а) y¢¢– 4 y¢+3y=0 б) y¢¢+ 4 y¢+13y=0.
1.4. Найти общие решения дифференциальных уравнений а) y¢¢–9y=0 б) y¢¢–9y=0 в)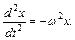
1.5. Найти общее решение дифференциального уравнения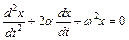 
, где a< w.
Указание. Ввести обозначение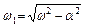 
.
1.6. Точка перемещается вдоль оси Ox под действием силы F= - k x из положения x=x1. в положение x=-x2 Найти работу, которую совершает сила.
1.7. На материальную точку массы m на оси Ox действует сила F=-k x. Составить дифференциальное уравнение движения точки и показать, что величина E=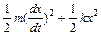 
не зависит от времени. Решить двумя способами.
1.8. Решить задачи Коши
а)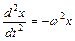 
, 
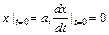. б) ,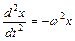 
.
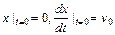1.9. Используя формулу Эйлера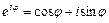 
, доказать, что 
, 
.
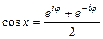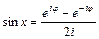1.10. Решить 1.8, используя комплексные частные решения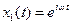 
и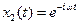 
.
1.11. Дано уравнение 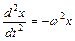. а) Показать, что x= 
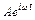, где A – любое комплексное число, удовлетворяет уравнению; б) Пусть A = 
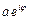. Найти Re x, Im x. Каков физический смысл a, j, A?
1.12. Решить задачу Коши для уравнения радиоактивного распада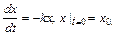 
. Исключить из решения параметр k, считая известным период полураспада T0.
Домашнее задание.
1.13. Сила тока I в цепи из активного сопротивления и самоиндукции удовлетворяет уравнению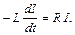 
Зная начальную силу тока I| t=0= I0 , найти зависимость I от времени.
1.14. Решить задачу Коши ,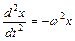 
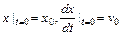. Найти амплитуду колебаний.
1.15. Найти общее решение y(x) уравнения y¢¢+2 y¢+2y=0.
1.16. Найти общее решение y(x) уравнения y¢=-5y.
1.17. Записать в тригонометрической и показательной форме комплексные числа
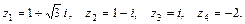
1.18. * Лестница, прислонённая к стене, скользит так, что её нижний конец удаляется от стены со скоростью V1=2м/с. Расстояние её нижнего конца от стены в данный момент равно 3м, а расстояние верхнего конца от пола равно 4м. Какова в данный момент скорость верхнего конца?
x=3м/с, y=4 м/с
