Проверка гипотез о средней и о доле

Выборочное наблюдение

Общая характеристика выборочного наблюдения

Ошибки выборки при собственно случайном отборе

Основные способы формирования выборочной совокупности

Определение необходимой численности выборки

Малая выборка

Распространение результатов выборочного наблюдения на генеральную совокупность

Общие понятия и схема статистической проверки гипотез

Проверка гипотез о средней и о доле

Практика применения выборочного метода наблюдения

Приложение 1

Приложение 2

Приложение 3

1. Общая характеристика выборочного наблюдения

Выборочное наблюдение – это такой вид статистического наблюдения, при котором обследованию подвергается не вся изучаемая совокупность, а лишь часть ее единиц, отобранных в определенном порядке. При этом вся исследуемая совокупность называется генеральной, а единицы, подлежащие наблюдению, составляют выборочною совокупность, или выборку. [3. C. 66]

Система правил отбора единиц и способов характеристики изучаемой совокупности исследуемых единиц составляет содержание выборочного метода. Важная роль в формировании выборочного метода наблюдения принадлежит работам Якоба Бернулли (1654-1705). Весомый вклад в разработку теоретических основ выборочного метода внесли русские математики - П. Л. Чебышев, А. М. Ляпунов, А. А. Марков. Российская статистика имеет немалые заслуги в практическом применении выборочного метода. Так уже во второй половине XIX в. выборочные обследования проводились земскими статистиками и отличались определенной новизной в решении вопросов организации отбора единиц. При проведении подворной переписи крестьянских хозяйств Пензенской губернии 1909-1911 г.г. был использован метод сочетания звеньев выборочного обследования разной подробности, впоследствии названный многофазным отбором. В ряде обследований использовалась гнездовая выборка, в других - сплошное обследование сочеталось с механическим отбором единиц для контроля полученных данных, например, при Всероссийской переписи населения 1916 г. Теория выборочного метода получила развитие в трудах известного русского статистика А. А. Чупрова и в работе А. Г. Ковалевского «Основы теории выборочного метода», вышедшей в 1924 г. Классификацию форм выборочного наблюдения дали в 1930 г. известные отечественные статистики А. Я. Боярский и Б. С. Ястремский.

В последние годы выборочные обследования стали широко применяться в работе органов государственной статистики. Крупные и средние предприятия охватываются сплошным наблюдением за их деятельностью, а наблюдение за деятельностью малых предприятий производится с помощью выборочных обследований. В ряде случаев выборочные наблюдения применяются в сочетании со сплошными переписями и учетами. Например, программа Всероссийской переписи населения 2002 г. содержит как вопросы сплошного наблюдения, относящиеся ко всему населению, так и вопросы выборочного наблюдения 25% населения для характеристики основного занятия, положения в занятии, места работы, а также вопросы 5%-ного выборочного обследования с целью изучения брачности и рождаемости.

Применение выборочного наблюдения взамен сплошного дает возможность лучше организовать наблюдение, обеспечивает быстроту проведения наблюдения, приводит к экономии средств и затрат труда на получение и обработку информации. Объективную гарантию репрезентативности полученной выборочной совокупности дает применение соответствующих научно обоснованных способов отбора подлежащих обследованию единиц. В процессе формирования выборочной совокупности должен быть обеспечен строго объективный подход к отбору единиц. Нарушение этого принципа, когда наблюдению подвергаются единицы, отобранные на основании субъективного мнения исследователя, приводит к тому, что результаты такого наблюдения относятся не ко всей генеральной совокупности, а только к той ее части, которая была подвергнута наблюдению.

В сравнении с другими видами несплошных наблюдений преимущество выборочного наблюдения заключается в том, что по результатам этого наблюдения можно оценить искомые параметры генеральной совокупности. Между характеристиками выборочной совокупности и искомыми характеристиками (параметрами) генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой. Общая величина возможной ошибки выборочной характеристики слагается из ошибок двоякого рода: ошибки регистрации и ошибки репрезентативности.

Ошибки регистрации свойственны любому статистическому наблюдению вообще и появление их может быть вызвано несовершенством измерительных приборов, недостаточной квалификацией наблюдателя, неточностью подсчетов и т.п. Можно полагать, что по сравнению со сплошными наблюдениями опасность возникновения ошибок регистрации при проведении выборочных наблюдений должна быть меньше, так как выборочные наблюдения проводятся с участием более квалифицированных работников и, следовательно, более тщательно. Значительно уменьшается при выборочном наблюдении и опасность преднамеренных искажений данных, так как специально подобранные и обученные наблюдатели в них не заинтересованы.

Ошибки репрезентативности присущи только несплошным наблюдениям и представляют собой расхождение между величиной полученных по выборке показателей и величиной этих показателей, которые были бы получены при проведенном с одинаковой степенью точности сплошном наблюдении.

Ошибки репрезентативности могут быть систематическими и случайными. Систематические ошибки могут возникать в связи с особенностями принятой системы отбора и обработки данных наблюдений или в связи с нарушением установленных правил отбора. [2. C. 157]

Случайные ошибки репрезентативности неизбежно возникают при проведении выборочных обследований, так как обеспечить абсолютную адекватность характеристик выборочной и генеральной совокупности даже при тщательно спланированном наблюдении практически невозможно. Оценка таких ошибок — одна из задач статистики. Важно определить не только абсолютную величину ошибки, но и ее допустимый уровень. Стремление максимально уменьшить случайную ошибку выборки приводит к росту ее объема, а большая ошибка ставит под сомнение возможность практического использования полученных результатов. Допустимый уровень ошибки должен быть установлен при разработке программы обследования.

Основные этапы выборочного наблюдения:

1) определение цели, задач и составление программы наблюдения;

2) анализ информационных источников, используемых для выделения генеральной совокупности объектов наблюдения (основы выборки);

3) формирование генеральной совокупности дли проведения выборочного обследования;

4) разработка методологии формирования выборочной совокупности, включающей выбор способа отбора, определение необходимого объема выборки, этапов отбора единиц из генеральной совокупности, планирование и проведение пробной выборки;

5) формирование выборки;

6) сбор данных на основе разработанной программы;

7) анализ полученных результатов и расчет основных характеристик выборочной совокупности;

8) расчет ошибок выборки и распространение ее результатов на генеральную совокупность. [4. C. 151]

Представление о статистических данных, как о выборочных, может относиться не только к собственно выборке, но и к данным сплошного наблюдения, которые иногда рассматриваются как выборка из всех возможных реализаций изучаемого процесса. Это имеет смысл в случае малого числа единиц совокупности. Кроме того, трактовка данных как выборочных используется применительно к результатам эксперимента, которые рассматриваются как некая выборка из потенциально бесконечного числа повторений экспериментальных наблюдений.

Трактовка данных как выборочных является основой деления статистики на описательную (дескриптивную) и выводную.

Методы описательной статистики включают сбор данных по всем единицам изучаемой совокупности, их обработку, получение сводных показателей, которые характеризуют только наблюдаемую совокупность. Например, если наша задача состоит в изучении успеваемости группы студентов, включающей 25 человек, то вычисленный средний балл по этой группе, процент отличных оценок и т.д. являются описаниями данной совокупности. Если же мы будем рассматривать эту группу студентов с точки зрения оценки успеваемости всех студентов данного колледжа или университета, то эта группа предстанет как выборка из общего числа студентов. В таком случае средний балл для группы будет являться оценкой средней успеваемости студентов колледжа в целом.

Генеральная совокупность может быть реальной, а может быть гипотетической, включающей случаи, которые реально не существуют, например, все возможные результаты эксперимента.

В выводной статистике принято строго различать параметры и свойства генеральной совокупности и их оценки по данным выборки. С этой целью принята следующая система обозначений: генеральные параметры обозначаются греческими буквами, выборочные показатели, которые рассматриваются как оценки генеральных параметров, — латинскими буквами.

Таблица 1.1

Условные обозначения

Показатель	Совокупность
генеральная	выборочная
Объем (число единиц) совокупности	N	n
Среднее значение признака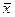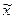
Доля единиц, обладающих изучаемым признаком	p	w
Доля единиц, не обладающих изучаемым признаком	q	1 - w
Дисперсия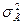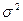
Среднее квадратическое отклонение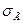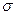

Объем генеральной совокупности обозначают N, объем выборочной совокупности — n.

Выборочные оценки отличаются от генеральных параметров за счет ошибки наблюдения и ошибки выборки:

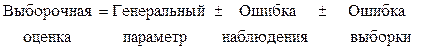
Подводя итоги, можно сказать, что описательная статистика является инструментом описания совокупности, по которой у нас полностью имеются исходные данные.

Метод статистического вывода позволяет по данным выборок делать заключение о большей совокупности, по которой мы не имеем исчерпывающих наблюдений. [1. C. 217]

2. Ошибки выборки при собственно случайном отборе

Виды случайного отбора

Теоретические основы выборочного метода, первоначально разработанные применительно к собственно случайному отбору, используют и для определения ошибок выборки при других способах наблюдения.

Рассмотрим наиболее простой способ формирования выборочной совокупности — собственно случайный отбор.

Собственно случайный отбор может быть повторным и бесповторным. При повторном отборе каждая единица, отобранная в случайном порядке из генеральной совокупности, после проведения наблюдения возвращается в эту совокупность и может быть вновь подвергнута обследованию. На практике такой способ отбора встречается редко. Гораздо более распространен собственно случайный бесповторный отбор, при котором обследованные единицы в генеральную совокупность не возвращаются и не могут быть обследованы повторно. При повторном отборе вероятность попадания в выборку для каждой единицы генеральной совокупности остается неизменной. При бесповторном отборе она меняется, но для всех единиц, оставшихся в генеральной совокупности после отбора из нее нескольких единиц, вероятность попадания в выборку одинакова.

Для обеспечения случайности отбора используются разные способы. Если параметры генеральной совокупности известны и все ее единицы могут быть пронумерованы, то случайный отбор обеспечивается с помощью жребия. При большом объеме совокупности выборка может осуществляться с использованием таблиц случайных чисел. Такие таблицы представляют собой набор четырех- или пятизначных чисел. Если число единиц в генеральной совокупности трехзначное, то из любого столбца или строки таблицы последовательно выписывают столько чисел, сколько единиц в выборочной совокупности. От каждого числа отбрасывают первую или последнюю цифру (или две цифры, если таблицы состоят из пятизначных чисел). Затем отбирают числа, не превышающие число единиц в генеральной совокупности.

Пример. В первом столбце таблицы случайных чисел содержатся числа: 5489, 3522, 7555, 5759, 6303 и т.д. Предположим, что генеральная совокупность состоит из 600 единиц. При этом в соответствии с программой выборки должно быть обследовано 30 единиц. Номера единиц, попавших в выборку: 489, 522, 555, 303 и т.д. Единицы с номером 759 в генеральной совокупности нет, поэтому в выписанные порядковые номера единиц наблюдения это число не попадает.

Ошибки выборки при случайном повторном отборе

Ошибка выборки для средней. Основные свойства выборочной совокупности, сформированной методом собственно случайного повторного отбора, рассмотрим на следующем примере.

Пример. Из генеральной совокупности (например, студенты I курса, данные о возрасте которых приведены в табл. 2.1) с числом единиц N = 4 методом собственно случайного повторного отбора осуществлена выборка, объем которой равен 2 единицам, т.е. n = 2.

Таблица 2.1

Порядковый номер студента
Возраст xi, лет

Результаты всех возможных испытаний представлены в табл. 2.2

Таблица 2.2

Номера отобранных единиц	Выборочная средняя	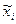Номера отобранных единиц	Выборочная средняя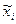
1 и 1	16,0	3 и 1	16,5
1и 2	16,5	3 и 2	17,0
1 и 3	16,5	3 и 3	17,0
1 и 4	17,0	3 и 4	17,5
2 и 1	16,5	4 и 1	17,0
2 и 2	17,0	4 и 2	17,5
2 и 3	17,0	4 и 3	17,5
2 и 4	17,5	4 и 4	18,0

В генеральной совокупности средний возраст студентов

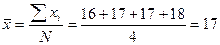лет,

Дисперсия изучаемого признака

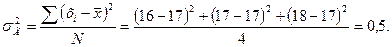
На основе результатов расчета 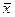и 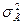можно построить распределение полученных значений выборочных средних (табл. 2.3).

Таблица 2.3

i	Средний возраст студентов в выборке, лет	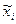Отклонение выборочной средней от генеральной средней	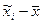Частота появления i -го значения выборочной средней	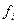Вероятность появления i-го значения выборочной средней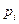
	16,0	-1,0		0,0625
	16,5	-0,5		0,2500
	17,0	0,0		0,3750
	17,5	0,5		0,2500
	18,0	1,0		0,0625
Итого	-		1,0000

Вероятности появления различных значений выборочной средней, равные вероятностям соответствующего отклонения выборочной средней от генеральной средней, неодинаковы. Чем больше отклонение выборочной характеристики от генеральной, тем меньше вероятность его появления. Наиболее часто оценка, полученная на основе выборки, совпадает с соответствующей характеристикой генеральной совокупности. В приведенном примере вероятность появления в выборке среднего возраста студентов, равного 17 годам, наиболее велика (p3 = 0,3750). Рассчитаем математическое ожидание выборочной средней:

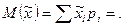16,0·0,0625+16,5·0,25+17,0·0,375+17,5·0,25+18,0·0,0625=17 лет.

Таким образом, 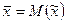, т.е. выборочная средняя является несмещенной оценкой генеральной средней. Аналогичный результат можно получить, используя вместо вероятности p1 частоту появления соответствующих значений выборочных средних:

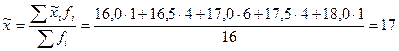лет.

Отклонение выборочной средней от генеральной равно нулю лишь в 6 выборках из 16. В остальных случаях значения выборочной и генеральной средней не совпадают, при этом вероятность появления наибольшего по абсолютной величине отклонения, равного единице, минимальна. Таким образом, существует предел, к которому стремится отклонение выборочной средней от генеральной.

Рассчитаем среднюю величину этих отклонений. Учитывая, что сумма отклонений, взятая в абсолютном выражении, равна нулю, указанную среднюю рассчитаем как среднее квадратическое отклонение:

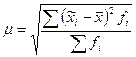
Так как 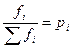, то

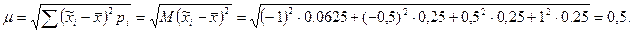
Полученная величина μ называется средней ошибкой выборки. Средняя ошибка выборки — это среднее квадратическое отклонение всех возможных значений выборочной средней от генеральной средней, т.е. от своего математического ожидания.

Дисперсия возможных значений выборочной средней

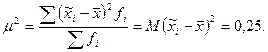
В математической статистике доказано, что эта величина в n раз меньше дисперсии в генеральной совокупности. В данном примере дисперсия в генеральной совокупности 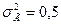, а объем выборки n = 2, тогда

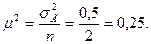
Следовательно, средняя выборка может быть определена по формуле:

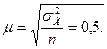
При собственно случайном повторном отборе средняя ошибка выборки зависит от:

вариации изучаемого признака в генеральной совокупности;

объема выборки.

Чем больше вариация признака, тем больше ошибка выборки. Для ее уменьшения необходимо увеличить объем выборочной совокупности.

В действительности решается обратная задача: на основе выборочных данных делается вывод о некоторых характеристиках генеральной совокупности. Согласно правилу сложения дисперсий дисперсия в генеральной совокупности 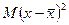может быть представлена как сумма двух слагаемых: средней величины из отклонений отдельных значений от выборочных средних 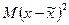и средней величины из отклонений выборочных средних от генеральной средней 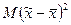, т.е.

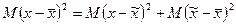
Учитывая, что 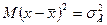, , 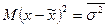а 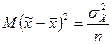, получаем

,

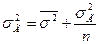или

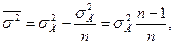
где 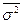- средняя дисперсия выборочных совокупностей.

Следовательно,

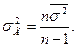
В таком случае средняя ошибка выборки

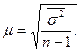(2.1)

Так как все возможные значения дисперсии в выборочной совокупности неизвестны, при нахождении средней ошибки выборки вместо 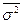в формуле (1) используют дисперсию конкретной выборки 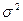. При такой замене велика вероятность малой погрешности. При достаточно большом объеме выборочной совокупности в формуле (2.1) вместо (n – 1) можно использовать величину n. Таким образом, средняя ошибка выборки при собственно случайном повторном отборе будет рассчитываться по формуле:

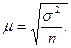(2.2)

Учитывая, что на основе выборочного обследования нельзя точно оценить изучаемый параметр генеральной совокупности, необходимо найти пределы, в которых он находится. В конкретной выборке разность 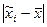может быть больше, меньше или равна µ. Каждое из отклонений 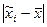от µ имеет определенную вероятность. При выборочном обследовании реальное значение 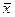в генеральной совокупности неизвестно. Зная среднюю ошибку выборки, с определенной вероятностью можно оценить отклонение выборочной средней от генеральной и установить пределы, в которых находится изучаемый параметр (в данном случае средняя) в генеральной совокупности. Отклонение выборочной характеристики от генеральной называется предельной ошибкой выборки Δ. Она определяется в долях средней ошибки с заданной вероятностью, т.е.

Δ = tµ (2.3)

где t - коэффициент доверия, зависящий от вероятности, с которой определяется предельная ошибка выборки.

Вероятность появления определенной ошибки выборки находят с помощью теорем теории вероятностей. Согласно теореме П.Л. Чебышёва, при достаточно большом объеме выборки и ограниченной дисперсии генеральной совокупности вероятность того, что разность между выборочной средней и генеральной средней будет сколь угодно мала, близка к единице:

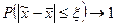при .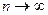

A.M. Ляпунов доказал, что независимо от характера распределения генеральной совокупности при увеличении объема выборки распределение вероятностей появления того или иного значения выборочной средней приближается к нормальному распределению. (Это так называемая центральная предельная теорема.) Следовательно, вероятность отклонения выборочной средней от генеральной средней, т.е. вероятность появления заданной предельной ошибки, также подчиняется указанному закону и может быть найдена как функция от t с помощью интеграла вероятностей Лапласа:

,

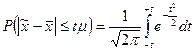где 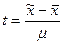- нормированное отклонение выборочной средней от генеральной средней.

Значения интеграла Лапласа для разных t рассчитаны и приводятся в специальных таблицах (см. Приложение 1).

Поясним графически процедуру нахождения вероятности t-кратного отклонения генеральной средней 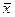от выборочной 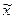(рис.2.1).

Вероятность t-кратного отклонения

.

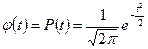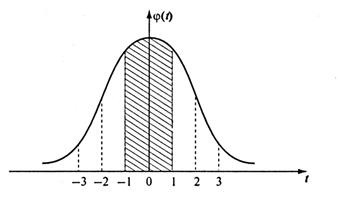
Рис. 2.1. Кривая нормального распределения

Площадь, ограниченная кривой нормального распределения и осью абсцисс, равна суммарной вероятности возникновения различных отклонений 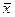от 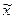, т.е. равна 1. Заштрихованная часть (см. рис. 2.1), которая находится в пределах от - 1 до +1, равна 0,683, т.е. с вероятностью 68,3% можно гарантировать, что отклонение генеральной средней от выборочной не превысит однократной средней ошибки выборки. С этой вероятностью можно утверждать, что среднее значение признака в генеральной совокупности находится в пределах .

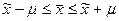Вероятность того, что отклонение средней в генеральной совокупности от выборочной средней не выйдет за пределы 2µ (т.е. t = 2), равна 0,954, а вероятность того, что оно не выйдет за пределы 3µ, — соответственно 0,997. Таким образом, зная среднее значение признака в выборке, можно почти достоверно утверждать, что в генеральной совокупности соответствующее значение будет находиться в пределах 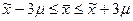. На практике доверительная вероятность принимается чаще всего на уровне 0,95 или 0,99. Соответствующие значения коэффициента доверия равны 1,96 и 2,58 (см. Приложение 1).

Пользуясь приведенными рассуждениями, можно определить вероятность только верхнего или нижнего предела для искомой характеристики генеральной совокупности. Например, вероятность того, что средняя в генеральной совокупности не превысит

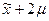, будет равна .

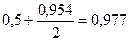Ошибка выборки для доли. Для того чтобы на основе результатов выборочного наблюдения найти долю единиц, обладающих изучаемым признаком в генеральной совокупности, используют формулы, аналогичные приведенным ранее. Дисперсия для доли в генеральной совокупности 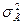равна произведению pq, где р -доля единиц, обладающих изучаемым признаком в генеральной совокупности, a q = 1 – р - доля единиц, не обладающих изучаемым признаком. Так как наблюдение выборочное и величины p и q неизвестны, в формуле средней ошибки выборки используются соответствующие значения, полученные на основе выборочного обследования. Средняя ошибка выборки для доли при собственно случайном повторном отборе рассчитывается по формуле

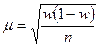, (2.4)

где w –доля единиц, обладающих изучаемым признаком в выборочной совокупности;

(1 – w)- доля единиц в выборке, не обладающих изучаемым признаком.

Предельная ошибка выборки в этом случае определяется так же, как и для средней: Δ = t µ.

Частный случай теоремы П.Л. Чебышёва для доли доказан Я. Бернулли: при достаточно большом объеме выборки вероятность того, что расхождение между долями единиц, обладающих изучаемым признаком, в выборочной и генеральной совокупности будет сколь угодно малым, стремится к единице. При этом распределение вероятностей различных отклонений доли в выборочной совокупности от доли в генеральной также подчиняется нормальному закону. Зная долю в выборочной совокупности, с соответствующей вероятностью можно гарантировать, что доля в генеральной совокупности не выйдет за пределы .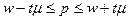

Ошибки выборки при случайном бесповторном отборе

Приведенные ранее формулы средней ошибки выборки справедливы только при повторном отборе. Однако на практике чаще используется бесповторный отбор: обследованная единица не возвращается в генеральную совокупность и не может быть обследована повторно. При этом принцип независимости испытаний нарушается. Очевидно, что при бесповторном отборе из четырех студентов двоих (см. табл. 2.1) средний возраст студентов I курса не может быть равен 16 и 18 годам. Следовательно, средняя ошибка выборки будет меньше.

Средняя ошибка выборки при собственно случайном бесповторном отборе рассчитывается по формуле:

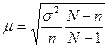. (2.5)

При больших значениях N величину (N – 1) в формуле (5.1) можно заменить на N, тогда упрощенная формула средней ошибки выборки запишется следующим образом:

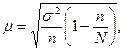(2.6)

для доли

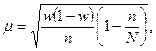(2.7)

где 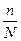- доля обследованных единиц совокупности.

При собственно случайном бесповторном отборе средняя ошибка выборки зависит от:

· вариации изучаемого признака;

· объем выборки;

· доли обследованных единиц.

Чем больше объем выборки и доля обследованных единиц, тем меньше ошибка выборки; вариация признака связана с ней прямо пропорционально.

Если доля обследованных единиц, то дополнительный множитель под знаком радикала практически не влияет на ошибку выборки. В этом случае ошибку выборки при бесповторном отборе можно найти по формулам, которые применяются при повторном отборе.

Наряду с абсолютной величиной средней и предельной ошибок выборки в статистической практике используется относительная их величина, рассчитываемая как отношение ошибки к исследуемому параметру: 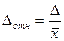или 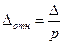. Теоретически в знаменателе должно быть значение исследуемого параметра генеральной совокупности. Однако оно известно, поэтому относительная ошибка рассчитывается через соответствующий параметр выборк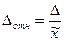и: или 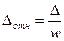. Относительная ошибка выражается в процентах. Выборка считается репрезентативной, если Δотн ≤ 5%.

Пример. По данным выборочного обследования, проведенного Госкомстатом России по состоянию на конец марта 2005 г., средний возраст безработных в России составил 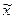= 34,4 года при среднем квадратическом отклонении σ = 13,8 года. С вероятностью p = 0,997 определить пределы, в которых находится средний возраст безработных в генеральной совокупности, если известно, что в ходе обследования опрошено п = 155 тыс. человек в возрасте 15—72 лет, что составляет 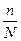= 0,15% от общей численности населения в этом возрасте.

Средняя ошибка выборки при собственно случайном бесповторном отборе составит:

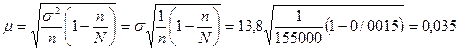года.

При 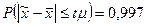коэффициент доверия t = 3 (см. Приложение 2), а предельная ошибка выборки

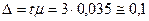года.

Таким образом, средний возраст безработных в России с вероятностью 0,997 находится в пределах

,

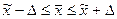т.е.

,

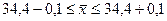или

.

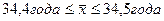При решении данной задачи среднюю ошибку выборки можно рассчитать по формуле для повторного отбора, поскольку величин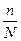а мала.

Пример. С вероятностью 0,954 определить предельную ошибку выборки для доли мужчин среди безработных в России в конце марта 1996 г., если известно, что в выборке (n = 155 тыс. человек) их доля составила 54,9%.

При 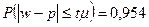коэффициент доверия t = 2(см. Приложение 1).

Предельная ошибка выборки

,

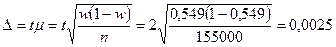т.е. Δ = 0,27%.

Следовательно, с вероятностью 0,954 можно утверждать, что в генеральной совокупности предельная ошибка выборки для доли безработных мужчин не превысит 0,25%.

Можно решить и обратную задачу: задав предельную ошибку выборки, определить вероятность, с которой она может быть гарантирована. При этом, зная Δ и µ, сначала находят коэффициент доверия t = Δ/ µ, а затем по таблице (см. Приложение 1) искомое значение вероятности.

3. Основные способы формирования выборочной совокупности

Рассмотренный в параграфе 2 собственно случайный способ формирования выборочной совокупности теоретически наиболее простой, но он предполагает, что в распоряжении исследователя имеется полный перечень единиц. На практике более широко используется механический отбор, основанный на предварительном упорядочении генеральной совокупности. Например, при проведении выборочных социально-демографических обследований составляются списки жилых помещений, при обследовании предприятий — их регистры и т.д. Устанавливается процент отбора, исходя из которого определяется число отбираемых единиц. Например, при формировании 5-процентной выборки из 1 млн единиц необходимо обследовать 50 тыс., т.е. из каждых 20 единиц одну. Затем определяется начало отбора, т.е. номер первой обследуемой единицы. Каждая следующая единица включается в выборку в соответствии с установленным шагом отбора. В приведенном примере из списка следует отбирать каждую 20-ю единицу.

Механический способ отбора часто используется на практике, так как он позволяет проводить оперативную замену одной единицы наблюдения на другую, стоящую в списке непосредственно перед или за единицей, первоначально включенной в выборку. Необходимость замены единиц наблюдения довольно часто возникает в связи с отказом респондентов от участия в обследовании или отсутствием их по соответствующему адресу. Например, при проведении выборочных бюджетных обследований населения в России ротация выборки, обусловленная указанной причиной, ежегодно составляет 15-20%.

Начало отсчета определяется разными способами. Если предварительное упорядочение единиц генеральной совокупности по какому-либо признаку не проводится, а список единиц (или регистр) составляется в порядке их поступления (например, регистр предприятий), то начало отсчета устанавливается в случайном порядке, а каждая следующая единица отбирается из списка через установленный интервал отсчета. Например, если началом отсчета при 5-процентном отборе является 20-я единица, то следующая — 40-я, затем 60-я и т.д.

При механическом отборе из совокупности, упорядоченной по какому-либо признаку, очень важно правильно выбрать начало отсчета. Например, при изучении бюджетов домашних хозяйств списки можно составлять в зависимости от заработной платы работников, поэтому выбор в качестве начала отсчета первой или последней единицы из каждой группы приведет к появлению ситематической ошибки выборки. Чтобы этого не происходило, необходимо из каждой группы отобрать единицу, которая находится в ее середине. При проведении выборочных социально-демографических обследований необходимо включить в выборку семьи разного состава. Поэтому из списка жилых помещений недостаточно механически отобрать каждое следующее в соответствии с установленным номером, требуется менять начало отсчета. Это позволяет исключить в выборке возможный перекос в сторону семей того или иного состава.

Если предварительное упорядочение проводится, то теоретически из общей ошибки выборки необходимо выделить ее случайную и систематическую компоненты. Однако практически это невозможно, поскольку в каждой группе обследуется одна единица. Поэтому при механическом отборе используются те же формулы для нахождения ошибки выборки, что и при собственно случайном отборе (табл. 3.1)

Таблица 3.1

Формулы средней ошибки выборки при собственно случайном и механическом отборе

Оцениваемый параметр	Повторный отбор	Бесповторный отбор
Средняя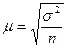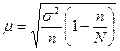
Доля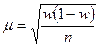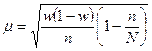

В последние годы более широкое практическое применение получил типический (стратифицированный, расслоенный) отбор, при котором обследуемая совокупность предварительно разбивается на типически однородные группы и выбор осуществляется из каждой такой группы механическим или собственно случайным способом.

Типический способ отбора используется в нашей стране при проведении выборочных бюджетных обследований домашних хозяйств, изучении потребительских ожиданий населения, при организации выборочных обследований по проблемам занятости, анализе результатов деятельности малых предприятий и их деловой активности.

До 1996 г. при формировании выборочной совокупности домашних хозяйств для проведения бюджетных обследований применялась типическая выборка с механическим отбором единиц внутри групп. На первом этапе отбора в качестве типических групп использовалась территориально-отраслевая группировка рабочих и служащих, а на втором — группировка по средней месячной оплате труда. В настоящее время при проведении таких обследований применяется более сложная процедура отбора, также основанная на выделении типически однородных, групп.

При проведении ежеквартальных выборочных обследований малых предприятий используется многомерная типическая выборка, объем которой составляет примерно 20% от общей численности таких предприятий. Расслоение объектов генеральной совокупности по типически однородным группам проводится в соответствии со следующими признаками: территория, отрасль, форма собственности, выручка от реализации продукции (работ, услуг).

Из каждой выделенной группы при проведении типического отбора в выборочную совокупность отбирается определенное число единиц. Обозначим число единиц, попавших в выборку из i-й группы, через ni а общее число образованных групп через m (i= 1, 2,…m). Величину ni можно задать одним из трех способов:

• отбор из каждой группы равного числа единиц, т.е.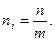

Использование такого принципа отбора позволяет получить достаточно надежные результаты лишь при равных размерах выделенных типических групп. Если же их численность существенно различается между собой, то использование равномерного отбора может привести к смещению оценок, полученных по результатам выборочного обследования;

• отбор единиц пропорционально их численности в соответствующих группах генеральной совокупности, т.е. 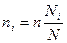, где Ni – число единиц в i-й типической группе генеральной совокупности. Использование этого принципа формирования выборочной совокупности обеспечивает достаточно надежные результаты, если колеблемость признака несущественно различается в разных группах генеральной совокупности. Если же коэффициенты вариации в них различаются существенно, то репрезентативность выборки при таком способе ее формирования может оказаться невысокой;

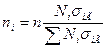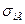• оптимальное размещение, учитывающее не только численность групп, но и степень вариации в них изучаемого признака, т.е. , где – среднее квадратическое отклонение признака в i-й группе генеральной совокупности. Данная формула получена следующим образом:

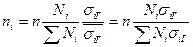, (3.1)

где 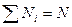, а 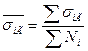– средняя из групповых средних квадратических отклонений.

Оптимальное размещение позволяет минимизировать среднюю ошибку выборки. Впервые ответ на вопрос о наиболее эффективной организации типической (расслоенной) выборки был получен в 1920 г. А.А. Чупровым и независимо от него в 1934 г. Е. Нейманом. В статистике такое размещение называется также неймановым. Хотя оно позволяет получить более точные результаты, на практике осуществить его сложно, поскольку необходимо знать вариацию признака в генеральной совокупности еще до проведения обследования.

В статистической практике нашей страны пропорциональный способ отбора используется при формировании выборочной совокупности для проведения наблюдения за деловой активностью малых предприятий в промышленности.

Для ежеквартального наблюдения за основными экономическими показателями, характеризующими деятельность малых предприятий, выборка строится с использованием принципа оптимального размещения.

Опыт практического применения принципа оптимального размещения показал, что использование в качестве показателя вариации в формуле (3.1) среднего квадратического отклонения по i-й типической группе генеральной совокупности позволяет обеспечить оптимальное размещение единиц выборочной совокупности по типическим группам лишь в том случае, если нет существенных различий в значениях коэффициентов вариации по этим группам. При проведении выборочного обследования всех предприятий региона, а не только малых, высокое значение среднего квадратического отклонения может иметь место при низком значении коэффициента вариации (например, на крупных предприятиях) и наоборот. В результате крайне неоднородные группы объектов, например малые предприятия, будут недостаточно представлены в выборке. В таком случае в формуле (3.1) целесообразно использовать не среднее квадратическое отклонение, а коэффициент вариации.

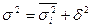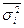Общая дисперсия изучаемого признака, согласно правилу сложения дисперсий, может быть представлена как сумма , где — средняя из групповых дисперсий, а 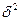— межгрупповая дисперсия. При проведении типического отбора межгрупповая дисперсия не носит характера случайной вариации, так как группы образованы еще до начала выборочного обследования. Следовательно, при нахождении ошибки выборки необходимо из двух указанных слагаемых обшей дисперсии учесть лишь то, которое связано со случайной вариацией, а именно среднюю из групповых дисперсий в выборке .

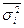При отборе пропорционально численности групп средняя из групповых дисперсий 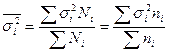. В этом случае средняя ошибка выборки при бесповторном отборе:

для средней

,

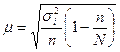для доли

,

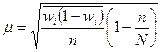где w_i – доля единиц совокупности, обладающих изучаемым признаком в i -й типической группе;

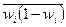- средняя из групповых дисперсий для доли.

В таблице 3.2 представлены формулы для исчисления средней ошибки выборки при типическом отборе.

Таблица 3.2

Формулы средней ошибки выборки при типическом отборе

Оцениваемый параметр	Повторный отбор	Бесповторный отбор
Пропорциональное распределение единиц выборочной совокупности по группам
Средняя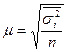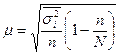
Доля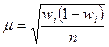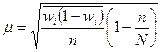
Оптимальное распределение единиц выборочной совокупности по группам
Средняя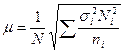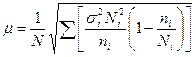
Доля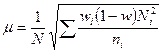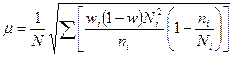

Разновидностью типической является районированная выборка, при которой отбор единиц для наблюдения проводится из групп, представленных административно-территориальными образованиями. В этом случае преимущества типической выборки проявляются лишь при заметном расхождении среднего значения изучаемого по отдельным регионам.

Применение типического отбора позволяет уменьшить среднюю ошибку выборки, но его преимущества проявляются только при условии, что различия в средних значениях изучаемого признака между группами достаточно ощутимы, а вариация признака внутри каждой группы невелика.

Если при построении типической выборки предполагается получить значение нескольких показателей, то расслоение проводится, как правило, не по наблюдаемым, а по вспомогательному признаку. При этом вспомогательный признак должен коррелировать с наблюдаемыми. Например, численность домашних хозяйств определенного типа (одиночки; семьи, состоящие из двоих взрослых; семьи с разным числом детей) коррелирует с показателями доходов и расходов.

Пример. Для изучения объема и структуры доходов работников городских торговых предприятий, относящихся к разным формам собственности, проведен 2-процентный бесповторный типический отбор, результаты которого по одному из обследованных показателей приведены в табл. 3.3.

Таблица 3.3

Форма собственности	Числен-ность занятых, чел. Ni	Обсле-довано человек ni	Доход от участия в собственности предприятия на одного работника в год,тыс. руб.
средний xi	среднее квадратическое отклонение σi
Государственная
Негосударст- венная
Всего

В данном случае отбор проведен пропорционально численности работников, занятых на предприятиях каждой выделенной группы. Для того чтобы найти пределы, в которых указанный вид дохода работников торговли находится в генеральной совокупности, зададим доверительную вероятность Р = 0,95. Следовательно, коэффициент доверия t = 1,96 (см. Приложение 1).

В выборочной совокупности средняя сумма дохода от участия в собственности предприятия

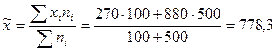тыс. руб.

Для нахождения средней ошибки выборки необходимо знать среднюю из групповых дисперсий:

.

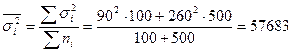Предельная ошибка выборки

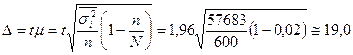тыс. руб

Следовательно, с вероятностью 0,95 можно сделать вывод о том, что среди торговых работников города средний годовой доход от участия в собственности предприятия находится в пределах

,

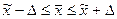т.е

,

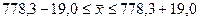или

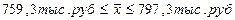
Для того чтобы на основе приведенных данных сформировать выборочную совокупность с учетом не только численности выделенных групп в генеральной совокупности, но и степени вариации в них изучаемого признака, надо исходить из предположения, что групповые дисперсии в выборочной и генеральной совокупности равны, т.е. 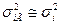. Общий объем выборки n = 600 чел. с учетом степени вариации признака по формам собственности должен быть распределен следующим образом:

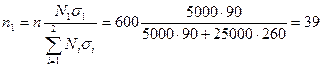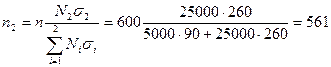чел.;

чел.

Таким образом, при оптимальном размещении необходимо обследовать 39 работников государственных торговых предприятий и 561 — негосударственных. В этом случае средняя ошибка выборки

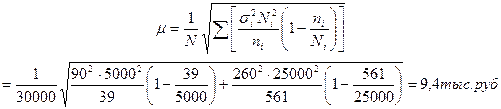
При Р= 0,95 предельная ошибка выборки равна 18,4 тыс. руб., т.е. немного меньше, чем при пропорциональном отборе.

Серийный (гнездовой) отбор применяется в том случае, если генеральная совокупность разбита на группы еще до начала выборочного обследования. При проведении выборки исследователь может из генеральной совокупности отбирать не отдельные единицы, а целые их серии и обследовать в рамках каждой серии все попавшие в нее единицы. Такой способ отбора широко применяется при контроле качества продукции, когда для проведения наблюдения вскрывается упаковка, содержащая определенное количество изделий, и все они проверяются. Если бы в этом случае из каждой упаковки обследовалась лишь одна единица, потребовалось бы повторно упаковывать всю партию товара, что привело бы к дополнительному увеличению затрат, связанных с обследованием.

Исследователь отбирает из генеральной совокупности в случайном порядке более крупные единицы (серии), поэтому возникновение случайной ошибки связано с отклонением серийных средних от общей средней. Поскольку внутри отобранных серий обследуются все единицы, то вариация признака в рамках каждой серии носит характер не случайной, а систематической составляющей и, следовательно, не должна учитываться при расчете средней ошибки выборки. Таким образом, в формуле средней ошибки выборки вместо общей дисперсии необходимо использовать межсерийную дисперсию.

Обозначим число серий в генеральной совокупности через S, а в выборке — через s.

Межсерийная дисперсия при равновеликих сериях рассчитывается по формуле

,

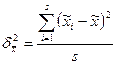где 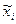- среднее значение признака в i-й серии;

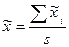- общая средняя в выборочной совокупности.

При бесповторном серийном отборе средняя ошибка выборки

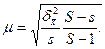
Если число серий в генеральной совокупности велико, то вместо (S- 1) в последней формуле можно использовать величину S. В знаменателе первой дроби величина s берется лишь при большом объеме выборки (s > 30). Если число отобранных серий невелико, вместо s должна быть величина (s - 1).

При нахождении межсерийной дисперсии для доли необходимо учесть, что среднее значение альтернативного признака равно р, т.е. доле единиц, обладающих этим признаком. Соответственно, оно будет равно w в выборке и w_i в каждой отобранной серии. В таком случае межсерийная дисперсия для доли

.

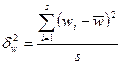При равновеликих сериях .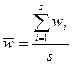

При серийном отборе средняя ошибка выборки рассчитывается по формулам, приведенным в табл. 3.4.

При рассмотренных способах формирования выборочной совокупности отбор единиц для наблюдения осуществляется уже на первом этапе. Такой отбор называется одноступенчатым. Однако на практике часто используется многоступенчатый отбор, при котором на первом этапе из совокупности отбираются укрупненные единицы (серии), а затем без проведения наблюдения за всеми единицами в рамках серии осуществляется собственно случайный или механический отбор единиц из каждой отобранной серии.

Таблица 3.4

Формулы средней ошибки выборки при серийном отборе

Оцениваемый параметр	Повторный отбор*	Бесповторный отбор
Средняя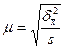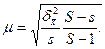
Доля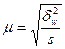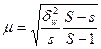

* При серийной выборке повторный отбор практически не применим, поэтому в основном используются формулы ошибок для бесповторного отбора.

Ошибка выборки при двухступенчатом отборе складывается из ошибок, возникающих на каждой ступени. В данном случае

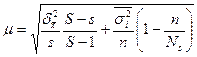, (3.2)

где 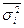- средняя из серийных дисперсий;

N_S– общее число единиц совокупности в отобранных сериях.

При построении многоступенчатой выборки используется комбинация разных способов отбора, поэтому такой способ отбора иногда называют комбинированной выборкой.

От многоступенчатого следует отличать многофазный отбор, при котором из единиц совокупности, отобранных на первом этапе, осуществляется подвыборка в целях изучения дополнительных характеристик обследуемой совокупности. При многофазном отборе единица отбора на каждом этапе одна и та же, а при многоступенчатом она меняется: на первой ступени отбираются единицы более высокого порядка (например, серии), чем на второй. Многофазная выборка используется для расширения программы обследования. На второй фазе целесообразно изучать такие признаки, которые обладают меньшей вариацией в генеральной совокупности. Это позволяет сэкономить средства, необходимые для выборочного обследования. Отметим, что на каждой фазе многофазных выборок рассчитывается особое значение ошибки выборки.

Взаимопроникающие выборки — форма выборочного обследования, при которой из одной генеральной совокупности одним и тем же способом формируются две (или более) выборочные совокупности. При этом происходит взаимное уточнение результатов обследования.

Выборочные обследования широко применяются в отечественной статистической практике. Этот метод используется, например, при организации специальных статистических обследований, изучении общественного мнения и т.д.

4. Определение необходимой численности выборки

При разработке программы выборочного обследования одним из наиболее сложных является вопрос о том, сколько единиц изучаемой совокупности необходимо обследовать, т.е. об объеме выборки. В параграфах 2 и 3 показано, что при любом способе отбора предельная ошибка выборки обратно пропорциональна числу обследованных единиц. Чтобы уменьшить ошибку выборки, необходимо увеличить ее объем, но при этом возрастут и затраты на проведение обследования. Определяя необходимую численность выборочной совокупности, приходится прежде всего оценивать допустимую ошибку.

Как определить необходимую численность выборки при собственно случайном или механическом повторном отборе? В этом случае предельная ошибка выборки для средней

,

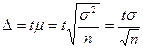а необходимая ее численность

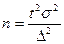. (4.1)

Для определения необходимой численности выборки должны быть заданы предельная ее ошибка и вероятность того, что эта ошибка не превысит заданного предела. В соответствии с этой вероятностью по таблице Приложения 1 находят коэффициент доверия t.

Наиболее сложно определить дисперсию изучаемого признака в генеральной совокупности. До проведения обследования приближенно оценить дисперсию или среднее квадратическое отклонение можно на следующей основе:

· исходя из результатов специально организованного пробного обследования;

опираясь на данные предыдущих обследований, как выборочных, так и сплошных. В последние годы в статистической практике все чаще вместо сплошного наблюдения применяют выборочный метод. Например, с 1996 г. проводят выборочное наблюдение за деятельностью малых предприятий. Таким образом, дисперсию изучаемого признака в выборке можно оценить, зная коэффициент вариации, значение которого получено по итогам предшествующего сплошного наблюдения или предшествующей выборки. Коэффициент вариации 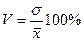. Следовательно, дисперсия ;

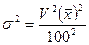· исходя из закона распределения изучаемого признака в генеральной совокупности.

Если распределение близко к нормальному, то размах вариации R в 6 раз больше среднего квадратического отклонения: R = 6σ, где R = xmax — xmin. В таком случае, зная максимальное и минимальное значения признака, можно оценить σ:

.

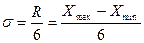Если в результате выборочного обследования необходимо установить долю единиц, обладающих определенным значением альтернативного признака, то дисперсия для доли будет равна pq, В этом случае формула необходимой численности выборки примет вид

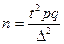. (4.2)

Максимальное значение дисперсии альтернативного признака равно 0,25, т.е. max (pq) = 0,25 (при р = q = 0,5). Если доля единиц, обладающих изучаемым признаком, т.е. р, неизвестна, в расчете необходимой численности выборки можно использовать указанное максимальное значение для дисперсии альтернативного признака.

На практике величина допустимой ошибки выборки, как правило, устанавливается не в абсолютном, а в относительном выражении: 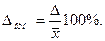Так как 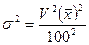, формулу для определения необходимой численности выборки при собственно случайном или механическом повторном отборе можно представить следующим образом:

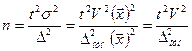. (4.3)

Пример. Для изучения товарооборота по выделенной товарной группе планируется провести выборочное обследование торговых предприятий региона. Сколько предприятий розничной торговли необходимо обследовать, если по данным предшествующего обследования известно, что коэффициент вариации товарооборота по данной группе товаров составляет 90%, а предельная относительная ошибка выборки с вероятностью 0,95 не должна превысить 5%?

При Р = 0,95 коэффициент доверия t = 1,96 (см. Приложение 1). Следовательно, 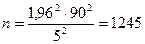, т.е. при повторном отборе необходимо обследовать 1245 торговых предприятий.

Рассмотрим формулы для нахождения необходимой численности выборки при бесповторном отборе.

Предельная ошибка выборки при собственно случайном или механическом бесповторном отборе рассчитывается по формуле 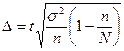, поэтому необходимая для достижения заданной ошибки численность выборки

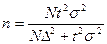. (4.4)

Если задана предельная относительная ошибка выборки и известен коэффициент вариации, то численность выборки определяется по формуле

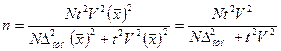(4.5)

При бесповторном отборе для нахождения доли альтернативного признака необходимая численность выборки