Фундаментальна група

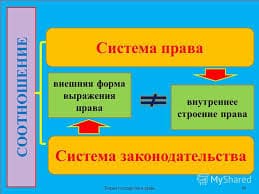
1. Шляхи і петлі. Частинка, яка рухається в просторі протягом якогось часу, описує деякий шлях. Для зручності припустимо, що рух починається у момент часу t=0 і продовжується до часу зупинки, який може бути різним для різних шляхів, але обов’язково є додатнім або ж рівним нулю. Для двох дійсних чисел х і у, х ≤ у, позначимо [x, y] множину всіх дійсних чисел t, які задовольняють нерівність x ≤ t ≤ y. Шлях а в топологічному просторі Х є неперервним відображенням

а: [0, | | а ||] -– > X.

Число || а || позначає тут час зупинки. Припускаємо, що || а || ≥ 0. Точки а (0) і а (|| а ||) в просторі Х є початковою і кінцевою точками шляху а відповідно.

Необхідно відрізняти шлях s від множини точок а (t) простору Х, коли t пробігає відрізок [0, || а ||]. Різні шляхи можуть мати однакові точкові образи. Нехай, наприклад, Х – одиничне коло на площині, яке задане в полярних координатах (r, θ) рівнянням r = 1. Два наступних шляхи

а (t) = (1, t), 0 ≤ t ≤ 2π,

b (t) = (1, 2t), 0 ≤ t ≤ 2π,

є різними, не дивлячись на те, що у них однаковий час зупинки, однакові точки початку і кінця і однаковий точковий образ. Два шляхи а і b рівні тоді і тільки тоді, коли вони мають однакову область визначення, тобто || а || = ||b||, і якщо при кожному t з цієї області а (t) = b (t).

Розглянемо тепер два таких шляхи а і b в Х, що початкова точка шляху b співпадає з кінцем шляху а, тобто а (|| а ||) = b (0). Добуток а · b шляхів а і b визначається формулою

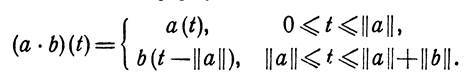
Ця формула визначає неперервне відображення, а · b це шлях в Х. Його час зупинки

||а · b||= ||а|| + ||b||.

Звернемо увагу на те, що добуток двох шляхів визначений тільки тоді, коли кінцева точка першого шляху співпадає з початковою точкою другого.

Очевидно, що наступні три твердження:

(І) добутки а · b і b · с визначені,

(ІІ) добуток а · (b · с) визначений,

(ІІІ) добуток (а · b) · с визначений,

еквівалентні і що при виконанні цих умов має місце асоціативний закон

а · (b · с) = (а · b) · с.

шлях а називається одиничним шляхом або одиницею, якщо він має час зупинки ||а|| = 0. Ця термінологія відображає той факт, що множина всіх одиничних шляхів у деякому топологічному просторі може бути охарактеризована як множина всіх одиниць відносно введеного вище множення. Це означає, що шлях е є одиницею тоді і тільки тоді, коли е · а = а і b · е = b кожен раз, коли ці добутки визначені. Очевидно, що образом одиничного шляху є точка, і, навпаки, існує єдиний одиничний шлях, образом якого є будь-яка точка простору. Шлях, образ якого складається з однієї точки, називається постійним шляхом. Кожен одиничний шлях є постійним, але не навпаки.

Для довільного шляху а позначимо через а^{- 1} обернений шлях, утворений проходженням шляху а протилежному напрямі. Це означає, що

а^{- 1} (t) = а ( || а || - t), 0 ≤ t ≤ || а ||.

Сенс цієї назви і позначення для шляху а^{- 1} стане зрозумілим трохи згодом. Зрозуміло, що шлях а · а^{- 1} є одиницею лиш тоді, коли а = е.

Алгебрагічна структура введена вище ще досить далека від структури групи. Один з методів вдосконалення цієї ситуації полягає в тому, щоб вибрати довільну точку р в Х і обмежитися розглядом шляхів, які починаються і закінчуються в цій точці. Шлях, у якого початкова і кінцева точки співпадають, називається петлею, а його єдина кінцева точка – базисною точкою. Петля з базисною точкою р надалі буде часто називатись р -базисною. Є визначеним добуток двох р -базисних петель і він є р -базисним. Одиничний шлях, який відповідає точці р, є мультиплікативною одиницею. Аналізуючи ці примітки, отримуємо, що множина всіх р -базисних петель простору Х утворює напівтрупу з одиницею.

2. Класи шляхів і петель. Набір шляхів h_s, 0 ≤ s ≤ 1, простору Х називається неперервним сімейством шляхів, якщо

(І) час зупинки ||h_s|| неперервно залежить від s;

(ІІ) функція h, визначена формулою h (s, t) = h_s (t), неперервно відображає замкнену область 0 ≤ s ≤ 1, 0 ≤ t ≤ ||h_s|| в простір Х.

Необхідно звернути увагу на те, що функція двох змінних, неперервна в кожній точці своєї області визначення по кожній змінній, не обов’язково неперервна на сукупності змінних. Функція f, визначена на одиничному квадраті 0 ≤ s ≤ 1, 0 ≤ t ≤ 1 формулою

1, якщо s = t = 0,

f(s, t) =

s + t в інших випадках,

s² +t²

дає нам приклад такого роду. Тому сімейство шляхів {f_s}, визначене рівністю f_s (t) = f (s, t), не є неперервним сімейством.

Сімейство шляхів з фіксованими кінцями – це таке неперервне сімейство {h_s}, 0 ≤ s ≤ 1, що точки h_s(0) і h_s (||h_s||) не залежить від s, тобто існують такі точки p і q простору Х, що h_s(0) = р і h_s (||h_s||) = q для всіх s з відрізку [0, 1].

Нехай а і b – два шляхи в топологічному просторі Х. Шлях а називається еквівалентним шляху b (а ~ b), якщо існує таке сімейство шляхів {h_s}, 0 ≤ s ≤ 1, з фіксованими кінцями, що а = h₀, b = h₁ .

Відношення ~ рефлексивне, тобто для будь-якого шляху маємо а ~ а, так як ми можемо, очевидно, покласти h_s(t) = а (t), 0 ≤ s ≤ 1. Це відношення також симетричне, тобто з а ~ b слідує, що b ~ а, так як можна покласти k_s(t) = h_1-s (t). Крім того, це відношення є транзитивним, тобто з а ~ b і b ~ с слідує, що а ~ с. Для перевірки останнього твердження, припустимо, що h_s і k_s – сімейства з фіксованими кінцями, які реалізують еквівалентності а ~ b і b ~ с відповідно. Тоді набір шляхів {j_s}, який визначений рівністю

h_2s(t), 0 ≤ s ≤ ½,

j_s (t) =

k_2s-1 (t), ½ ≤ s ≤ 1,

і є сімейством шляхів з фіксованими кінцями, які показують, що а ~ с.

Отже, відношення ~ є справжнім відношенням еквівалентності, тому множина всіх шляхів простору Х розбивається на класи еквівалентності. Клас еквівалентності, що містить шлях а, позначимо через [ а ]. Це значить, що клас [ а ] складається із всіх шляхів b таких, що а ~ b. Маємо рівність [ а ]=[ b ] тоді і тільки тоді, коли а ~ b. Сукупність всіх класів еквівалентності шляхів топологічного простору Х позначимо як Г(Х). Це фундаментальний групоїд простору Х.

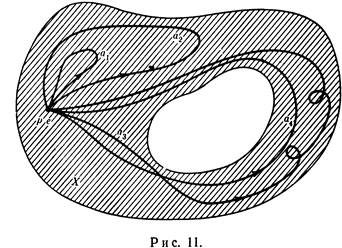
З геометричної точки зору шляхи а і b еквівалентні тоді і тільки тоді, коли один з них можна неперервно деформувати в інший в просторі Х, не рухаючи кінцеві точки. Нехай, наприклад, Х – кільцева область зображена на рис. 11. Розглянемо п’ять петель: е (одиниця), а ₁, а ₂, а ₃, а ₄ на Х з базисною точкою р. Маємо серед них наступні еквівалентності:

а ₁ ~ а ₂ ~ е,

а ₃ ~ а ₄.

Але не вірно, що

а ₁ ~ а _3.

Рис. 11 показує, що деякі важливі властивості простору Х відображаються структурою класів еквівалентності петель.

Якщо, наприклад, точки області, обмеженої внутрішньою граничною лінією кільця Х, включити в склад простору Х, тобто заклеїти дірку, то всі петлі з базисною точкою р стануть еквівалентними е. Мається на увазі, що стрілки на рис. 11 вказують, яким чином параметр t пробігає шлях а _i. Образ точки t пробігає цикл а _i один раз в напрямі, вказаному стрілкою. Цим підкреслюється ідея того, що а _i – функція. Сукупність точок, які складають шлях, не визначають шлях повністю; наприклад, а ₃ = а ₃ · а ₃, більш того, невірно, що а ₃ ~ а ₃ · а _3.

Покажемо, що множення шляхів індукує множення в фундаментальному групоїді Г(х). У результаті ми зможемо перенести нашу увагу з шляхів і операцій їх перемноження на класи еквівалентності і операцію множення цих класів.

Зробивши це, ми отримаємо необхідну алгебрагічну структуру для визначення фундаментальної групи.

(2.1) Нехай а, а ´, b, b ´ - деякі шляхи в Х. Якщо добуток а · b визначений і

а ~ а ´, b ~ b ´ ,то добуток а ´ · b ´ також визначений і а · b ~ а ´ · b ´.

Доведення. Якщо {h_s} і {k_s} – сімейства шляхів з фіксованими кінцями, яке здійснює еквівалентності а ~ а ´ і b ~ b ´ відповідно, тоді сімейство шляхів {h_s · k_s} є сімейством шляхів з фіксованими кінцями, яке здійснює еквівалентність а · b ~ а ´ · b ´. Помітно, що добуток h_s · k_s визначені для всіх 0 ≤ s ≤ 1, так як

h_s (||h_s||) = h₀ (||h₀||) = а (|| а||) = b (0) = k₀ (0) = k_s (0).

Добуток а ´ · b ´ = h₁ · k₁ визначений. Можна перевірити, що функція h · k, визначена рівністю

(h · k) (s, t) = (h_s · k_s) (t), 0 ≤ s ≤ 1, 0 ≤ t ≤ | | h_s||+ ||k_s||

неперервна на сукупності змінних s і t. Так як величина ||h_s · k_s|| = ||h_s|| + ||k_s|| неперервно залежить від s, шляхи h_s · k_s утворюють неперервне сімейство. Далі маємо

(h_s · k_s) (0) = h_s (0) = а (0)

і

(h_s · k_s) (||h_s · k_s||) = k_s(||k_s||) = b (|| b ||),

так що {h_s · k_s}, 0 ≤ s ≤ 1, є сімейством з фіксованими кінцями. Але оскільки h₀ · k₀ = а · b і h₁ · k₁ = а ´ · b ´, то доведення завершене.

Розглянемо тепер два таких шляхи а і b в просторі Х, що добуток

а · b є визначеним. Тоді добуток класів еквівалентності [ а ]і[ b ] визначається формулою [ а ] · [ b ] = [ а · b ]. Попередньо доведена теорема показує, що множення в Г(Х) коректне.

Так як всі шляхи, які належать одному класу еквівалентності, мають одні і ті ж кінцеві точки, ми можемо визначити початкову і кінцеву точки будь-якого елемента а є Г(Х) як відповідні точки довільного шляху, який представляє клас α. Добуток α · β двох елементів з Г(Х) визначений, якщо кінцева точка елемента α співпадає з початковою точкою елемента β. Оскільки відображення а -– > [ а ] зберігає множення, асоціативний закон має місце і в Г(Х) завжди, коли відповідні шляхи визначені точно так, як і для шляхів.

Елемент ε з Г(Х) називається одиницею, якщо він містить одиничний шлях. Як і вище, маємо: елемент ε є одиницею, якщо ε · α = α і β · ε = β кожен раз, коли добутки ε · α і β · ε визначені. Це твердження майже очевидне з відповідного твердження для шляхів. Саме шлях ε – одиниця. Припустимо, що добуток ε · α визначений. Нехай е – одиничний шлях з класу ε і а – шлях з класу α. Аналогічно отримаємо, що β · ε = β. Навпаки, припустимо, що ε – не одиниця. Для доведення існування такого класу α, що добуток ε · α визначено і ε · α = α, візьмемо в якості представника класу α одиничний шлях, який відповідає кінцевій точці елемента ε. Тоді добуток

ε · α визначений і, так як α – одиниця, ε · α = ε. Отже, якщо ε · α = α, клас ε є одиницею, що суперечить нашому припущенню. Це завершує доведення. Звернемо увагу на те, що групоїд Г(Х) має таку ж структуру, як і множина шляхів в Х. Цікаво тут те, що насправді структура в Г(Х) є значно багатшою.

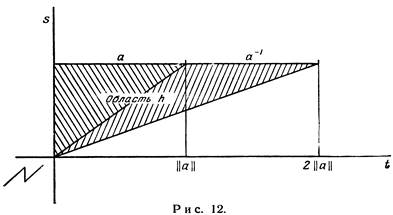
(2. 2) Для будь-якого а в Х існують такі одиничні шляхи е ₁ і е ₂, що а · а^-1 ~ е ₁, а^-1 · а= е _2.

Доведення. Шляхи е ₁ і е ₂, очевидно, є одиницями, які відповідають початковій і кінцевій точкам шляху а. Розглянемо сімейство шляхів {h_s}, 0 ≤ s ≤ 1, визначене формулою

а (t), 0 ≤ t ≤ s|| а||,

h_s(t) =

а (2|| а || - t), s|| а|| ≤ t ≤ 2 s|| а||.

Область визначення відображення h, визначеного рівністю h (s, t) = h_s (t), заштрихована на рис. 12. На прямій t = 0, тобто на s-осі, відображення h тотожньо рівне а (0). Теж саме виконується для прямої t = 2 s|| а||. Отже, шляхи h_s утворюють сімейство з фіксованими кінцями.

По змінній t вздовж горизонталі s = 1 функція h поводить себе так само, як і функція а · а^-1. Маємо

h₀ = e ₁,

а (t), 0 ≤ t ≤ || а||,

h₁(t) =

а (2|| а || - t), || а|| ≤ t ≤ 2 || а||,

звідки

а (t), 0 ≤ t ≤ || а||,

h₁(t) =

а ^-1(t - || а ||), || а|| ≤ t ≤ 2 || а||,

= а · а^-1 (t).

Це і показує, що а · а^-1 ~ е_1. Друга еквівалентність із (2.2) може бути доведена аналогічно; але простіше використати вже отриманий результат. Візьмемо, що а · (а^-1)^-1 ~ е_2. Але так як (а^-1)^-1 = а, то наше твердження доведене.

(2.3) Якщо два шляхи а і b такі, що а ~ b, то а^-1 ~ b^-1.

Доведення. Дане твердження випливає з (2.1) і (2.2). А саме

а^-1 ~ а^-1 · b· b^-1 ~ а^-1 а · b^-1 ~ b^-1.

Спираючись на (2.3), можемо для довільного елемента α з Г(Х) визначити обернений формулою

α^-1 = [ а^-1 ], де а - довільний шлях з α.

Елемент α^-1 залежить від α і не залежить від вибору представника а, тобто клас α^-1 визначений коректно. Сенс цього позначення твердження (2.4), яке є наслідком (2.2).

(2.4) Для будь-якого елемента α з Г(Х) знайдуться такі одиниці ε₁ і ε₂, що α · α^{-1 =} ε₁ і α^-1 · α = ε_2.

Це твердження виражає властивість фундаментального групоїда Г(Х), яка відрізняє його від множини всіх шляхів простору Х. Тепер можна визначити фундаментальну групу простру Х з базисною точкою р, відношення а -– > [ а ] визначає відображення напівтрупи всіх р -базисних петель на π (Х, р), яке зберігає множення; відповідно, π (Х, р) – напівгрупа з одиницею, і в силу (2.4) маємо

(2.5) Множина π(Х, р) разом з введеним вище множенням утворює групу, яка за означенням називається фундаментальною групою простору Х з базисною точкою р.

(2.6) Будь-який постійний шлях еквівалентний деякому одиничному шляху.

Доведення. Нехай k – деякий постійний шлях в Х, визначений рівністю

k(t) = p, 0 ≤ t ≤ ||k ||,

де р – деяка точка з простору Х. Очевидно, що набір шляхів, який визначений рівністю

h_s (t) = р, 0 ≤ t ≤ s||k ||,

є сімейством з фіксованими кінцями, h₁ = k і h₀ = е, де е – одиничний шлях, яки відповідає точці р.

3. Зміна базисної точки. Фундаментальна група π(Х, р) простору Х визначена відносно базисної точки р і залежить від її вибору. Але зараз ми побачимо, що якщо простір Х лінійно зв’язний, то всі його фундаментальні групи, які відповідають різним базисним точкам, ізоморфні між собою. Топологічний простір Х називається лінійно зв’язним, якщо його дві довільні точки можна з’єднати шляхом з Х.

(3.1) Нехай α – деякий елемент групоїда Г(Х) з початковою точкою р і кінцевою р ´. Тоді відношення

β α^-1 · β · α, де β пробігає групу π(Х, р)

здійснює ізоморфізм між групами π(Х, р) і π(Х, р´).

Доведення. Добуток α^-1 · β · α, звичайно, визначено, і зрозуміло, що α^-1 · β · α є π(Х, р´). Для довільних елементів β₁, β₂ α є π(Х, р) маємо

β₁ · β₂ α^-1 · (β₁ · β₂) · α = (α^-1 · β₁ · α) · (α^-1 · β₂ · α),

так що ця відповідність є гомеоморфізмом. Припустимо далі, що α^-1 · β · α = =1 (=ε). Тоді

β = α · α^-1 · β · α · α^-1 = α · α^-1 = 1,

звідси можна сказати, що ця відповідність – ізоморфізм. Для будь-якого елемента γ групи π(Х, р´) елемент α^-1 · γ · α лежить в π(Х, р), і, очевидно, що

α^-1 · γ · α γ.

Таким чином, це відображення є відображенням на і доведення завершено.

Наслідком (3.1) є те, що фундаментальна група лінійно зв’язного простору не залежить від базисної точки в тому сенсі, що групи, визначені в двох різних базисних точках є ізоморфні.

4. Індуковані гомоморфізми фундаментальної групи. Нехай існує деяке неперервне відображення f: Х Y топологічного простору Х в Y. Довільний шлях а простору Х визначає шлях f а в просторі Y, який задається композицією відображень

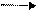
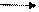[0, || a ||] ^a X ^f Y,

тобто fa (t) = f (a (t)). Час зупинки шляху fa,
очевидно, той же, що у шляху а, тобто ||fa|| = ||a||. Більше того, співвідношення а fa зберігає множення:

(4.1) Якщо добуток а · b визначений, то також визначений добуток fa · fb і f (a · b) = fa · fb.

Доведення цього э досить складним. Так як добуток a · b визначений, то a(||a||) = b(0). Відповідно,

fa(||fa||) = fa(||a||) = f(a||a||) = f(b(0)) = fb(0),

тобто добуток fa · fb визначений. Більше того,

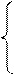f(a · b) (t) = f((a · b) (t)) =

f(a(t)), 0 ≤ t ≤ ||a||,

=

f(b(t - ||a||)), ||a|| ≤ t ≤ ||a|| + ||b||,

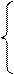
fa(t), 0 ≤ t ≤ ||fa||,

=

b(t - |f|a||)), ||fa|| ≤ t ≤ ||fa|| + ||fb||,

= (fa ·fb) (t).

Очевидно, що

(4.2) Якщо е – одиниця, то fe – теж одиниця. Більше того,

(4.3) fa^-1 = (fa)^-1.

Доведення.

fa^-1(t) = f(a^-1(t)) = f(a||a|| - t) = fa (||fa|| - t) = (fa)^-1 (t).

Для будь-якого неперервного відображення шляхів {h_s}, 0 ≤ s ≤ 1, в Х сімейство шляхів {fh_s} також буде неперервним. Більше того, сімейство {fh_s} має фіксовані кінці, якщо цю властивість має сімейство {h_s}. Відповідно,

(4.4) Якщо а ~ b, то fа ~ fb.

З вище сказаного слідує, що відображення f визначає відображення f_*

фундаментального групоїда Г(Y), яке задається формулою

f_* ([ a ]) = [ fa ].

Сумуємо основні властивості відображення f_*.

(4.5) (I) Якщо ε – одиниця, то f_*ε – теж одиниця.

(ІІ) Якщо добуток α · β визначений, то також визначений добуток f_*α · f_*β і f_* (α · β) = f_*α · f_*β.

(III) Якщо f: Х Х – тотожнє відображення, тобто f(x) = x, то f_* - також тотожнє відображення, тобто f_* (α) = α.

(IV) Якщо Х ^f Y ^g Z – неперервне выдображення і gf: Х Z – композиція, то (gf)_* = g_* · f_*.

Доведення цих тверджень випливає з (4.1), (4.2) і асоціативності композиції відображень, тобто (gf)a = g(fa).

Зрозуміло, що при довільному виборі базисної точки р в просторі Х f_* (π(Х, р)) ⊂ π(Y, fр). Отже, обмеження відображення f_* на групу π(Х, р) (яке позначимо так само через f_* )визначає гомоморфізм

f_* : π(Х, р) π(Y, f р),

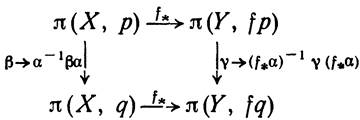який називається гомоморфізмом, індукованим відображенням f. Відзначимо, що, якщо простір Х лінійно зв’язний, алгебрагічні властивості гомоморфізму f_* не залежать від вибору базисної точки. Точніше, виберемо для двох довільних точок p, q є Х елемент α є Г(Х) з початковою точкою р і кінцевою q. Тоді гомоморфізми

(4.6)

утворюють комутативну діаграму, в якій вертикальні відображення є ізоморфізмамии на. В наслідок, якщо один з двох гомоморфізмів f_* є абогомоморфізмом на, або ізоморфізмом в, то таким є і другий.

Поняття гомоморфізму, індукованого неперервним відображенням, є фундаментальним в алгебрагічній топології. Гомоморфізм фундаментальної групи, індукований неперервним відображенням, є мостом від топології до алгебри в теорії вузлів. Наступна важлива теорема показує, як топологічні властивості відображення f відображаються на гомоморфізмі f_*.

(4.7) Теорема. Якщо відображення f: Х Y є гомеоморфізмом простору Х на Y, то індукований гомоморфізм f_* : π(Х, р) π(Y, f р) є ізоморфізмом при будь-якому виборі базисної точки р.

Доведення являє собою просту вправу на використання властивостей функції f_* , сформульовані в (4.5). Відображення

Х ^f Y ^f X

індукують гомоморфізми

π(Х, р) ^f_* π(Y, f р) ^{( f-1)}_* π(Х, р).

Але композиції f · f^-1 і f^-1· f є тотожніми відображеннями. Отже, такими є і гомоморфізми (f^-1· f)_* = f_*^-1 · f _*, (f · f^-1) = f · f_*^-1. Звідси слідує, що гомоморфізм f_* є ізоморфізмом на. Доведення завершене.

Отже, якщо лінійно зв’язні простори Х і Y гомоморфізми, то їх фундаментальні групи ізоморфні.

СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1. Кроуел Р. Введення в теорію вузлів. Р. Кроуел, Р. Фокс. – Москва: Мир. – 1967. – 348с.