Метод простых итераций
Пусть известно, что корень 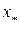 уравнения
уравнения 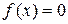 принадлежит отрезку
принадлежит отрезку 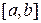 .
.
Методика решения задачи.
1. Уравнение 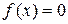 равносильным преобразованием привести к виду
равносильным преобразованием привести к виду 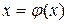 . Это преобразование может быть осуществлено различными путями, но для сходимости нужно обеспечить выполнение условия
. Это преобразование может быть осуществлено различными путями, но для сходимости нужно обеспечить выполнение условия 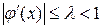 (
(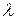 – некоторая константа). При этом задача сводится к нахождению абсциссы точки пересечения прямой
– некоторая константа). При этом задача сводится к нахождению абсциссы точки пересечения прямой 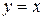 и кривой
и кривой 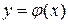 .
.
2. Задать начальное приближение 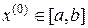 и малое положительное число
и малое положительное число 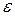 . Положить
. Положить 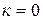 .
.
3. Вычислить следующее приближение
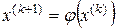 . (1)
. (1)
4. Если 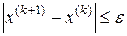 , итерации завершаются и
, итерации завершаются и 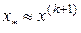 .
.
Если 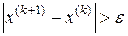 , положить
, положить 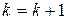 и перейти к п.3.
и перейти к п.3.
Преобразование уравнения 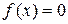 к равносильному виду
к равносильному виду 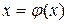 может быть выполнено неоднозначно. Рассмотрим универсальные практические приемы равносильного преобразования
может быть выполнено неоднозначно. Рассмотрим универсальные практические приемы равносильного преобразования 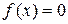 .
.
1. Уравнение 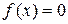 заменяется равносильным
заменяется равносильным 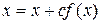 , где
, где 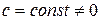 . Тогда, принимая правую часть этого уравнения за
. Тогда, принимая правую часть этого уравнения за 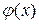 и раскрывая
и раскрывая 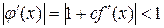 , получим условие
, получим условие
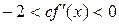 . (2)
. (2)
Таким образом, можно найти константу 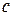 на отрезке
на отрезке 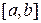 так, чтобы удовлетворялись неравенства (2). При этом надо стремиться получить такую постоянную
так, чтобы удовлетворялись неравенства (2). При этом надо стремиться получить такую постоянную 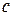 , которая бы больше отличалась от нуля, и тогда будет реализовываться более быстрая сходимость.
, которая бы больше отличалась от нуля, и тогда будет реализовываться более быстрая сходимость.
2. Уравнение 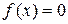 заменяется равносильным
заменяется равносильным 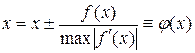 , где знак в правой части выбирается из условия
, где знак в правой части выбирается из условия 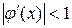 .
.
3. Из уравнения 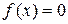 выражается
выражается 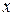 так, чтобы для полученного уравнения
так, чтобы для полученного уравнения 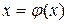 выполнялось условие сходимости
выполнялось условие сходимости 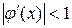 в окрестности искомого корня.
в окрестности искомого корня.
Пример 1. Найти корень уравнения 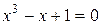 методом простых итераций с точностью
методом простых итераций с точностью 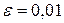 .
.
Решение.
Корень уравнения 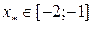 . Преобразуем уравнение к виду
. Преобразуем уравнение к виду 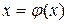 . Для этого запишем его сначала в форме
. Для этого запишем его сначала в форме 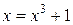 . Функция
. Функция 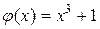 не удовлетворяет условию сходимости, так как
не удовлетворяет условию сходимости, так как 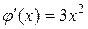 ,
, 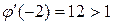 ,
, 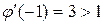 . Поэтому воспользуемся другим преобразованием.
. Поэтому воспользуемся другим преобразованием.
В результате получим 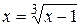 . Можно проверить, что
. Можно проверить, что 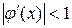 на отрезке
на отрезке 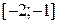 , то есть достаточное условие сходимости выполняется.
, то есть достаточное условие сходимости выполняется.
Зададим начальное приближение 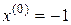 . Выполним расчеты по формуле (1):
. Выполним расчеты по формуле (1): 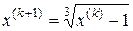 ,
, 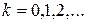
Результаты расчетов приведены в таблице 1.
Таблица 1.
| 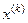
| 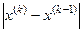
|
| -1 | - | |
| -1,2599 | 0,2599 | |
| -1,3123 | 0,0524 | |
| -1,3223 | 0,0100 |
Таким образом, 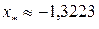 .
.
Пример 2. Найти корень уравнения 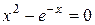 методом простых итераций с точностью
методом простых итераций с точностью 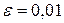 .
.
Решение.
Корень уравнения 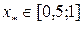 . Преобразуем исходное уравнение к виду
. Преобразуем исходное уравнение к виду 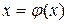 :
: 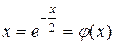 . Проверкой можно убедиться, что
. Проверкой можно убедиться, что 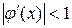 на отрезке
на отрезке 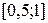 , то есть достаточное условие сходимости выполняется.
, то есть достаточное условие сходимости выполняется.
В качестве начального приближения выберем 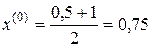 .
.
Выполним последовательные действия по формуле (3.7): 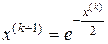 .
.
Результаты расчетов приведены в таблице 2.
Таблица 2.
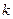
| 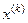
| 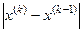
|
| 0,7500 | - | |
| 0,6873 | 0,0627 | |
| 0,7091 | 0,0218 | |
| 0,7015 | 0,0076 |
На третьей итерации выполнилось условие 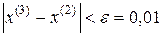 , поэтому процесс завершен. В качестве приближенного решения возьмем
, поэтому процесс завершен. В качестве приближенного решения возьмем 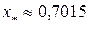 .
.
 2015-06-26
2015-06-26 138
138






